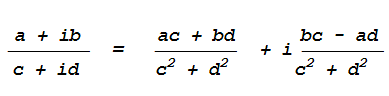
[Applications] [Matlab/Octave] [Self deconvolution] [Excess noise reduction by denominator addition] [Multiple sequential deconvolution] [Segmented deconvolution] [convdeconv function] [Live Script] [Interactive deconvolution in iSignal]
Fourier deconvolution is
the converse of Fourier convolution
in the sense that division is the converse of multiplication. If
you know that m times x equals
n, where m and n are known
but x is unknown, then x equals n
divided by m. Conversely if you know that m
convoluted with x equals n,
where m and n are known but x
is unknown, then x equals m deconvoluted
from n.
In practice, the deconvolution of one signal from another is
usually performed by point-by-point division of the two
signals in the Fourier domain, that is, dividing the Fourier
transforms of the two signals point-by-point and then
inverse-transforming the result. Fourier transforms are usually
expressed in terms of complex numbers, with real and imaginary
parts representing the sine and cosine parts. If the Fourier
transform of the first signal is a + ib, and the Fourier
transform of the second signal is c + id, then the ratio
of the two Fourier transforms is
by the rules for the division
of
complex numbers. Many computer languages will perform this
operation automatically when the two quantities divided are
complex.
Note: The word "deconvolution"
can have two meanings, which can lead to confusion. The Oxford
dictionary defines it as "A process of resolving something into
its constituent elements or removing complication in order to
clarify it", which in one sense applies to Fourier deconvolution.
But the same word is also sometimes used for the process of
resolving or decomposing a set of overlapping peaks into their
separate additive components by the technique of iterative least-squares curve fitting
of a proposed peak model to the data set. However, that process is
actually conceptually distinct from Fourier deconvolution,
because in Fourier deconvolution, the underlying peak shape is
unknown but the broadening function is assumed to be known;
whereas in iterative least-squares curve fitting it's just the
reverse: the peak shape must be known but the width of the
broadening process, which determines the width and shape of the
peaks in the recorded data, is unknown. Thus the term "spectral
deconvolution" is ambiguous: it might mean the Fourier
deconvolution of a response function from a spectrum, or it might
mean the decomposing of a spectrum into its separate additive peak
components. These are different processes; don't get them
confused.
The practical
significance of Fourier deconvolution in signal processing
is that it can be used as a computational way to reverse the
result of a convolution occurring in the physical domain, for
example, to reverse the signal distortion effect of an electrical
filter or of the finite resolution of a spectrometer. In some
cases the physical convolution can be measured experimentally by
applying a single spike impulse ("delta") function to the input of
the system, then that data used as a deconvolution vector.
Deconvolution can also be used to determine the form of a
convolution operation that has been previously applied to a
signal, by deconvoluting the original and the convoluted signals.
These two types of application of Fourier deconvolution are shown
in the two figures below.
Fourier deconvolution is used here to remove the distorting influence of an exponential tailing response function from a recorded signal (Window 1, top left) that is the result of an unavoidable RC low-pass filter action in the electronics. The response function (Window 2, top right) must be known and is usually either calculated on the basis of some theoretical model or is measured experimentally as the output signal produced by applying an impulse (delta) function to the input of the system. The response function, with its maximum at x=0, is deconvoluted from the original signal . The result (bottom, center) shows a closer approximation to the real shape of the peaks; however, the signal-to-noise ratio is unavoidably degraded compared to the recorded signal, because the Fourier deconvolution operation is simply recovering the original signal before the low-pass filtering, noise and all. (Matlab/Octave script)
Note that this
process has an effect that is visually similar to resolution enhancement,
although the later is done without specific knowledge of the
broadening function that caused the peaks to overlap.
A different application of Fourier deconvolution is to reveal the nature of an unknown data transformation function that has been applied to a data set by the measurement instrument itself. In this example, the figure in the top left is a uv-visible absorption spectrum recorded from a commercial photodiode array spectrometer (X-axis: nanometers; Y-axis: milliabsorbance). The figure in the top right is the first derivative of this spectrum produced by an (unknown) algorithm in the software supplied with the spectrometer. The objective here is to understand the nature of the differentiation/smoothing algorithm that the instrument's software uses. The signal in the bottom left is the result of deconvoluting the derivative spectrum (top right) from the original spectrum (top left). This therefore must be the convolution function used by the differentiation algorithm in the spectrometer's software. Rotating and expanding it on the x-axis makes the function easier to see (bottom right). Expressed in terms of the smallest whole numbers, the convolution series is seen to be +2, +1, 0, -1, -2. This simple example of "reverse engineering" would make it easier to compare results from other instruments or to duplicate these result on other equipment.
When applying Fourier
deconvolution to experimental data, for example to remove the
effect of a known broadening or low-pass filter operator caused by
the experimental system, there are four serious problems that
limit the utility of the method:
(1) the convolution occurring in the physical domain might not be accurately modeled by a mathematical convolution;
(2) the width of the convolution - for example the time constant of a low-pass filter operator or the shape and width of a spectrometer slit function - must be known, or at least adjusted by the user to get the best results;
(3) a serious signal-to-noise degradation commonly occurs; any noise added to the signal by the system after the convolution by the broadening or low-pass filter operator will be greatly amplified when the Fourier transform of the signal is divided by the Fourier transform of the broadening operator, because the high frequency components of the broadening operator (the denominator in the division of the Fourier transforms) are typically very small, with some individual components often of the order of 10-12 or 10-15, resulting a huge amplification of those particular frequencies in the resulting deconvoluted signal, which is called "ringing". (See the Matlab/Octave code example at the bottom of this page). The problem can be reduced either by low-pass filtering (smoothing). Smoothing or filtering reduces the amplitude of the highest-frequency components.
You can see the amplification of high frequency noise happening in the example in the first example above. On the other hand, this effect is not observed in the second example, because in that case the noise was present in the original signal, before the convolution performed by the spectrometer's derivative algorithm. The high frequency components of the denominator in the division of the Fourier transforms are typically much larger than in the previous example, avoiding the noise amplification and divide-by-zero errors, and the only post-convolution noise comes from numerical round-off errors in the math computations performed by the derivative and smoothing operation, which is always much smaller than the noise in the original experimental signal.
In many cases, the width of the physical convolution is not known
exactly, so the deconvolution must be adjusted empirically to
yield the best results. Similarly, the width of the final smooth
operation must also be adjusted for best results. The result will
seldom be perfect, especially if the original signal is noisy, but
it is often a better approximation to the real underlying signal
than the recorded data without deconvolution.
As a method for peak sharpening, deconvolution can be
compared to the derivative
peak sharpening method described earlier or to the power method, in
which the raw signal is simply raised to some positive power n.
Matlab
and Octave have a built-in function for Fourier
deconvolution: deconv. An example
of its application is shown below: the vector yc (line 6)
represents a noisy rectangular pulse (y) convoluted with a
transfer function c before being measured. In line 7, c
is deconvoluted from yc, in an attempt to recover the
original y. This requires that the transfer function c
be known. The rectangular signal pulse is recovered in the lower
right (ydc), complete with the noise that was present in
the original signal. The Fourier deconvolution reverses not
only the signal-distorting effect of the convolution by the
exponential function, but also its low-pass noise-filtering
effect. As explained above, there is significant amplification of
any noise that is added after the convolution by the
transfer function (line 5). This script demonstrates that there is
a big difference between noise added before the
convolution (line 3), which is recovered unmodified by the Fourier
deconvolution along with the signal, and noise added after
the convolution (line 6), which is amplified compared to that in
the original signal. Execution time: 0.03 seconds in Matlab; 0.3
seconds in Octave. Download this
script.
x=0:.01:20;
y=zeros(size(x));
% Create a rectangular function y, 200 points wide
y(900:1100)=1;
%
Noise added before
the convolution
y=y+.01.*randn(size(y));
% exponential trailing
convolution function, c
c=exp(-(1:length(y))./30);
% Create exponential trailing rectangular
% function, yc
yc=conv(y,c,'full')./sum(c);
%
Optional noise added after the convolution
%
yc=yc+.01.*randn(size(yc));
% Attempt to recover y by deconvoluting c from yc
ydc=deconv(yc,c).*sum(c);
% The sum(c2) is included simply to scale
the
% amplitude of the result to match the original y.
% Plot all the steps in separate subplots
subplot(2,2,1); plot(x,y); title('original y');
subplot(2,2,2); plot(x,c);title('c'); subplot(2,2,3);
plot(x,yc(1:2001)); title('yc'); subplot(2,2,4);
plot(x,ydc);title('recovered y')
Click here for
a simple explicit example of Fourier convolution and
deconvolution, for a small 9-element vector, with the vectors
printed out at each stage.
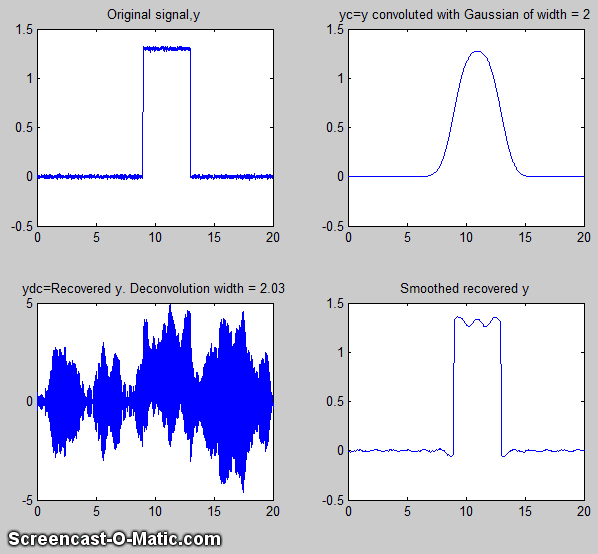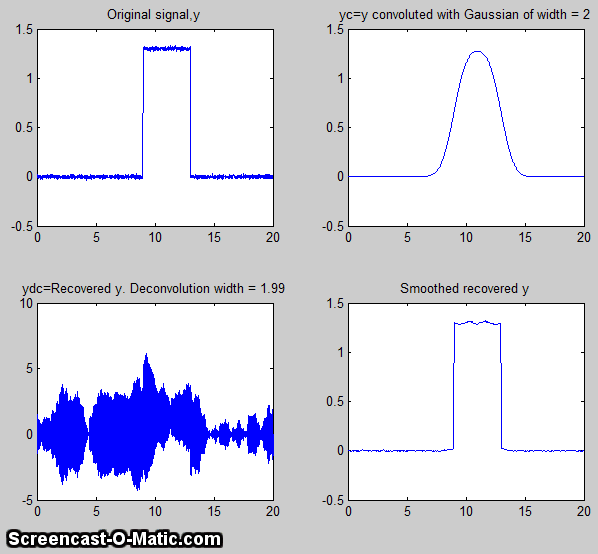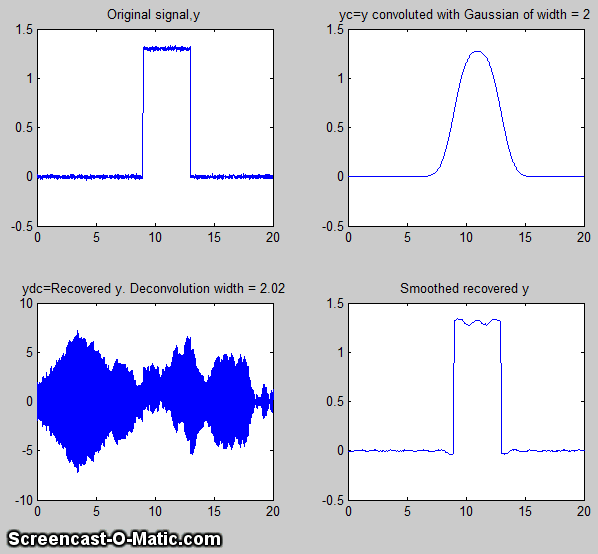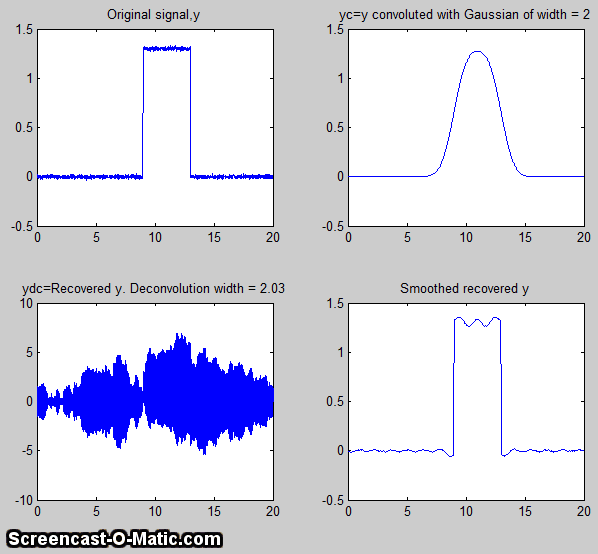The script DeconvDemo3.m is similar to the above,
except that it demonstrates Gaussian Fourier convolution
and deconvolution of the same rectangular pulse, utilizing the
fft/ifft formulation just described. The animated screen graphic is
shown on the left, demonstrating the effect of changing the
deconvolution width. The raw deconvoluted signal in this example
(bottom left quadrant) is extremely noisy, but that noise is mostly
"blue" (high frequency)
noise that is easily reduced by a little smoothing. As you can see in both of the
animated examples here, deconvolution works best when the
deconvolution width exactly matches the width of the convolution
that the observed signal has been subject to; the further off you
are, the worse will be the wiggles and other signal artifacts. In
practice, you have to try several different deconvolution widths to
find the one that results in the smallest wiggles, which of
course becomes harder to see if the signal is very noisy.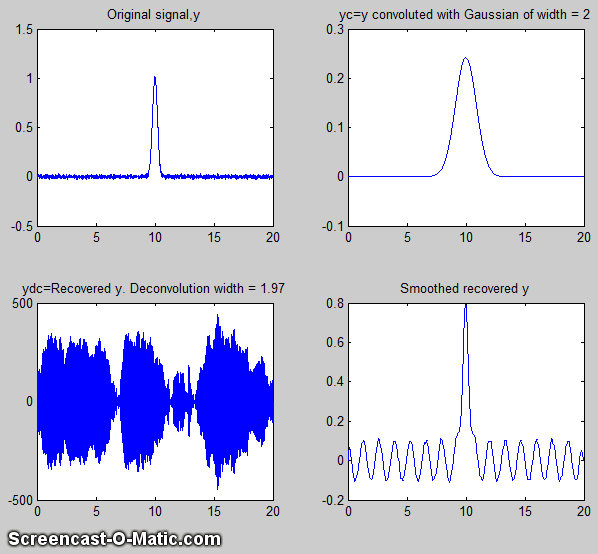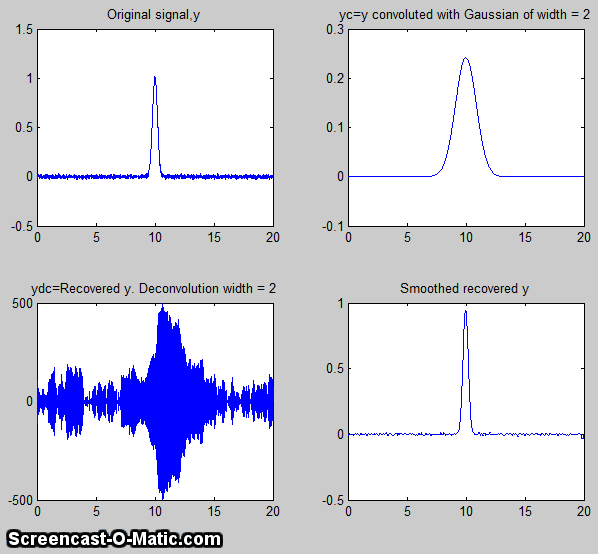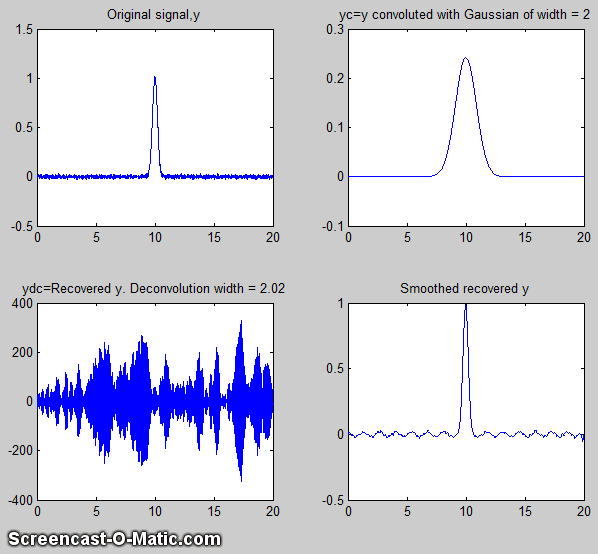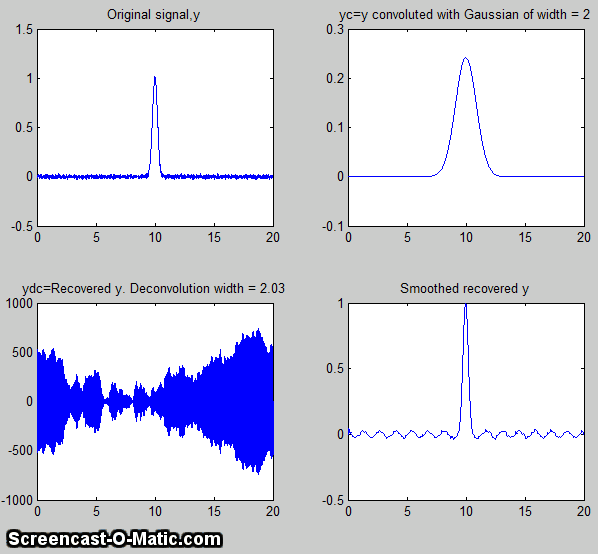
attempt to
recover the original peak width. Typically this would be applied to
a signal containing multiple overlapping peaks, in an attempt to
sharpen the peaks to improve the resolution. Note that in this
example the deconvolution width must be within 1% of the
deconvolution width. In general, the wider the physical convolution
width relative to the signal, the more accurately the deconvolution
width must be matched the physical convolution width.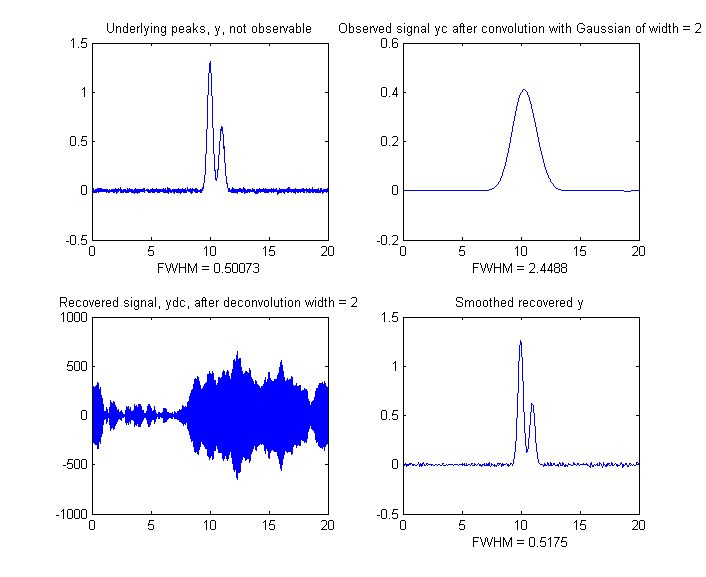
(shown on the
left) shows an example with two closely-spaced underlying
peaks of equal width that are completely unresolved in the
observed signal, but are recovered with their 2:1 height ratio
intact in the deconvoluted and smoothed result. DeconvDemo6.m is that same except that
the underlying peaks are Lorentzian.
This image shows the widths of the peaks (as full width at half
maximum) in the captions, showing that the width of the deconvoluted
peaks (lower right quadrant) are actually slightly larger than in
the (unobserved) underlying peaks (upper left quadrant) either
because of imperfect deconvolution or because of the broadening
effects of the smoothing needed to reduce the high frequency noise.
(Note that all these scripts require functions than can be
downloaded from http://tinyurl.com/cey8rwh).
However,
the noise remaining in the deconvoluted signal is "blue"
(high-frequency weighted) and so is easily reduced by smoothing and
has less effect on least-square fits than does white noise. (For a
greater challenge, try more noise in line 6 or a bad guess of time
constant ('tc') in line 7). To plot the recovered signal overlaid
with underlying signal: plot(xx,uyy,xx,yydc). To plot the observed
signal overlaid with with underlying signal: 
ydc=ifft(fft(y)./(fft(df))).*sum(df)
Here is the
code for the case where the denominator addition is a
constant:
D=fft(df)+DA.*max(fft(df));
ydcDA=ifft(fft(y)./D).*sum(df);
where y
is the original signal, D is the denominator, df is the
deconvolution function and FDA is the fractional
denominator addition. The addition is scaled to the maximum
value of the fft of the deconvolution function df so
that the quantity added will adjust to the varying amplitudes
of different experimental signals.
An alternative
is to add a constant only to those members of the
denominator below a specified threshold, e.g. using the
"no lower than" function nlt(a,b):
D=nlt(fftc,FDA.*0.01.*max(fftc));
ydcDA=ifft(fft(y)./D).*sum(df);
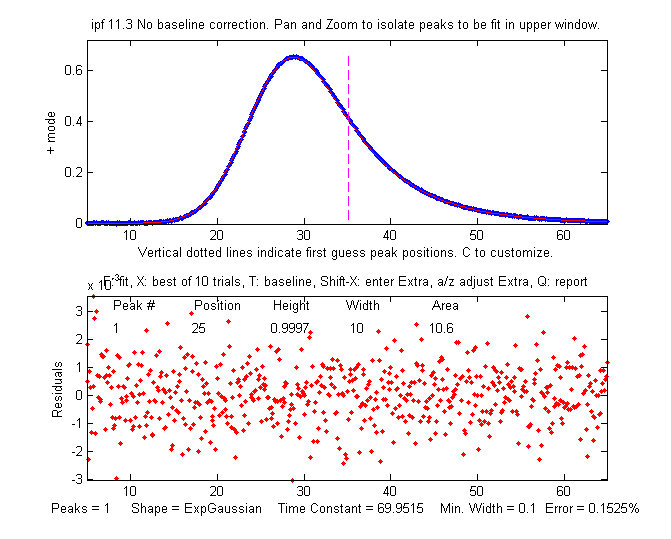
Deconvolution for peak
area measurements. Measuring the areas under peaks is a common
requirement in quantitative analysis, but it works only if there
is sufficient separation between peaks. Because deconvolution
sharpens peaks but does not change the area under them, it can
be used to improve the measurement of the areas of overlapping
peaks. In the Matlab script GLSDPerpDropDemo16.m, the areas of a group of three
partially overlapping peaks is measured, by the perpendicular
drop method, before and after peak sharpening by Fourier
self-deconvolution. The measurements are repeated with random
peak height, to test how the peak overlap interferes with
precise area measurement. After sixteen trials with randomized
peak heights, the true peak area are plotted against the
measured areas, and the R2 values for each case are
compared before and after deconvolution. The results are
summarized on this
PDF file. Conclusion: in every case, from the "easiest" to
the most challenging, deconvolution yields the best results.
tstep=(endt-startt)/NumSegments;
tc=startt:tstep:endt;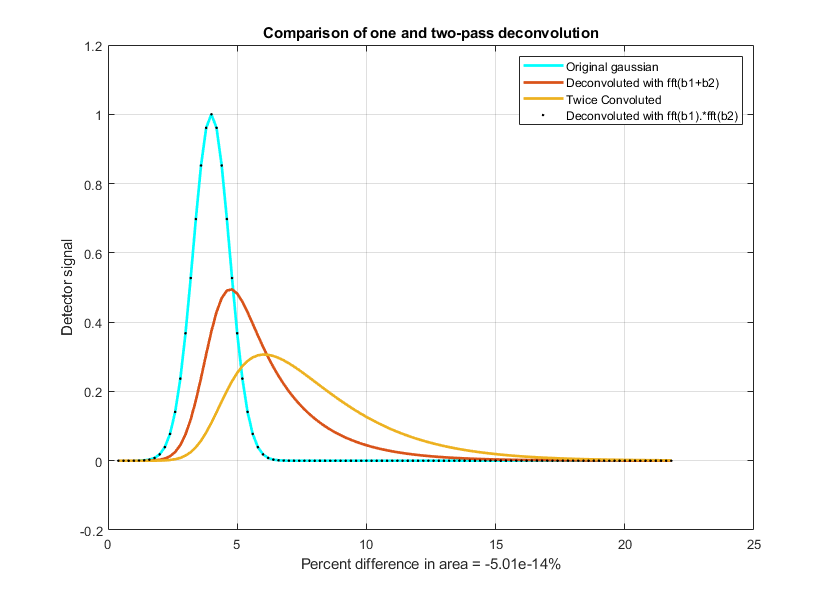
In cases where the signal may have been
subject to two or more sequential convolutions, as described in
the previous section,
the reversal of that effect requires multiple sequential
deconvolutions and cannot be undone
Live script for self-deconvolution.
DeconvoluteData.mlx can
perform Fourier self-deconvolution on you own data stored in
disk. Clicking the Open data file button in line 1
opens a file browser, allowing you to navigate to your data
file in .csv or .xlsx format. (The script assumes that your
x,y data are in the first two columns; you can change that in
lines 13 and 14). In the case shown here, the data file is a
portion of the IR spectrum of Heptene, 'HepteneTestData.csv',
shown as the 'file' variable in the workspace. The startpc and endpc sliders
in lines 9 and 10 allow you to select which portion of the
data range to process, from 0% to 100% of the total range of
the data file.
The PeakShape drop-down menu in line 17 selects the convolution function shape (in this case, a Gaussian-Lorentzian blend) and for that shape the PCGaussian slider in the next line allows selection of the percent Gaussian. The dw slider in line 21 controls the deconvolution half-width, the DA slider in line 23 controls the percent denominator addition. Smoothing, by Fourier filtering, is controlled by the FrequencyCutoff and CutOffRate in lines 25 and 27. All variables are accessible in the Matlab workspace; the final signal is 'syDA'.
Click the FrequencySpectra
check box in line 4 to view the frequency spectra. Click
the PlotAllSteps check box in line 5 to
view all the steps leading up to the the final
result. To view the figures to the right as shown
below, right-click on the right-hand panel and
select "Disable synchronous scrolling".
Self-deconvolution
sharpening of the IR spectrum of Heptene, 'HepteneTestData.csv'
In iSignal version 8.3, and its Octave
version, the downloadable interactive multipurpose
signal processing Matlab function, you can press Shift-V to
display the menu
of
Fourier convolution and deconvolution operations that allow you to convolute or to
deconvolute a Gaussian, Lorentzian or exponential function. It
will ask you for the initial width or time constant of
the deconvolution function (Vwidth, in X units), then you
can use the 3 and 4 keys
to decrease or increase the width by 10% (or Shift-3 and Shift-4 to
adjust
by 1%).Here's an application to a real
experimental signal. The denominator addition (to suppress
ringing and noise) is controlled by the 5
and 6 keys.
In this example, the
original signal is shown as the dotted green line and the
results of deconvoluting it with a Lorentzian
deconvolution function is shown as the blue line. The
deconvolution width was adjusted as large as possible without
causing significant negative dips between the peaks, which for
many types of experimental data, would be non-physical.
(Recall that the mathematics of the deconvolution operation is
structured so that the area
under the peaks remains unchanged, even though the
widths are reduced and the heights are increased). Several of
the peaks shown in the zoomed-in close-up in the upper panel
have shoulders that are resolved into distinct peaks, allowing
their peak positions to be measured more accurately.
Fortunately, the amplitude of those revealed peaks is greater
than the small amount of noise remaining in the signal (thanks
to the good signal-to-noise ratio of the original signal).
Revised May, 2023. This page is part of "A Pragmatic Introduction to Signal Processing", created and maintained by Prof. Tom O'Haver , Department of Chemistry and Biochemistry, The University of Maryland at College Park. Comments, suggestions and questions should be directed to Prof. O'Haver at toh@umd.edu.