[Model
errors] [Number of
peaks] [Peak
width] [Background
correction] [Random noise]
[Iterative fitting errors]
[Exponential broadening]
[Effect of smoothing]
Iterative curve fitting is often used to measure the
position, height, and width of peaks in a signal, especially
when they overlap significantly. There are four major sources
of error in measuring these peak parameters by iterative curve
fitting: model
errors, background
correction, random
noise, and iterative
fitting errors. This section makes use of the
downloadable peakfit.m function.
Instructions are here or
type "help peakfit". (Once you have peakfit.m in youjr path,
you can simply copy and paste, or drag and drop, any of the
following single-line or multi-line code examples into the
Matlab or Octave editor or into the command line and press Enter
to execute it).
a. Model errors.
Peak shape. If you have the wrong model for your
peaks, the results can not be expected to be accurate; for
instance, if your actual peaks are Lorentzian in shape, but
you fit them with a Gaussian model, or vice versa. For example,
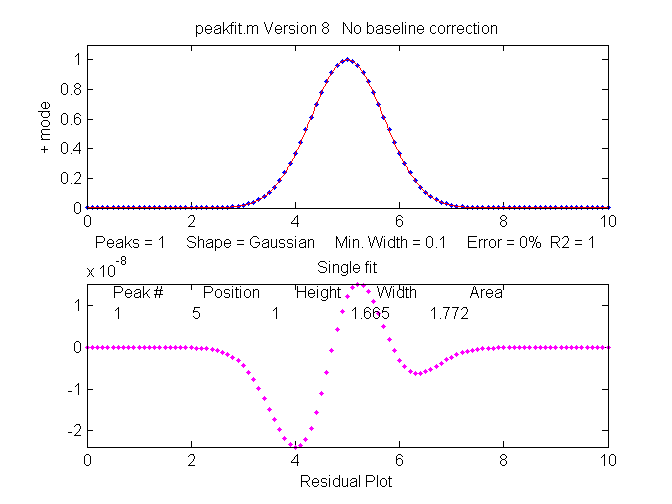
a single isolated Gaussian peak at x=5, with a height of 1.000
fits a Gaussian model virtually perfectly, using the Matlab
user-defined peakfit
function, as shown on the right. (The 5th input argument for
the peakfit function specifies the shape of peaks to be used
in the fit; "1" means Gaussian).
>>
x=[0:.1:10];y=exp(-(x-5).^2);
>> [FitResults,MeanFitError]=peakfit([x' y'],5,10,1,1)
Peak#
Position
Height
Width Area
FitResults =
1
5
1
1.6651 1.7725
MeanFitError
= R2=
7.8579e-07
1
The "FitResults" are, from left to right, peak number,
peak position, peak height, peak width, and peak area. The
MeanFitError, or just "fitting error", is the square root
of the sum of the squares of the differences between t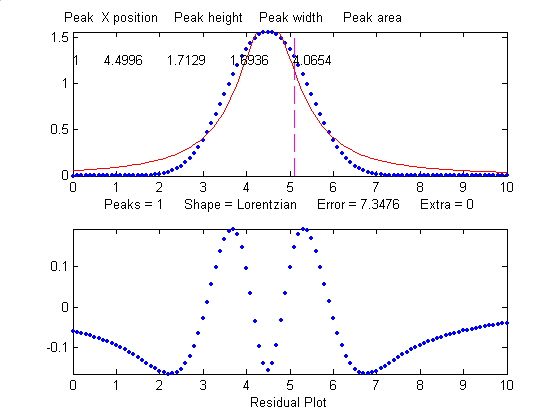 he data and the
best-fit model, as a percentage of the maximum signal in the
fitted region. R2 is the "R-squared" or coefficient of
determination, which is exactly 1 for a perfect fit. Note the
good agreement of the area measurement (1.7725) with the theoretical area
under the curve of exp(-x2), which turns out
to be the square
root of pi, or
about 1.7725....
he data and the
best-fit model, as a percentage of the maximum signal in the
fitted region. R2 is the "R-squared" or coefficient of
determination, which is exactly 1 for a perfect fit. Note the
good agreement of the area measurement (1.7725) with the theoretical area
under the curve of exp(-x2), which turns out
to be the square
root of pi, or
about 1.7725....
But this same peak, when fit with
the incorrect model (a Logistic model, peak shape
number 3), gives a fitting error of 1.4% and height and width
errors of 3% and 6%, respectively. However, the
peak area error is only 1.7%, because the height and
width errors partially cancel out. So you don't have to have a
perfect model to get a decent area measurement.
>> [FitResults,MeanFitError]=peakfit([x'
y'],5,10,1,3)
Peak#
Position
Height
Width
Area
FitResults =
1
5.0002
0.96652
1.762
1.7419
MeanFitError =1.4095
When fit with an even more
incorrect Lorentzian model (peak shape 2, shown on
the right), this peak gives a 6% fitting error and height,
width and area errors of 8%, 20%, and 17%, respectively.
>> [FitResults,MeanFitError]=peakfit([x'
y'],5,10,1,2)
FitResults =
Peak#
Position
Height
Width Area
1
5
1.0876
1.3139
2.0579
MeanFitError =5.7893
But, practically speaking,
Gaussian and Lorentzian shapes are so visually distinct that
it's unlikely that your estimate of a model will be that far
off. Real peak shapes are often some unknown combination of
peak shapes, such as Gaussian with a little Lorentzian or vice
versa, or some slightly asymmetrical modification of a
standard symmetrical shape. So if you use an available model
that is at least close to the actual shape, the
parameters errors may not be so bad and may in fact be better
than other measurement methods.
So clearly the larger the fitting
errors, the larger are the parameter errors, but the parameter
errors are of course not equal
to the fitting error (that would just be too easy). Also,
it's clear that the peak height and width are the
parameters most susceptible to errors. The peak positions, as you can see
here, are measured accurately even if the model is way wrong,
as long as the peak is symmetrical and not highly overlapping
with other peaks.
A good fit is not by itself
proof that the shape function you have chosen is the correct
one; in some cases the wrong function can give a fit
that looks perfect. For example, this fit of a real data set
to a 5-peak Gaussian model has a low percent fitting error and
the residuals look random - usually an indicator of a good
fit. But in fact in this case the model is wrong; that
data came from an experimental domain where the underlying
shape is fundamentally non-Gaussian but in some cases can look
very like a Gaussian. As another example, a data set
consisting of peaks with a Voigt profile
peak shape can be fit with a weighted
sum of a Gaussian and a Lorentzian almost as well as an
with an actual Voigt model, even
though those models are not the same mathematically;
the difference in fitting error is so small that it would
likely be obscured by the random
noise if it were a real experimental signal. The same
thing can occur in sigmoidal signal shapes: a pair of simple
2-parameter logistic functions seems to fit this example data pretty well,
with a fitting error of less than 1%; you would have no reason
to doubt the goodness of fit unless the random noise is low
enough so you can see that the residuals are wavy.
Alternatively, a 3-parameter logistic (Gompertz
function) fits much better, and
the residuals are random, not wavy. In such cases you can not
depend solely on what looks like a good fit to
determine whether the fit is model is optimum; sometimes you
need to know more about the peak shape expected in that kind
of experiment, especially if the data are noisy. At best, if
you do get a good fit with random non-wavy residuals, you can
claim that the data are consistent with the
proposed model. Note: with the peakfit.m function, you can
extract the residuals as a vector by using the syntax
[FitResults,GOF,baseline,coeff,residual,xi,yi]=peakfit(....
Sometimes the accuracy of the
model is not so important. In quantitative
analysis applications, where the peak height or areas
measured by curve fitting is used only to determine the
concentration of the substance that created the peak by
constructing a calibration
curve, using laboratory prepared standards solutions of
known concentrations, the necessity of using the exact peak
model is lessened, as long as the shape of the unknown peak is
constant and independent of concentration. If the wrong
model shape is used, the R2 for
curve fitting will be poor (much less than 1.000) and
the peak heights and areas measured by curve fitting will be
inaccurate, but the error will be exactly the same for
the unknown samples and the known calibration standards, so
the error will cancel out and, as a result, the R2
for the calibration curve can be very high (0.9999 or
better) and the measured concentrations will be no less
accurate than they would have been with a perfect peak shape
model. Even so, it's useful to use as accurate a model
peak shape as possible, because the R2
for curve fitting will work better as a warning indicator if
something unexpected goes wrong during the analysis (such as
an increase in the noise or the appearance of an interfering
peak from a foreign substance). See PeakShapeAnalyticalCurve.m
for a Matlab/Octave demonstration.
Number of peaks. Another
source
of model error occurs if you have the wrong number of peaks in your
model, for example if the signal actually has  two peaks
but you try to fit it with only one peak. In the example
below, a line of Matlab code generates a simulated signal with
of two Gaussian peaks at x=4 and x=6 with peaks heights of
1.000 and 0.5000 respectively and widths of 1.665, plus random
noise with a standard deviation 5% of the height of the
largest peak (a signal-to-noise ratio of 20):
two peaks
but you try to fit it with only one peak. In the example
below, a line of Matlab code generates a simulated signal with
of two Gaussian peaks at x=4 and x=6 with peaks heights of
1.000 and 0.5000 respectively and widths of 1.665, plus random
noise with a standard deviation 5% of the height of the
largest peak (a signal-to-noise ratio of 20):
>>x=[0:.1:10];y=exp(-(x-6).^2)+.5*exp(-(x-4).^2)+.05*randn(size(x));
In a real experiment you would not
usually know the peak positions, heights, and widths; you
would be using curve fitting to measure those parameters.
Let's assume that, on the basis of previous experience or some
preliminary trial fits, you have established that the optimum
peak shape model is
Gaussian, but you don't know for sure how many peaks are in
this group. If you start out by fitting this signal with a single-peak Gaussian
model, you get:
>>
[FitResults,MeanFitError]=peakfit([x' y'],5,10,1,1)
FitResults
Peak#
Position Height
Width Area
1
5.5291 0.86396
2.9789 2.7392
MeanFitError = 10.467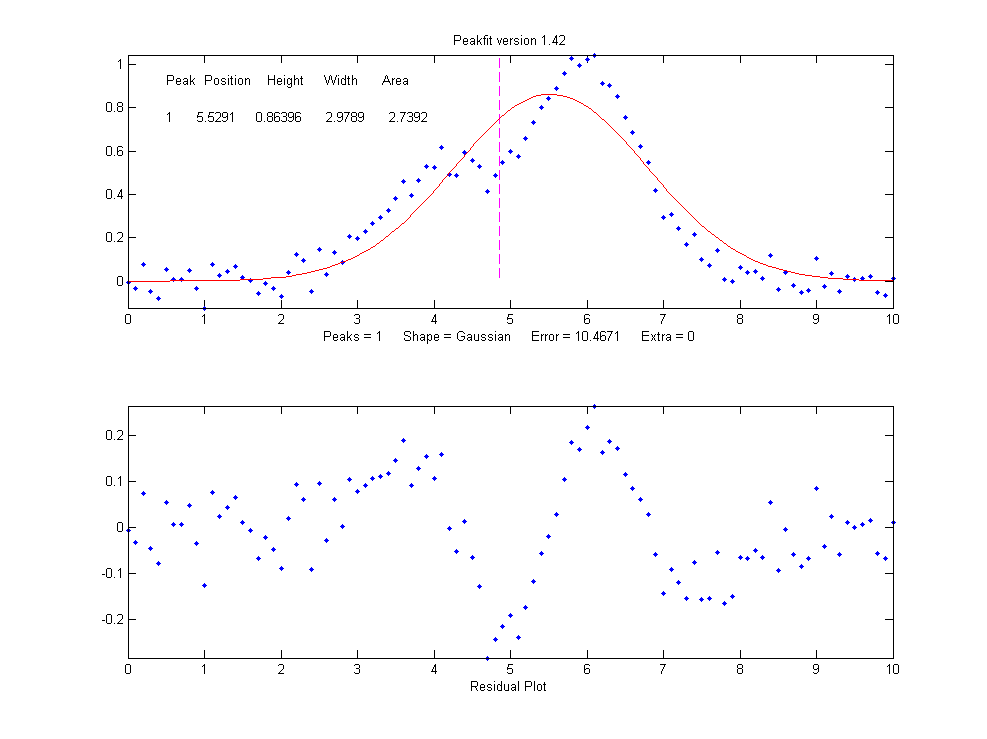
The residual plot shows a "wavy"
structure that's visible in the random scatter of points due
to the random noise in the signal. This means that the fitting
error is not limited by the random noise; it is a clue that
the model is not quite right.
But a fit with two peaks yields much
better results (The 4th input argument for the
peakfit function specifies the number of peaks to be used in
the fit).
>> [FitResults,MeanFitError]=peakfit([x'
y'],5,10,2,1)
FitResults =
Peak# Position
Height Width Area
1
4.0165
0.50484
1.6982
0.91267
2
5.9932 1.0018
1.6652 1.7759
MeanFitError =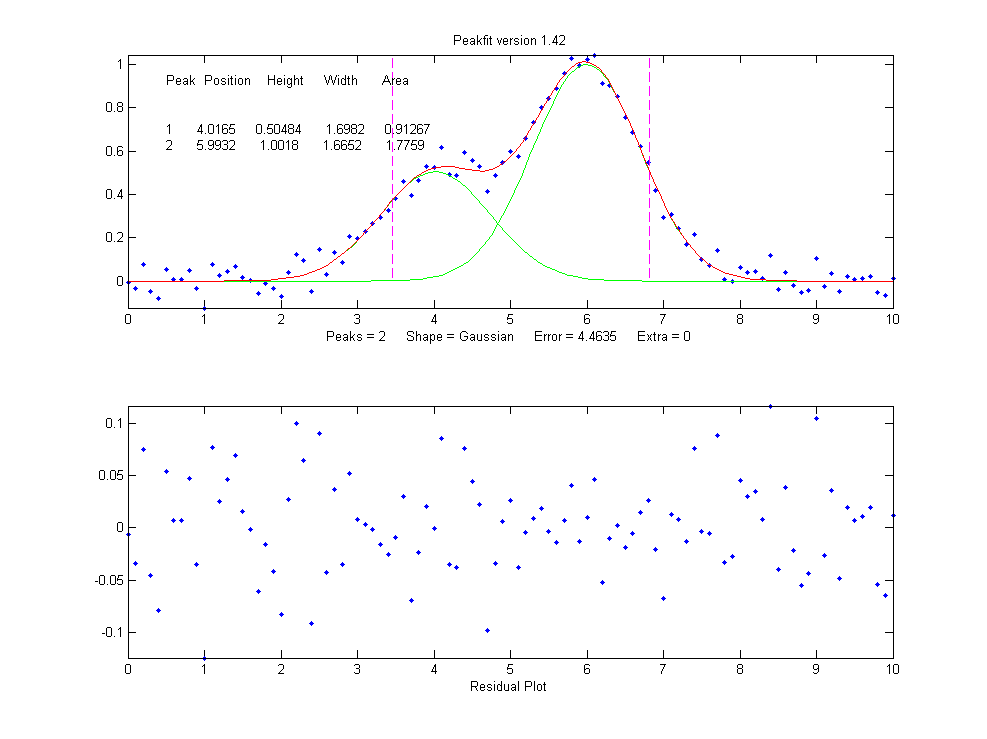 4.4635
4.4635
Now the residuals have a random
scatter of points, as would be expected if the signal is
accurately fit except for the random noise. Moreover, the
fitting error is much lower (less that half) of the error with
only one peak. In fact, the fitting error is just about what
we would expect in this case based on the 5% random noise in
the signal (estimating the relative standard deviation of the
points in the baseline visible at the edges of the signal).
Because this is a simulation in which we know beforehand the
true values of the peak parameters (peaks at x=4 and x=6 with
peaks heights of 1.0 and 0.50 respectively and widths of
1.665), we can actually calculate the parameter errors (the
difference between the real peak positions, heights, and
widths and the measured values). Note that they are quite
accurate (in this case within about 1% relative on the peak
height and 2% on the widths), which is actually better than
the 5% random noise in this signal because of the averaging
effect of fitting to multiple data points in the signal.
But if going from one peak to two
peaks gave us a better fit, why not go to three peaks? If
there were no noise in the data, and if the underlying peak
shape were perfectly matched by the model, then the fitting
error would have already been essentially zero with two model
peaks, and adding a third peak to the model would yield a
vanishingly small height for that third peak. But in our
examples here, as in real data, there is always some random
noise, and the result is that the third peak height will not
be zero. Changing the number of peaks to three gives these
results:
>> [FitResults,MeanFitError]=peakfit([x'
y'],5,10,3,1)
FitResults =
Peak# Position
Height Width Area
1 4.0748
0.51617 1.7874 0.98212
2 6.7799
0.089595 2.0455 0.19507
3 5.9711
0.94455 1.53 1.5384
MeanFitError =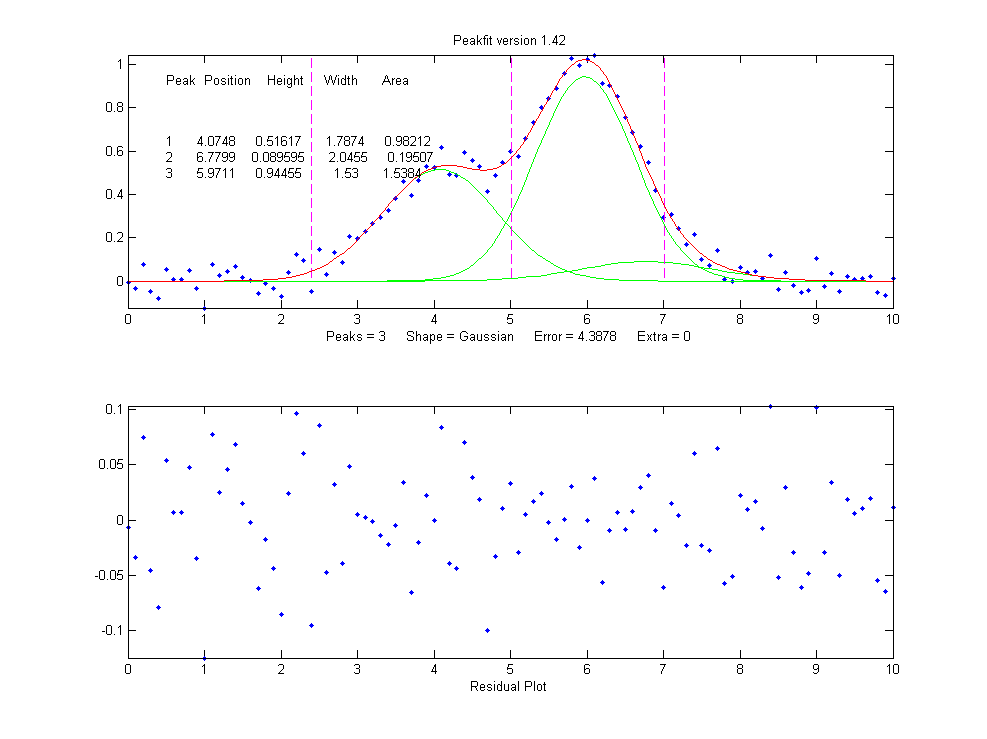 4.3878
4.3878
The fitting
algorithm has now tried to fit an additional low-amplitude
peak (numbered peak 2 in this case) located at x=6.78. The
fitting error is actually lower that for the 2-peak fit, but
only slightly lower, and the residuals are no less
visually random that with a 2-peak fit. So,
knowing nothing else, a 3-peak fit might be rejected on that
basis alone. In fact, there is a serious downside to fitting
more peaks than are actually present in the signal: it
increases the parameter measurement errors of the peaks that
are actually present. Again, we can prove this because we know
beforehand the true values of the peak parameters: clearly the
peak positions, heights, and widths of the two real peaks than
are actually in the signal (peaks 1 and 3) are significantly
less accurate than those of the 2-peak fit.
Moreover, if we repeat that fit
with the same signal
but with a different
sample of random noise (simulating a repeat measurement of a
stable experimental signal in the presence or random noise),
the additional third peak in the 3-peak fit will bounce around
all over the place (because the third peak is actually fitting
the random noise,
not an actual peak in the signal).
>> x=[0:.1:10];
>>
y=exp(-(x-6).^2)+.5*exp(-(x-4).^2)+.05*randn(size(x));
>> [FitResults,MeanFitError]=peakfit([x' y'],5,10,3,1)
FitResults =
Peak#
Position Height
Width Area
1
4.115
0.44767
1.8768 0.89442
2
5.3118 0.09340
2.6986 0.26832
3
6.0681
0.91085
1.5116 1.4657
MeanFitError = 4.4089
With this new set of data, two of
the peaks (numbers 1 and 3) have roughly the same position,
height, and width, but peak number 2 has changed substantially
compared to the previous run. Now we have an even more
compelling reason to reject the 3-peak model: the 3-peak
solution is not stable.
And because this is a simulation in which we know the right
answers, we can verify that the accuracy of the peak heights
is substantially poorer (about 10% error) than expected with
this level of random noise in the signal (5%). If we were to
run a 2-peak fit on the same new data, we get much better
measurements of the peak heights.
>> [FitResults,MeanFitError]=peakfit([x'
y'],5,10,2,1)
FitResults =
Peak# Position Height
Width
Area
1
4.1601
0.49981 1.9108 1.0167
2
6.0585
0.97557 1.548
1.6076
MeanFitError = 4.4113
If this is repeated several times,
it turns out that the peak parameters of the peaks at x=4
and x=6 are, on average, more accurately measured by the
2-peak fit. In practice, the best way to evaluate a proposed
fitting model is to fit several repeat measurements
of the same signal (if that is practical experimentally) and
to compute the standard deviation of the peak parameter
values.
In real experimental
work, of course, you usually don't know the
right answers beforehand, so that's why it's important
to use methods that work well when you do know.
The real data example
mentioned above was fit with a succession of 2, 3, 4 and 5 Gaussian
models, until the residuals became random. Beyond that
point, there is little to be gained by adding more peaks
to the model. Another way to determine the minimum
number of models peaks needed is to plot the fitting
error vs the number of model peaks; the point at which
the fitting error reaches a minimum, and increases
afterward, would be the fit with the "ideal
combination of having the best fit without
excess/unnecessary terms". The
Matlab/Octave function testnumpeaks.m
(R = testnumpeaks(x, y, peakshape, extra,
NumTrials, MaxPeaks))
applies this idea by fitting the x,y data to a series of
models of shape peakshape containing
1 to MaxPeaks
model peaks. The correct number of
underlying peaks is either the model with the lowest fitting
error, or, if two or more models have about the same fitting
error, the model with the least number of peaks. The
Matlab/Octave demo script NumPeaksTest.m
uses this function with noisy computer-generated signals
containing a user-selected 3, 4, 5 or 6 underlying
peaks. With very noisy data,
however, the technique is not always reliable.
Peak width constraints.
Finally, there is one more thing that we can do that
might improve the peak parameter measurement accuracy, and it
concerns  the
peak widths. In all the above simulations, the basic
assumption that all
the peak parameters were unknown and independent of one
another. In some types of measurements, however, the peak
widths of each group of adjacent peaks are all expected to be
equal to each other, on the basis of first principles or
previous experiments. This is a common situation in analytical
chemistry, especially in atomic spectroscopy and in
chromatography, where the peak widths are determined largely
by instrumental factors.
the
peak widths. In all the above simulations, the basic
assumption that all
the peak parameters were unknown and independent of one
another. In some types of measurements, however, the peak
widths of each group of adjacent peaks are all expected to be
equal to each other, on the basis of first principles or
previous experiments. This is a common situation in analytical
chemistry, especially in atomic spectroscopy and in
chromatography, where the peak widths are determined largely
by instrumental factors.
In the current simulation, the
true peaks widths are in fact both equal to 1.665, but all the
results above show that the measured
peak widths are close but not quite equal, due to random noise
in the signal. The unequal peak widths are a consequence of
the random noise, not real differences in peak width. But we
can introduce an equal-width
constraint into the fit by using peak shape 6 (Equal-width
Gaussians) or peak shape 7 (Equal-width Lorentzians). Using
peak shape 6 on the same set of data as the previous example:
>> [FitResults,MeanFitError]=peakfit([x'
y'],5,10,2,6)
FitResults =
Peak#
Position Height
Width Area
1 4.0293 0.52818
1.5666 0.8808
2 5.9965
1.0192 1.5666 1.6997
MeanFitError =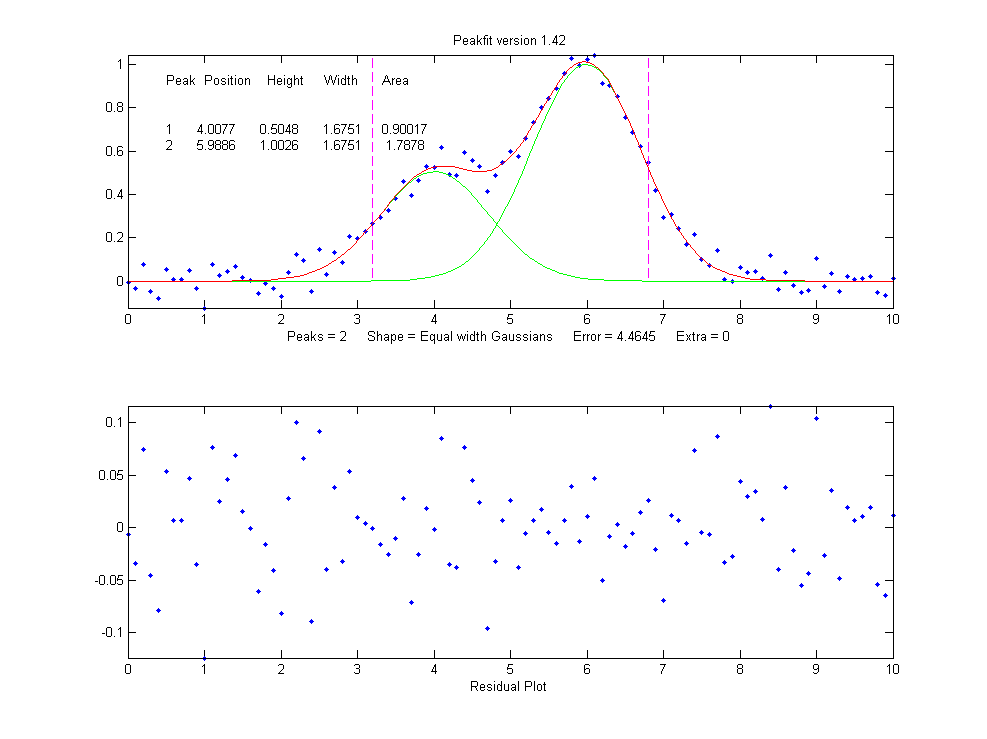 4.5588
4.5588
This "equal width" fit forces all the peaks within one group
to have exactly the same width, but that width is determined
by the program from the data. The result is a slightly higher fitting
error (in this case 4.5% rather than 4.4%), but - perhaps
surprisingly - the peak parameter measurements are usually more accurate and more reproducible (Specifically,
the relative standard deviations are on average lower for the
equal-width fit than for an unconstrained-width fit to the
same data, assuming of course that the true underlying peak
widths are really equal). This is an exception to the
general expectation that lower fitting errors result in lower
peak parameter errors. It is an illustration of the general
rule that the more you know about the nature of your signals,
and the closer your chosen model adheres to that knowledge,
the better the results. In this case we knew that the peak
shape was Gaussian (although we could have verified that
choice by trying other candidate peaks shapes). We
determined that the number of peaks was 2 by inspecting the
residuals and fitting errors for 1, 2, and 3 peak
models. And then we introduced the constraint of equal
peak widths within each group of peaks, based on prior
knowledge of the experiment rather than on inspection of
residuals and fitting errors. Here's another example, with
real experimental data from a measurement where the peak
widths are expected to be equal, showing the result
of an unconstrained fit and
an equal width fit; the
fitting errors is slightly larger for the equal-width fit, but
that is to be preferred in this case. Not every experiment
can be expected to yield peaks of equal width, but when it
does, it's better to make use of that constraint.
Fixed-width shapes. Going
one step beyond equal
widths (in peakfit version 7.6 and later), you can
also specify a fixed-width
shapes (shape numbers 11, 12, 34-37), in which the width
of the peaks are known beforehand, but are not
necessarily equal, and are specified as a vector in
input argument 10, one element for each peak, rather than
being determined from the data as in the equal-width fit
above. Introducing this constraint onto the previous example,
and supplying an accurate width as the 10th
input argument:
>> [FitResults,MeanFitError]=peakfit([x'
y'],0,0,2,11,0,0,0,0,[1.666 1.666])
FitResults =
Peak#
Position
Height
Width Area
1
3.9943
0.49537
1.666
0.8785
2
5.9924
0.98612
1.666
1.7488
MeanFitError = 4.8128
Comparing to the previous
equal-width fit, the fitting error of 4.8% is larger here
(because there are fewer degrees of freedom to minimize the
error), but the parameter errors, particularly the peaks
heights, are more accurate because the width
information provided in the input argument was more accurate
(1.666) than the width determined by the equal-width fit
(1.5666). Again, not every experiment yields peaks of known
width, but when it does, it's better to make use of that
constraint. For example, see Example 35 and
the Matlab/Octave script WidthTest.m
(typical results for a Gaussian/Lorentzian blend shape shown
below, showing that the more constraints, the greater the
fitting error but the lower the parameter errors, if the
constraints are accurate).
Relative percent error
|
Fitting error
|
Position Error
|
Height Error
|
Width Error
|
Unconstrained shape factor
and widths: shape 33
|
0.78
|
0.39
|
0.80
|
1.66
|
Fixed shape factor and
variable widths: shape 13
|
0.79
|
0.25
|
1.3
|
0.98
|
Fixed shape factor and
fixed widths: shape 35
|
0.8
|
0.19
|
0.69
|
0.0
|
Multiple
linear regression (peakfit version 9). Finally, note
that if the peak positions
are also known, and only the peak heights are unknown, you don't even need to
use the iterative fitting method at all; you can use the
easier and faster multilinear regression technique
(also called "classical
least squares") which is implemented by the function cls.m and by version 9 of peakfit.m as shape
number 50. Although multilinear regression results in fitting
error slightly greater (and R2 lower), the errors in
the measured peak heights are often less, as in this
example from peakfit9demo.m,
where the true peak heights of the three
overlapping Gaussian peaks are 10, 30, and 20.
Multilinear regression results (known position and
width):
Peak Position
Height Width
Area
1
400
9.9073
70 738.22
2
500
29.995
85 2714
3
560
19.932
90 1909.5
%fitting error=1.3048 R2= 0.99832
%MeanHeightError=0.427
Unconstrained iterative
non-linear least squares results:
Peak Position
Height Width
Area
1
399.7
9.7737
70.234 730.7
2
503.12
32.262
88.217 3029.6
3
565.08
17.381
86.58 1601.9
%fitting error=1.3008 R2= 0.99833
%MeanHeightError=7.63
This demonstrates dramatically how different measurement
methods can look the same, and give fitting errors
almost the same, and yet differ greatly in parameter
measurement accuracy. (The similar script peakfit9demoL.m is the same thing
with Lorentzian peaks).
SmallPeak.m
is a demonstration script comparing all these techniques
applied to the challenging problem of measuring the height of
a small peak that is closely overlapped with and completely
obscured by a much larger peak. It compares unconstrained,
equal-width, and fixed-position iterative fits (using
peakfit.m) with a classical least squares fit in which only
the peak heights are unknown (using cls.m).
It helps to spread out the four figure windows so you can
observe the dramatic difference in stability of the different
methods. A final table of relative percent peak height errors
shows that the more the constraints, the better the
results (but only if the constraints are justified).
The real key is to know which parameters can be relied upon to
be constant and which have to be allowed to vary.
Here's a a
screen video (MorePeaksLowerFittingError.mp4)
of a real-data experiment using the interactive peak fitter ipf.m with a complex experimental signal in
which several different fits were performed using models from
4 to 9 variable-width, equal-width, and fixed-width Gaussian
peaks. The fitting error gradually decreases from 11%
initially to 1.4% as more peaks are used, but is
that really justified? If the objective is simply to get
a good fit, then do whatever it takes. But if the objective is
to extract some useful information from the model peak
parameters, then more specific knowledge about that particular
experiment is needed: how many peaks are really expected; are
the peak widths really expected to be constrained? Note that
in this particular case the residuals (bottom panel) are never
really random and always have a distinct "wavy"
character, suggesting that the data may have been smoothed
before curve fitting (usually not a good idea: see http://wmbriggs.com/blog/?p=195).
Thus there is a real possibility that some of those 9 peaks
are simply "fitting the noise", as will be discussed further
in Appendix A.
b. Background
correction.
The peaks that are measured in many scientific instruments are
sometimes superimposed on a non-specific background or
baseline. Ordinarily the experiment protocol is designed to
minimize the background or to compensate for the background,
for example by subtracting a "blank"
signal from the signal of an actual specimen. But even so
there is often a residual background that can not be
eliminated completely experimentally. The origin and shape of
that background depends on the specific measurement method,
but often this background is a broad, tilted, or curved shape,
and the peaks of interest are comparatively narrow features
superimposed on that background. In some cases the baseline
may be another peak. The presence of the background has
relatively little effect on the peak positions, but it
is impossible to measure the peak heights, width, and areas
accurately unless something is done to account for the
background.
There are various methods
described in the literature for estimating and subtracting the
background in such cases. The simplest assumption is that the
background can be approximated as a simple function in the
local region of group of peaks being fit together, for example
as a constant (flat), straight line (linear) or curved line
(quadratic). This is the basis of the "autozero" modes in the
ipf.m, iSignal.m, and
iPeak.m functions,
which are selected by the T key to cycle thorough OFF,
linear, quadratic, and flat modes. In
the flat mode, a constant baseline is included in the
curve fitting calculation, as described above.
In linear mode, a straight-line baseline connecting
the two ends of the signal segment in the upper panel will be
automatically subtracted before the iterative curve
fitting. In quadratic mode, a parabolic baseline
is subtracted. In the last two modes, you must adjust the pan
and zoom controls to isolate the group of overlapping peaks to
be fit, so that the signal returns to the local background at
the left and right ends of the window.
Example of an
experimental chromatographic signal. From left to right, (1)
Raw data with peaks superimposed on a tilted baseline. One
group of peaks is selected using the the pan and zoom
controls, adjusted so that the signal returns to the local
background at the edges of the segment displayed in the upper
window; (2) The linear baseline is subtracted when the
autozero mode set to 1 in ipf.m by pressing the T key;
(3) Fit with a three-peak Gaussian model, activated by
pressing 3, G, F (3 peaks, Gaussian, Fit).
Alternatively, it may
be better to subtract the background from the entire signal
first, before further operations are performed. As
before, the simplest assumption is that the background is
piece-wise linear, that is, can be approximated as a series of
small straight line segments. This is the basis of the
multiple point background subtraction mode in ipf.m, iPeak.m,
and in iSignal. The user enters
the number of points that is thought to be sufficient to
define the baseline, then clicks where the baseline is thought
to be along the entire length of the signal in the lower
whole-signal display (e.g. on the valleys between the
peaks). After the last point is clicked, the program
interpolates between the clicked points and subtracts the
piece-wise linear background from the original signal.
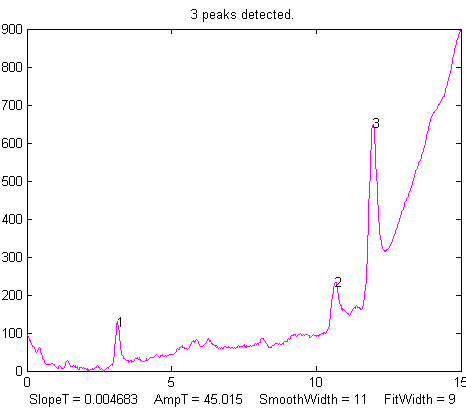
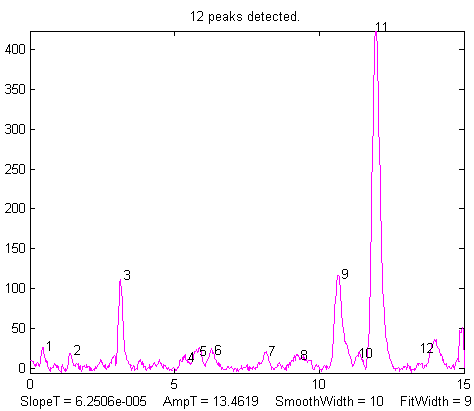
From left to right, (1) Raw
data with peaks superimposed on baseline. (2) Background
subtracted from the entire signal using the multipoint
background subtraction function in iPeak.m (ipf.m and iSignal have the
same function).
Sometimes, even without an actual
baseline present, the peaks may overlap enough so that the
signal never return to the baseline, making it seem that there
is a baseline to be corrected. This can occur especially with
peaks shapes that have gradually sloping sides, such as the
Lorentzian, as shown in
this example. Curve fitting without baseline
correction will work in that case.
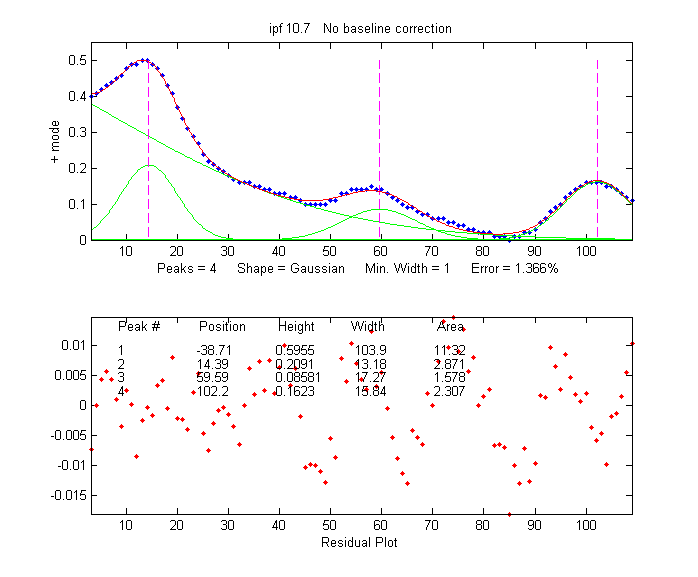 In many cases the background may be
modeled as a broad peak whose maximum falls outside of
the range of data acquired, as in the real-data example on the
left. It may be possible to fit the off-screen peak simply by
including an extra peak in the model to account for the
baseline. In the example on the left, there are three
clear peaks visible, superimposed on a tilted baseline.
In this case the signal was fit nicely with four, rather
than three, variable-width Gaussians, with an error of only
1.3%. The additional broad Gaussian, with a peak at x =
-38.7, serves as the baseline. (Obviously, you shouldn't use
the equal-width shapes for this, because the background peak
is broader than the other peaks).
In many cases the background may be
modeled as a broad peak whose maximum falls outside of
the range of data acquired, as in the real-data example on the
left. It may be possible to fit the off-screen peak simply by
including an extra peak in the model to account for the
baseline. In the example on the left, there are three
clear peaks visible, superimposed on a tilted baseline.
In this case the signal was fit nicely with four, rather
than three, variable-width Gaussians, with an error of only
1.3%. The additional broad Gaussian, with a peak at x =
-38.7, serves as the baseline. (Obviously, you shouldn't use
the equal-width shapes for this, because the background peak
is broader than the other peaks).
In another real-data example of an
experimental
spectrum, the linear baseline subtraction ("autozero")
mode described above is used in conjunction with a 5-Gaussian
model, with one Gaussian component fitting the broad peak that
may be part of the background and the other four fitting the
sharper peaks. This fits the data very well (0.5% fitting
error), but a fit like this can be difficult to get, because
there are so many other solutions with slightly higher fitting
errors; it may take several trials. It
can help if you specify the start values for
the iterated variables, rather than using the default
choices; all the software programs described here have
that capability.
The Matlab/Octave function peakfit.m
can employ a peakshape input argument that is a vector of
different shapes, which can be useful for baseline
correction. As an example, consider a weak Gaussian peak on
sloped straight-line baseline, using a 2-component fit with
one Gaussian component and one variable-slope straight line
('slope', shape 26), specified by using the vector [1 26] as
the shape argument:
x=8:.05:12;y=x+exp(-(x-10).^2);
[FitResults,GOF]= peakfit([x;y],0,0,2,[1 26],[1
1],1,0)
FitResults
=
1
10
1 1.6651
1.7642
2 4.485
0.22297
0.05 40.045
GOF =
0.0928 0.9999
If the baseline seems to be curved rather than straight, you
can model the baseline with a quadratic (shape 46)
rather than a linear slope (peakfit version 8 and
later).
If the baseline seems to be different on either side of the
peak, you can try to model the baseline with an S-shape
(sigmoid), either an up-sigmoid, shape 10 (click for graphic), peakfit([x;y],0,0,2,[1
10],[0 0], or a down-sigmoid, shape 23 (click for graphic), peakfit([x;y],0,0,2,[1
23],[0 0], in these examples leaving the peak modeled
as a Gaussian.
If the signal is very weak compared to the baseline, the fit
can be helped by adding rough first guesses ('start') using
the 'polyfit' function to generate automatic first guesses for
the sloping baseline. For example, with two overlapping
signal peaks and a 3-peak fit with peakshape=[1 1 26].
x=4:.05:16;
y=x+exp(-(x-9).^2)+exp(-(x-11).^2)+.02.*randn(size(x));
start=[8 1 10 1 polyfit(x,y,1)];
peakfit([x;y],0,0,3,[1 1 26],[1 1 1],1,start)
A similar technique can be employed in
a spreadsheet, as
demonstrated in CurveFitter2GaussianBaseline.xlsx
(graphic).
The downside to
including the baseline as
a variable component is that it increases the number
of degrees of freedom, increases the execution time,
and increases the possibility of unstable fits.
Specifying start values can help.
c. Random
noise in the signal. 
Any experimental signal has a certain amount of random noise,
which means that the individual data points scatter randomly
above and below their mean values. The assumption is
ordinarily made that the scatter is equally above and below
the true signal, so that the long-term average approaches the
true mean value; the noise "averages to zero" as it is often
said. The practical problem is that any given recording of the
signal contains only one finite sample of the noise. If
another recording of the signal is made, it will contain
another independent sample of the noise. These noise samples
are not infinitely long and therefore do not represent the
true long-term nature of the noise. This presents two
problems: (1) an individual sample of the noise will not
"average to zero" and thus the parameters of the
best-fit model will not necessarily equal the true values, and
(2) the magnitude of the noise during one sample might not be
typical; the noise might have been randomly greater or smaller
than average during that time. This means that the
mathematical "propagation of error" methods, which seek to
estimate the likely error in the model parameters based on the
noise in the signal, will be subject to error (underestimating the error
if the noise happens to be lower
than average and overestimating
the errors if the noise happens to be larger than average).
A better way to
estimate the parameter errors is to record multiple samples of
the signal, fit each of those separately, compute the models
parameters from each fit, and calculate the standard error of
each parameter. But if that is not practical, it is possible
to simulate such measurements by adding random noise to a
model with known parameters, then fitting that simulated noisy
signal to determine the parameters, then repeating the
procedure over and over again with different sets of random
noise. This is exactly what the script DemoPeakfit.m (which requires the peakfit.m function) does for simulated
noisy peak signals such as those illustrated below. It's easy
to demonstrate that, as expected, the average fitting error
precision and the relative standard deviation of the
parameters increases directly with the random noise level in
the signal. But the precision and the accuracy of the measured
parameters also
depend on which parameter it is (peak positions are always
measured more accurately than their heights, widths, and
areas) and on the peak height and extent of peak overlap (the
two left-most peaks in this example are not only weaker but
also more overlapped than the right-most peak, and therefore
exhibit poorer parameter measurements). In this example, the
fitting error is 1.6% and the percent relative standard
deviation of the parameters ranges from 0.05% for the peak
position of the largest peak to 12% for the peak area of the
smallest peak.
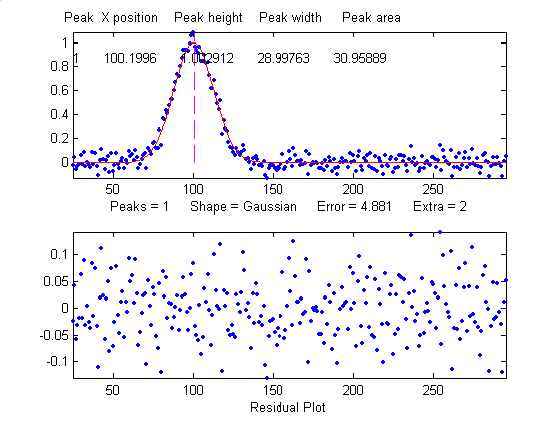
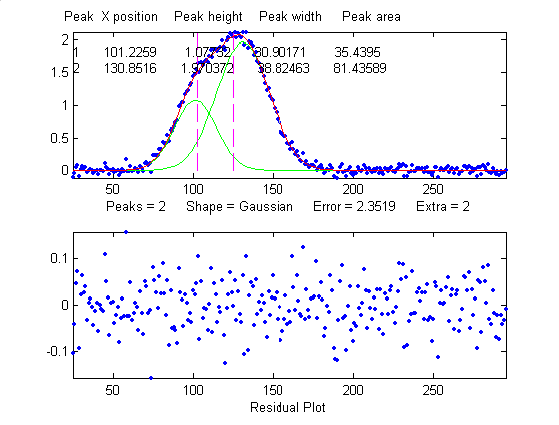
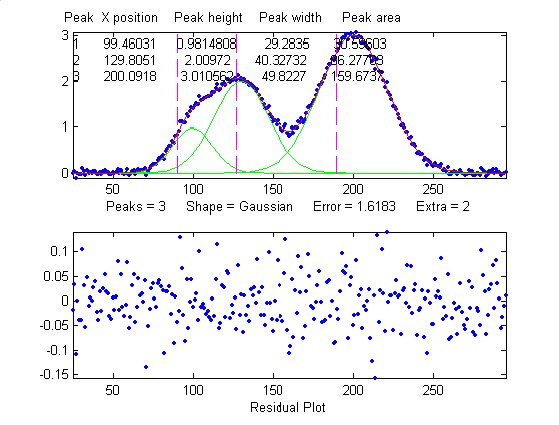
Overlap
matters: The errors in the values of peak parameters
measured by curve fitting depend not only on the
characteristics of the peaks in question and the
signal-to-noise ratio, but also upon other peaks that are
overlapping it. From left to right: (1) a single peak at
x=100 with a peak height of 1.0 and width of 30 is fit with a
Gaussian model, yielding a relative fit error of 4.9% and
relative standard deviation of peak position, height, and
width of 0.2%, 0.95%, and 1.5% , respectively. (2) The
same peak, with the same noise level but with another peak
overlapping it, reduces the relative fit error to
2.4% (because the addition of the second peak increases
overall signal amplitude), but increases the relative
standard deviation of peak position, height, and width to
0.84%, 5%, and 4% - a seemingly better fit, but with
poorer precision for the first peak. (3) The addition
of a third (non-overlapping) peak reduces the fit error to
1.6% , but the relative standard deviation of peak position,
height, and width of the first peak are still 0.8%, 5.8%, and
3.64%, about the same as with two peaks, because the third
peak does not overlap the first one significantly.
 If the average noise noise in
the signal is not known or its probability distribution is
uncertain, it is possible to use the bootstrap sampling method
to estimate the uncertainty of the peak heights, positions,
and widths, as illustated on the left and as described in
detail above. The latest version
of the keypress
operated interactive version of ipf.m has added a function (activated by the
'v' key) that estimates the expected standard deviation of the
peak parameters using this method.
If the average noise noise in
the signal is not known or its probability distribution is
uncertain, it is possible to use the bootstrap sampling method
to estimate the uncertainty of the peak heights, positions,
and widths, as illustated on the left and as described in
detail above. The latest version
of the keypress
operated interactive version of ipf.m has added a function (activated by the
'v' key) that estimates the expected standard deviation of the
peak parameters using this method.
One way to reduce the effect of
noise is to take more data. If the experiment makes it
possible to reduce the x-axis interval between points, or to
take multiple readings at each x-axis values, then the
resulting increase in the number of data points in each peak
should help reduce the effect of noise. As a
demonstration, using the script DemoPeakfit.m
to create a simulated overlapping peak signal like that shown
above right, it's possible to change the interval between x
values and thus the total number of data points in the signal.
With a noise level of 1% and 75 points in the signal, the
fitting error is 0.35 and the average parameter error is 0.8%.
With 300 points in the signal and the same noise level, the
fitting error is essentially the same, but the average
parameter error drops to 0.4%, suggesting that the accuracy of
the measured parameters varies inversely with the square root
of the number of data points in the peaks.
 The figure
on the right illustrates the importance of sampling interval
and data density. You can download the data file "udx" in TXT format or in Matlab MAT format. The signal consists of two
Gaussian peaks, one located at x=50 and the second at x=150.
Both peaks have a peak height of 1.0 and a peak half-width of
10, and normally-distributed random white noise with a
standard deviation of 0.1 has been added to the entire signal.
The x-axis sampling interval, however, is different for the
two peaks; it's 0.1 for the first peak and 1.0 for the second
peak. This means that the first peak is characterized by ten
times more points than the second peak. When you fit these
peaks separately to a Gaussian model (e.g., using peakfit.m or
ipf.m), you will find that all the parameters of the first
peak are measured more accurately than the second, even though
the fitting error is not much different:
The figure
on the right illustrates the importance of sampling interval
and data density. You can download the data file "udx" in TXT format or in Matlab MAT format. The signal consists of two
Gaussian peaks, one located at x=50 and the second at x=150.
Both peaks have a peak height of 1.0 and a peak half-width of
10, and normally-distributed random white noise with a
standard deviation of 0.1 has been added to the entire signal.
The x-axis sampling interval, however, is different for the
two peaks; it's 0.1 for the first peak and 1.0 for the second
peak. This means that the first peak is characterized by ten
times more points than the second peak. When you fit these
peaks separately to a Gaussian model (e.g., using peakfit.m or
ipf.m), you will find that all the parameters of the first
peak are measured more accurately than the second, even though
the fitting error is not much different:
First
peak:
Second peak:
Percent Fitting
Error=7.6434% Percent Fitting Error=8.8827%
Peak# Position Height
Width Peak# Position Height Width
1
49.95 1.0049 10.111 1
149.64 1.0313 9.941
So far this discussion has applied
to white noise. But other noise colors have
different effects. Low-frequency weighted ("pink") noise has a
greater effect on the accuracy of peak parameters
measured by curve fitting, and, in a nice symmetry,
high-frequency "blue" noise has a smaller effect on
the accuracy of peak parameters that would be expected on the
basis of its standard deviation, because the information in a
smooth peak signal
is concentrated at low frequencies. An example of this
occurs when curve fitting is applied to a signal that has been
deconvoluted to remove a
broadening effect. This is why smoothing
before curve fitting does not help, because the peak
signal information is concentrated in the low frequency
range, but smoothing reduces mainly the noise in the high
frequency range.
Sometime you may
notice that the residuals in a curve fitting
operation are structured into bands or lines
rather than being completely random. This can
occur if either the independent
variable or the dependent
variable is quantized into discrete steps rather than
continuous. It may look strange, but it has little
effect on the results as long as the random noise
is larger than the steps.
When there is noise in
the data (in other words, pretty much always), the
exact results will depend on the region selected
for the fit - for example, the results will vary
slightly with the pan and zoom setting in ipf.m,
and the more noise, the greater the effect.
d. Iterative fitting
errors. 
Unlike multiple linear regression curve fitting, iterative
methods may not always converge on the exact same model
parameters each time the fit is repeated with slightly
different starting values (first guesses). The Interactive Peak Fitter
ipf.m makes it easy to test this, because it uses 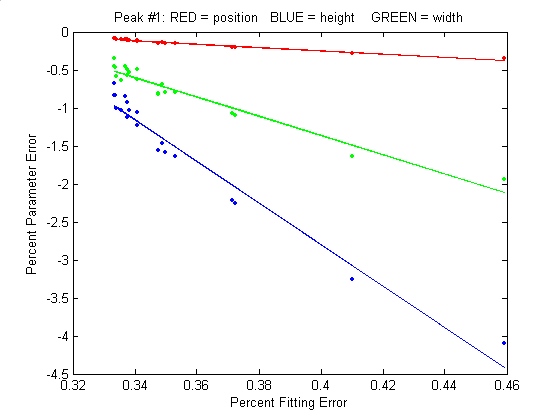 slightly
different starting values each time the signal is fit (by
pressing the F key in
ipf.m,
for example). Even better, by pressing the X key, the ipf.m function
silently computes 10 fits with different starting values and
takes the one with the lowest fitting error. A basic
assumption of any curve fitting operation is that the fitting
error (the root-mean-square difference between the model and
the data) is minimized, the parameter errors (the difference
between the actual parameters and the parameters of the
best-fit model) will also be minimized. This is generally a
good assumption, as demonstrated by the graph to the
right, which shows typical percent parameters errors as a
function of fitting error for the left-most peak in one sample
of the simulated signal generated by DemoPeakfit.m (shown in the
previous section). The variability of the fitting error here
is caused by random small variations in the first guesses,
rather than by random noise in the signal. In many
practical cases there is enough random noise in the signals
that the iterative fitting errors within one sample of the
signal are small compared to the random noise errors between
samples.
slightly
different starting values each time the signal is fit (by
pressing the F key in
ipf.m,
for example). Even better, by pressing the X key, the ipf.m function
silently computes 10 fits with different starting values and
takes the one with the lowest fitting error. A basic
assumption of any curve fitting operation is that the fitting
error (the root-mean-square difference between the model and
the data) is minimized, the parameter errors (the difference
between the actual parameters and the parameters of the
best-fit model) will also be minimized. This is generally a
good assumption, as demonstrated by the graph to the
right, which shows typical percent parameters errors as a
function of fitting error for the left-most peak in one sample
of the simulated signal generated by DemoPeakfit.m (shown in the
previous section). The variability of the fitting error here
is caused by random small variations in the first guesses,
rather than by random noise in the signal. In many
practical cases there is enough random noise in the signals
that the iterative fitting errors within one sample of the
signal are small compared to the random noise errors between
samples.
Remember that the variability in
measured peak parameters from fit to fit of a single sample of
the signal is not a
good estimate of the precision or accuracy of those
parameters, for the simple reason that those results represent
only one sample of the signal, noise, and background. The
sample-to-sample variations are likely to be much greater than
the within-sample variations due to the iterative curve
fitting. (In this case, a "sample" is a single recording of
signal). To estimate the contribution of random noise to the
variability in measured peak parameters when only a single
sample if the signal is available, the bootstrap method can
be used.
e. Selecting
the optimum data region of interest. When
you perform a peak fitting using ipf.m,
you have control over data region selected by using the pan
and zoom controls (or, using the command-line function
peakfit.m, by setting the center and window input arguments).
Changing these settings usually changes the resulting fitted
peak parameters. If the data were absolutely perfect, say, a
mathematically perfect peak shape with no random noise, then
the pan and zoom settings would make no difference at all; you
would get the exact same values for peak parameters at all
settings, assuming only that the model you are using matches
the actual shape. But of course in the real world, data are
never mathematically perfect and noiseless. The greater the
amount of random noise in the data, or the greater the
discrepancy between your data and the model you select, the
more the measured parameters will vary if you fit different
regions using the pan and zoom controls. This is simply an
indication of the uncertainty in the measured parameters.
f. A difficult case. As
a dramatic example of the ideas in parts c and d, consider 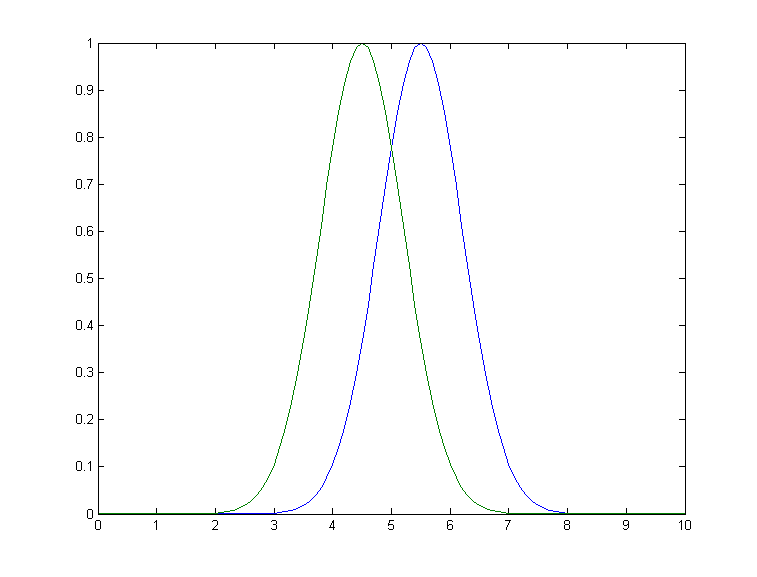 this
simulated example signal, consisting of two Gaussian peaks of
equal height = 1.00, overlapping closely enough so that their
sum is a single symmetrical peak that looks very much like
a single Gaussian.
this
simulated example signal, consisting of two Gaussian peaks of
equal height = 1.00, overlapping closely enough so that their
sum is a single symmetrical peak that looks very much like
a single Gaussian.
>> x=[0:.1:10]';
>>
y=exp(-(x-5.5).^2)+exp(-(x-4.5).^2);
If there were no noise in the
signal, the peakfit.m or ipf.m routines could easily extract
the two equal Gaussian components to an accuracy of 1 part in
1000.
>> peakfit([x y],5,19,2,1)
Peak# Position Height Width
Area
1 4.5004 1.001 1.6648 1.773
2 5.5006
0.99934 1.6641 1.770
But in the presence of even a
little noise (for example, 1% RSD), the results are uneven;
one peak is almost always significantly higher than the other:
>>
y=exp(-(x-5.5).^2)+exp(-(x-4.5).^2)+.01*randn(size(x))
>> peakfit([x
y],5,19,2,1)
Peak#
Position Height
Width Area
1
4.4117
0.83282
1.61 1.43
2
5.4022
1.1486 1.734 2.12
The fit is stable with any one
sample of noise (if peakfit.m
was run again with slightly different starting values, for
example by pressing the F
key several times in ipf.m),
so the problem is not iterative fitting errors caused by
different starting values. The problem is the noise: although
the signal is completely symmetrical, any particular sample of
the noise is not perfectly symmetrical (e.g. the
first half of the noise usually averages a slightly higher or
lower than the second half, resulting in an asymmetrical fit
result). The surprising thing is that the error in the peak
heights are much larger (about 15% relative, on average) than
the random noise in the data (1% in this example). So even
though the fit looks good
- the fitting error is low (less than 1%) and the residuals
are random and unstructured - the model parameters can
still be very far off. If you were to make another
measurement (i.e. generate another independent set of noise),
the results would be different but still inaccurate (the
first peak has an equal chance of being larger or smaller than
the second). Unfortunately, the expected error is not
accurately predicted by the bootstrap method,
which seriously underestimates the standard deviation of the
peak parameters with repeated measurements of independent
signals (because a bootstrap sub-sample of asymmetrical
noise is likely to remain asymmetrical). A Monte Carlo
simulation would give a more reliable estimation of
uncertainty in such cases.
Better results can be obtained in
cases where the peak widths are expected to be equal, in which
case you can use peak shape 6 (equal-width Gaussian) instead
of peak shape 1: peakfit([x
y],5,19,2,6).
It also helps to provide decent first guesses (start) and to
set the number of trials (NumTrials) to a number above 1): peakfit([x,y],5,10,2,6,0,10,[4
2 5 2],0,0). The best case will be if the shape,
position, and width of the two peaks are known accurately, and
if the only unknown is their heights. Then the Classical Least Squares (multiple
regression) technique can be employed and the results
will be much better.
Appendix AE
illustrates one way to deal with the problem of excessive peak
overlap in a multi-step script that uses first-derivative
symmetrization as a pre-process performed before iterative
least-squares curve fitting to analyze a complex signal
consisting of multiple asymmetric overlapping peaks. This
results in better peak parameter accuracy, even though
the fitting error is no better.
For an even more challenging
example like this, where the two closely overlapping peak are
very different in height, see Appendix Q.
So, to sum up, we can make the following observations about the
accuracy of model parameters: (1) the parameter errors depend on
the accuracy of the model chosen and on number of peaks; (2) the
parameter errors are directly proportional to the noise in the
data (and worse for low-frequency or pink noise); (3) all else
being equal, parameter errors are proportional to the fitting
error, but a model that fits the underlying reality better, e.g.
equal or fixed widths or shapes) often gives lower parameter
errors even if the fitting error is larger; (4) the errors are
typically least for peak position and worse for peak width and
area; (5) the errors depend on the
data density (number
of independent data points in the width of each peak) and on the
extent of peak overlap (the parameters of isolated peaks
are easier to measure than highly overlapped peaks); (6) if only
a single signal is available, the effect of noise on the
standard deviation of the peak parameters in many cases can be
predicted approximately by the
bootstrap method, but
if the overlap of the peaks is too great, the error of the
parameter measurements can be much greater than predicted.
Fitting
signals that are subject to exponential broadening.
DataMatrix2
(figure on the right) is a computer-generated test signal
consisting of 16 symmetrical
Gaussian peaks with random whi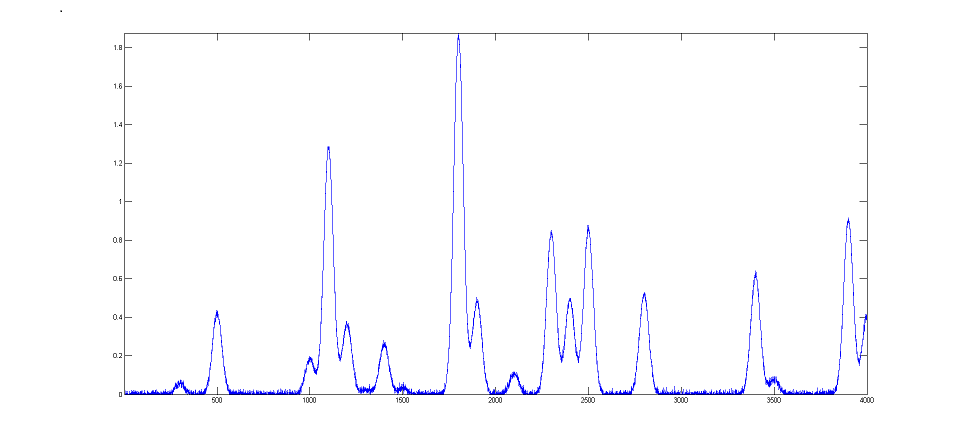 te noise added. The peaks occur
in groups of 1, 2, or 3 overlapping peaks, but the peak
maxima are located at exactly integer values of x from 300
to 3900 (on the 100's) and the peak widths are always
exactly 60 units. The peak heights vary from 0.06 to 1.85.
The standard deviation of the noise is 0.01. You can use
this signal to test curve-fitting programs and to
determine the accuracy of their measurements of peak
parameters. Right-click and select "Save" to download this
signal, put it in the Matlab path, then type "load DataMatrix2"
at the command prompt to load it into the Matlab
workspace.
te noise added. The peaks occur
in groups of 1, 2, or 3 overlapping peaks, but the peak
maxima are located at exactly integer values of x from 300
to 3900 (on the 100's) and the peak widths are always
exactly 60 units. The peak heights vary from 0.06 to 1.85.
The standard deviation of the noise is 0.01. You can use
this signal to test curve-fitting programs and to
determine the accuracy of their measurements of peak
parameters. Right-click and select "Save" to download this
signal, put it in the Matlab path, then type "load DataMatrix2"
at the command prompt to load it into the Matlab
workspace.
DataMatrix3
(figure on the left) i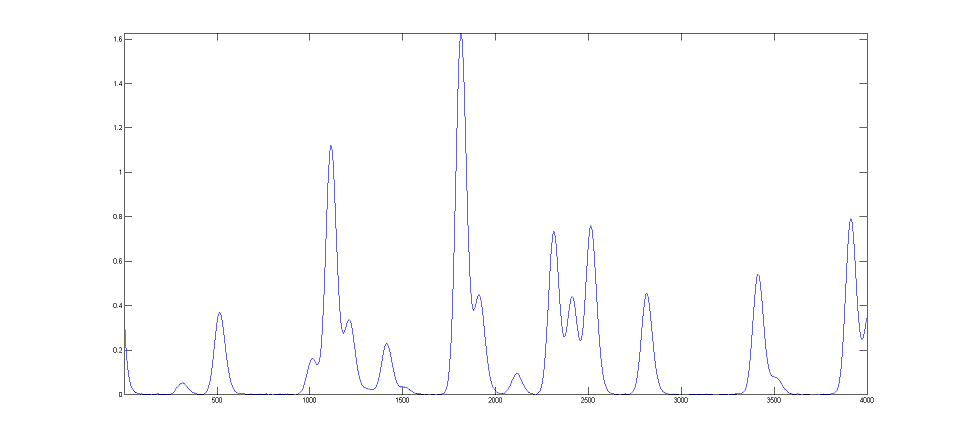 s a exponentially
broadened version of DataMatrix2, with a "decay
constant", also called "time constant", of 33 points on
the x-axis. The result of the exponential broadening
is that all the peaks in this signal are
asymmetrical, their peak maxima are shifted to longer x
values, and their peak heights are smaller and their peak widths are larger than the corresponding peaks in
DataMatrix2. Also, the random noise is damped in this
signal compared to the
original and is no longer "white",
as a consequence of the broadening. This type of effect is common
in physical measurements and often arises from some
physical or electrical effect in the measurement system
that is apart from the fundamental peak characteristics.
In such cases it is usually desirable to compensate for
the effect of the broadening, either by deconvolution
or by curve fitting, in an attempt to measure what the
peak parameters would have been before the broadening (and also to
measure the broadening itself). This can be done for
Gaussian peaks that are exponentially broadened by using
the "ExpGaussian" peak shape in peakfit.m and ipf.m (or
the "ExpLorentzian", if the underlying peaks are
Lorentzian). Right-click and select "Save" to
download this signal, put it in the Matlab path, then type
"load DataMatrix3"
to load it into the Matlab workspace.
s a exponentially
broadened version of DataMatrix2, with a "decay
constant", also called "time constant", of 33 points on
the x-axis. The result of the exponential broadening
is that all the peaks in this signal are
asymmetrical, their peak maxima are shifted to longer x
values, and their peak heights are smaller and their peak widths are larger than the corresponding peaks in
DataMatrix2. Also, the random noise is damped in this
signal compared to the
original and is no longer "white",
as a consequence of the broadening. This type of effect is common
in physical measurements and often arises from some
physical or electrical effect in the measurement system
that is apart from the fundamental peak characteristics.
In such cases it is usually desirable to compensate for
the effect of the broadening, either by deconvolution
or by curve fitting, in an attempt to measure what the
peak parameters would have been before the broadening (and also to
measure the broadening itself). This can be done for
Gaussian peaks that are exponentially broadened by using
the "ExpGaussian" peak shape in peakfit.m and ipf.m (or
the "ExpLorentzian", if the underlying peaks are
Lorentzian). Right-click and select "Save" to
download this signal, put it in the Matlab path, then type
"load DataMatrix3"
to load it into the Matlab workspace. 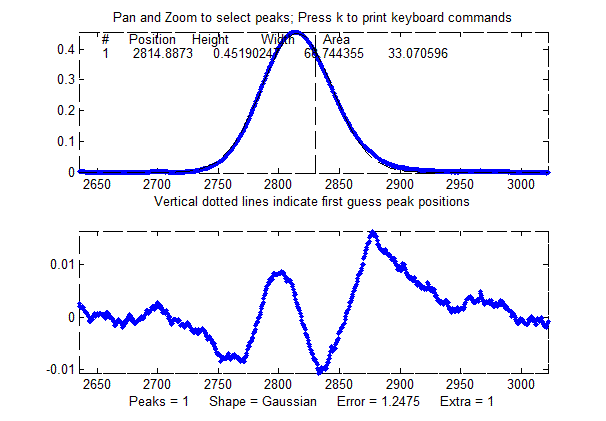
The example illustrated on the
right focuses on the single isolated peak whose "true" peak position, height,
width, and area in the original unbroadened signal, are 2800, 0.52, 60, and 33.2 respectively. (The relative standard
deviation of the noise is 0.01/0.52=2%.) In the broadened
signal, the peak is visibly asymmetrical, the peak maximum
is shifted to larger x values, and it has a shorter height
and larger width, as demonstrated by the attempt to fit a
normal (symmetrical) Gaussian to the broadened peak. (The
peak area, on
the other hand, is not much effected by the
broadening).
>> load DataMatrix3
>>
ipf(DataMatrix3);
Peak
Shape = Gaussian
Autozero
ON
Number of
peaks = 1
Fitted
range = 2640 - 2979.5 (339.5) (2809.75)
Percent
Error = 1.2084
Peak# Position Height
Width Area
1
2814.832 0.45100549 68.441262 32.859436
The
large "wavy" residual in the plot above is a tip-off that the
model is not quite right. Moreover, the fitting error (1.2%)
is larger than expected for a peak with a half-width of 60
points and a 2% noise RSD (approximately 2%/sqrt(60)=0.25%).

Fitting to an
exponentially-broadened Gaussian (pictured on the right)
gives a much lower fitting error ("Percent error") and a
more nearly random residual plot. But the interesting
thing is that it also recovers the original peak
position, height, and width to an accuracy of a fraction
of 1%. In performing this fit, the decay constant
("extra") was experimentally determined from the broadened
signal by adjusting it with the A and Z keys to give the
lowest fitting error; that also results in a reasonably good measurement of the
broadening factor (32.6, vs the actual value of 33). Of
course, had the original signal been nosier, these
measurements would not be so accurate. Note: When using
peakshape 5 (fixed decay constant exponentially broadened
Gaussian) you have to give it a reasonably good value for
the decay constant ('extra'), the input argument
right after the peakshape number. If the value is
too far off, the fit may fail completely, returning all
zeros. A little trial and error suffice. (Also, peakfit.m version 8.4 has two forms
of unconstrained variable decay constant exponentially-broadened
Gaussian, shape numbers 31 and 39, that will measure
the decay constant as an iterated variable. Shape 31 (expgaussian.m) creates
the shape by performing a Fourier convolution of a
specified Gaussian by an exponential decay of
specified decay constant, whereas shape 39 (expgaussian2.m)
uses a
mathematical expression for the final shape so
produced. Both result in the same peak shape but are
parameterized differently. Shape 31 reports the peak
height and position as that of the original Gaussian before
broadening, whereas shape 39 reports the peak height
of the broadened result. Shape 31 reports the
width as the FWHM (full width at half maximum) and
shape 39 reports the standard deviation (sigma) of
the Gaussian. Shape 31 reports the exponential
factor an the number of data
points and
shape 39 reports the reciprocal of decay
constant in time
units. (See the script DemoExpgaussian.m
for a more detailed numerical example). For multiple-peak
fits, both shapes usually require a reasonable first guess
('start") vector for best results. If the exponential decay
constant of each peak is expected to be different and you
need to measure those values, use shapes 31 or 39, but the decay constant of all the
peaks is expected to be the same, use shape 5, and
determine the decay constant by fitting an isolated peak.
For example:
Peak Shape =
Exponentially-broadened Gaussian
Autozero ON
Number of peaks = 1
Extra = 32.6327
Fitted range = 2640
- 2979.5 (339.5) (2809.75)
Percent Error =
0.21696
Peak# Position
Height
Width Area
1
2800.1302
0.51829906 60.086295 33.152429
Comparing the two methods, the exponentially-broadened Gaussian
fit recovers all the underlying peak parameters quite
accurately:
|
Position
|
Height
|
Width
|
Area
|
Actual peak parameters
|
2800
|
0.52
|
60
|
33.2155
|
Gaussian fit to broadened
signal
|
2814.832
|
0.45100549
|
68.441262
|
32.859436
|
| ExpGaussian fit to broadened
signal |
2800.1302 |
0.51829906
|
60.086295
|
33.152429
|
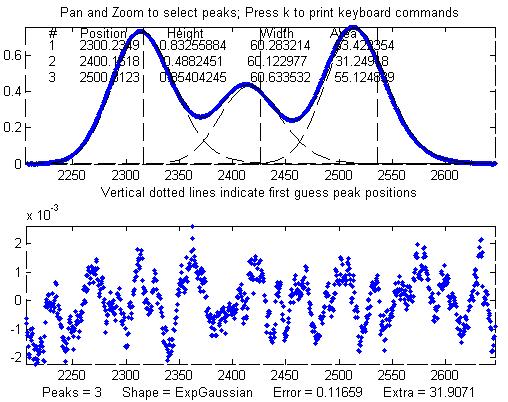 Other peaks in the same signal,
under the broadening influence of the same decay constant,
can be fit with similar settings, for example the set of
three overlapping peaks near x=2400. As before, the
peak positions are recovered almost exactly and even the
width measurements are reasonably accurate (1% or better).
If the exponential
broadening decay constant is not the same for all
the peaks in the signal, for example if it gradually
increases for larger x values, then the decay constant
setting can be optimized for each group of peaks.
Other peaks in the same signal,
under the broadening influence of the same decay constant,
can be fit with similar settings, for example the set of
three overlapping peaks near x=2400. As before, the
peak positions are recovered almost exactly and even the
width measurements are reasonably accurate (1% or better).
If the exponential
broadening decay constant is not the same for all
the peaks in the signal, for example if it gradually
increases for larger x values, then the decay constant
setting can be optimized for each group of peaks.
The smaller fitting error
evident here is just a reflection of the larger peak
heights in this particular group of peaks - the noise is
the same everywhere in this signal.
Peak Shape = Exponentially-broadened
Gaussian
Autozero OFF
Number of peaks = 3
Extra = 31.9071
Fitted range = 2206
- 2646.5 (440.5) (2426.25)
Percent Error =
0.11659
Peak#
Position Height
Width Area
1 2300.2349 0.83255884
60.283214
53.422354
2 2400.1618 0.4882451 60.122977 31.24918
3
2500.3123
0.85404245
60.633532 55.124839
The residual plots in both of
these examples still have some "wavy" character, rather than
being completely
random and "white". The exponential broadening
smooths out any white noise in the original signal that is
introduced before
the exponential effect, acting as a low-pass filter in the
time domain and resulting in a low-frequency dominated
"pink" noise, which is what remains in the residuals after
the broadened peaks have been fit as well as possible. On
the other hand, white noise that is introduced after the exponential effect would
continue to appear white and random on the
residuals. In real experimental data, both types of
noise may be present in varying amounts.

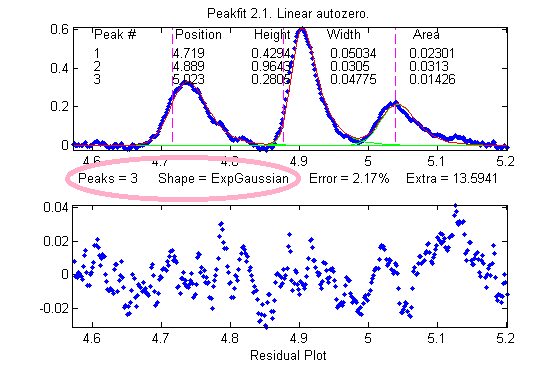 One final caveat: peak asymmetry
similar to exponential broadening could possibly be the
result a pair of closely-spaced peaks of
different peak heights. In fact, a single
exponential broadened Gaussian peak can sometimes be fit
with two symmetrical
Gaussians to a fitting error at least as low as a single exponential broadened Gaussian
fit. This makes it hard to distinguish between these
two models on the basis of fitting error alone. However,
this can usually be decided by inspecting the other peaks
in the signal: in most experiments, exponential broadening
applies to every peak in the signal, and the broadening is
either constant or changes gradually over the length of
the signal. On the other hand, it is relatively unlikely
that every peak in the signal will be accompanied by a
smaller side peak that varies in this way. So, if a only
one or a few of the peaks exhibit asymmetry, and the
others are symmetrical, it's most likely that the asymmetry is due to closely-spaced peaks of
different peak heights. If all peaks have the same or similar asymmetry, it's more likely to
be a broadening factor that applies to the entire signal.
The two figures here provide an example from real
experimental data. On the left, three asymmetrical peaks
are each fit with two symmetrical Gaussians (six peaks
total). On the right, those three peaks are fit with one
exponentially broadened Gaussian each (three peaks total).
In this case, the three asymmetrical peaks all
have the same asymmetry and can be fit with the same decay
constant ("extra"). Moreover, the fitting error is
slightly lower for the three-peak exponentially broadened fit.
Both of these observations argue for the three-peak exponentially broadened fit
rather than the six-peak fit.
One final caveat: peak asymmetry
similar to exponential broadening could possibly be the
result a pair of closely-spaced peaks of
different peak heights. In fact, a single
exponential broadened Gaussian peak can sometimes be fit
with two symmetrical
Gaussians to a fitting error at least as low as a single exponential broadened Gaussian
fit. This makes it hard to distinguish between these
two models on the basis of fitting error alone. However,
this can usually be decided by inspecting the other peaks
in the signal: in most experiments, exponential broadening
applies to every peak in the signal, and the broadening is
either constant or changes gradually over the length of
the signal. On the other hand, it is relatively unlikely
that every peak in the signal will be accompanied by a
smaller side peak that varies in this way. So, if a only
one or a few of the peaks exhibit asymmetry, and the
others are symmetrical, it's most likely that the asymmetry is due to closely-spaced peaks of
different peak heights. If all peaks have the same or similar asymmetry, it's more likely to
be a broadening factor that applies to the entire signal.
The two figures here provide an example from real
experimental data. On the left, three asymmetrical peaks
are each fit with two symmetrical Gaussians (six peaks
total). On the right, those three peaks are fit with one
exponentially broadened Gaussian each (three peaks total).
In this case, the three asymmetrical peaks all
have the same asymmetry and can be fit with the same decay
constant ("extra"). Moreover, the fitting error is
slightly lower for the three-peak exponentially broadened fit.
Both of these observations argue for the three-peak exponentially broadened fit
rather than the six-peak fit.
Note: if your peaks are trailing
off to the left, rather that to the right as in the above
examples, simply use a negative value for the
decay constant (in ipf.n, press Shift-X and type a
negative values).
An alternative to this type of
curve fitting for exponential broadened peaks is to
use the first-derivative
addition technique to remove the asymmetry and then
fit the resulting peak with a symmetrical model. This is
faster in terms of computer execution time, especially for
signals with many peaks, but it requires that the
exponential time constant be known or estimated
experimentally beforehand.
The Effect of Smoothing
before least-squares analysis.
 In
general,
it is not advisable to smooth a signal
before applying least-squares fitting, because doing so
might distort the signal, can make it hard to evaluate the
residuals properly,
and
might bias the results of bootstrap sampling estimations
of precision, causing it to underestimate the
between-signal variations in peak parameters.
SmoothOptimization.m
is a Matlab/Octave
script that compares the effect of smoothing on the measurements of peak height of a Gaussian peak
with a half-width of 166 points, plus white noise
with a
signal-to-noise ratio (SNR) of 10, using three different methods:
In
general,
it is not advisable to smooth a signal
before applying least-squares fitting, because doing so
might distort the signal, can make it hard to evaluate the
residuals properly,
and
might bias the results of bootstrap sampling estimations
of precision, causing it to underestimate the
between-signal variations in peak parameters.
SmoothOptimization.m
is a Matlab/Octave
script that compares the effect of smoothing on the measurements of peak height of a Gaussian peak
with a half-width of 166 points, plus white noise
with a
signal-to-noise ratio (SNR) of 10, using three different methods:
(a) simply taking the single point at the center of the
peak as the peak height;
(b) using the gaussfit method to fit the top
half of the peak (see CurveFitting.html#Transforming),
and
(c) fitting the entire
signal with a Gaussian using the iterative method.
The results of 150 trials with
independent white noise samples are shown on the left: a
typical raw signal is shown in the upper left. The
other three plots show the effect of the SNR of the
measured peak height vs the smooth ratio (the ratio of the
smooth width to the half-width of the peak) for those
three measurement methods. The results show that the
simple single-point measurement is indeed much improved by
smoothing, as is expected; however, the optimum SNR (which
improves by roughly the square root of the peak width of
166 points) is achieved only when the smooth ratio
approaches 1.0, and that much smoothing distorts the peak
shape significantly, reducing the peak height by about
40%. The curve-fitting methods are much less effected by
smoothing and the iterative method hardly at all. So the
bottom line is that you should not smooth prior to curve-fitting,
because it will distort the peak and will not gain any significant
SNR advantage. The only situations where it might be
advantageous so smooth before fitting are when the noise
in the signal is high-frequency weighted (i.e. "blue" noise), where
low-pass filtering will make the peaks easier to see for
the purpose of setting the staring points for an iterative
fit, or if the signal is contaminated with high-amplitude
narrow spike artifacts, in which case a median-based pre-filter
can remove the spikes without much change to the rest of
the signal. And, in another application altogether, if you
want to fit a curve joining the successive peaks of a
modulated wave (called the "envelope"), then you can
smooth the absolute value of the wave before fitting the
envelope.
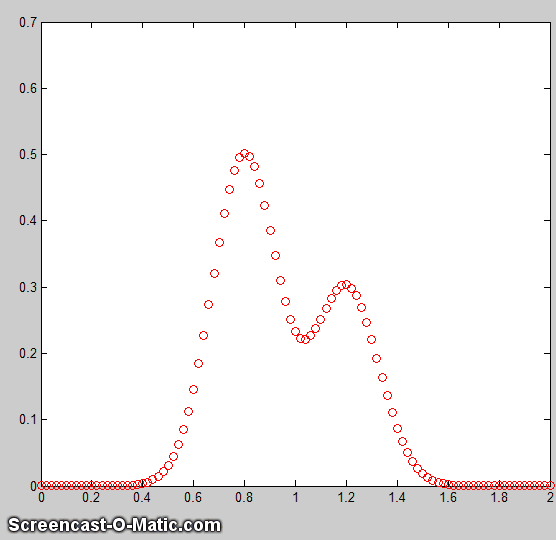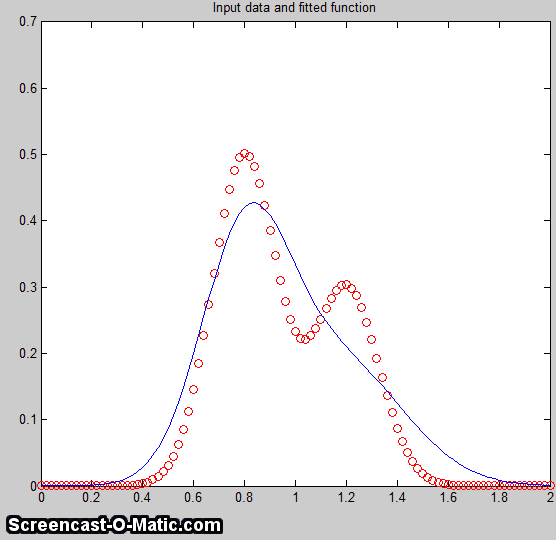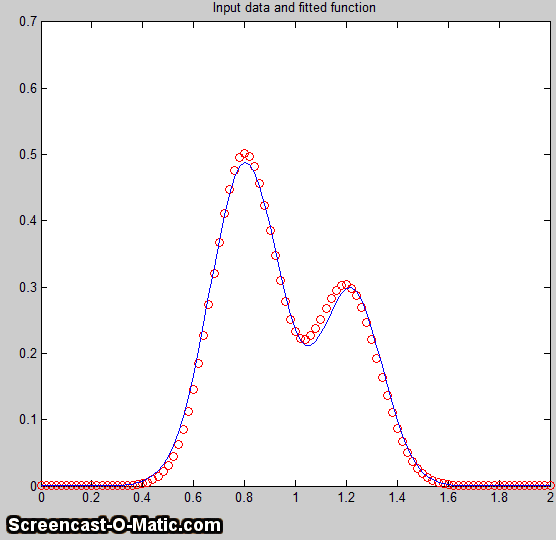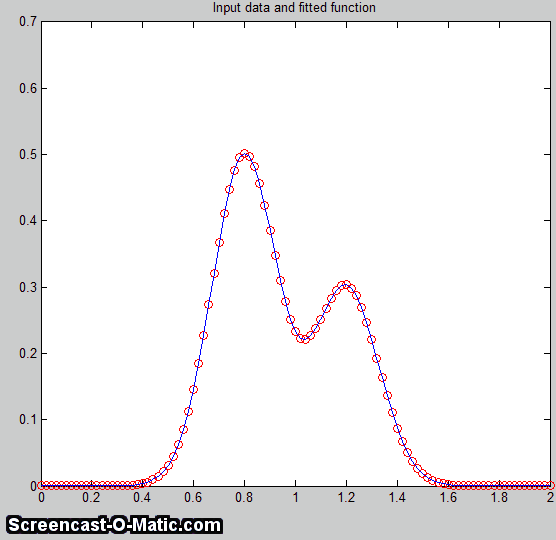 essentially a way of
organizing and optimizing the changes in parameters (step 4,
above) to shorten the
essentially a way of
organizing and optimizing the changes in parameters (step 4,
above) to shorten the 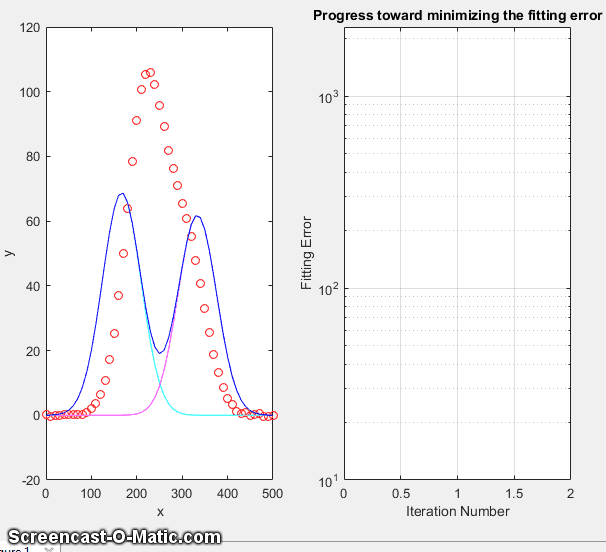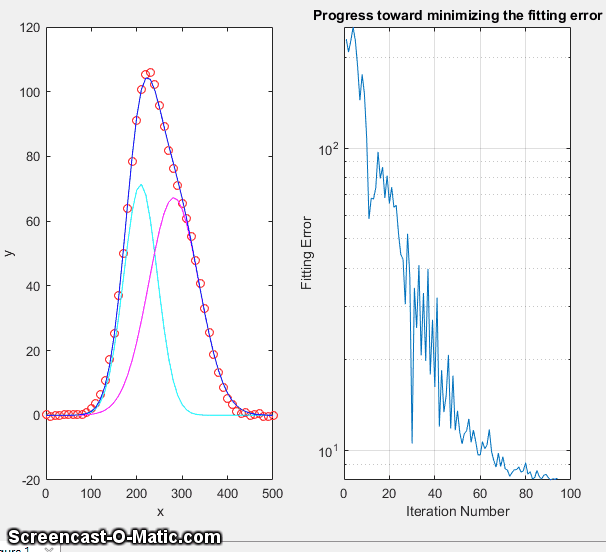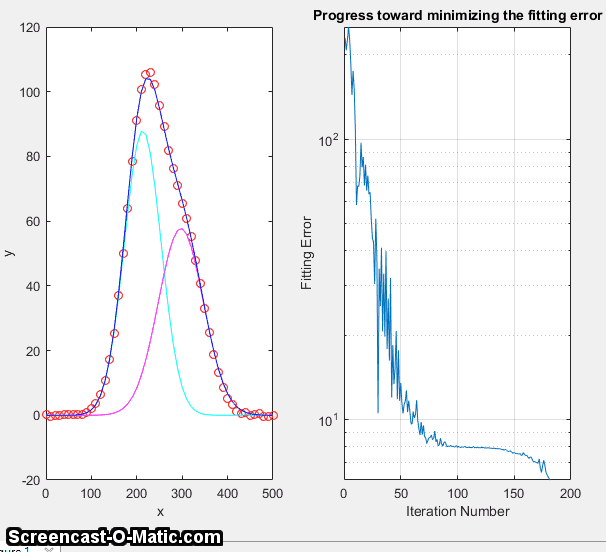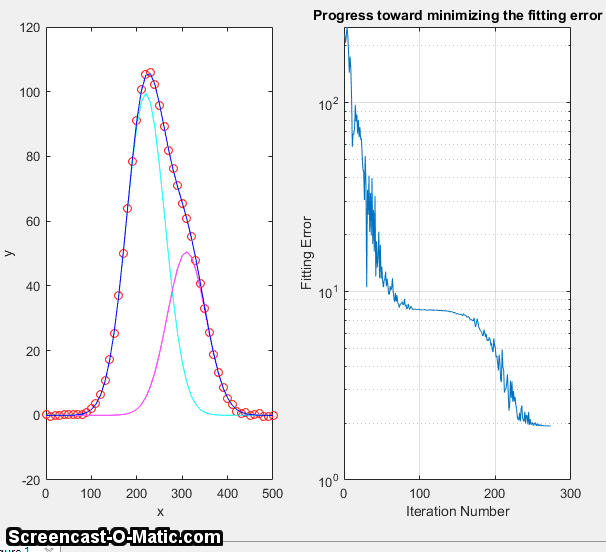 time required to fit the function to the
required degree of accuracy. With contemporary personal computers,
the entire process typically takes only a fraction of a second to
a few seconds, depending on the complexity of the model and the
number of independently adjustable parameters in the model.
time required to fit the function to the
required degree of accuracy. With contemporary personal computers,
the entire process typically takes only a fraction of a second to
a few seconds, depending on the complexity of the model and the
number of independently adjustable parameters in the model.  specified
goal; this can be used in peak fitting to minimize the fitting
error between a set of data and a proposed calculated model,
such as a set of overlapping Gaussian bands.
specified
goal; this can be used in peak fitting to minimize the fitting
error between a set of data and a proposed calculated model,
such as a set of overlapping Gaussian bands.
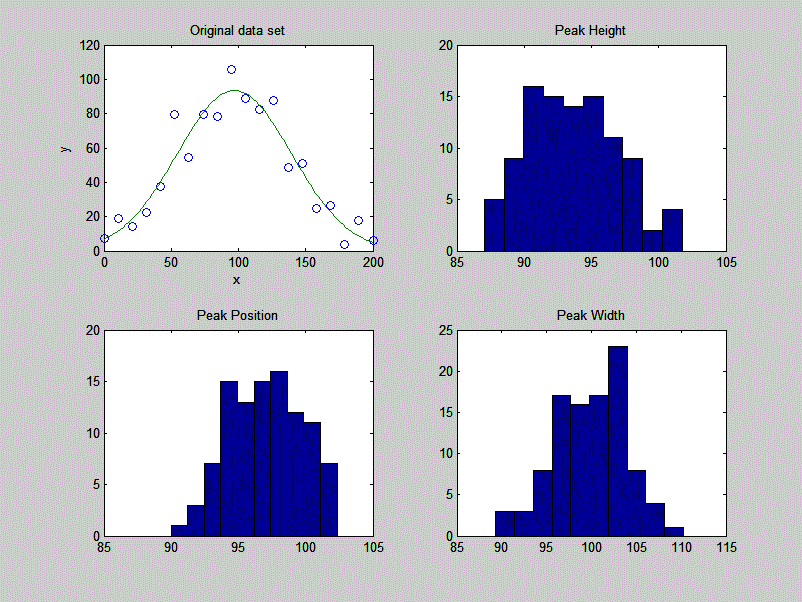
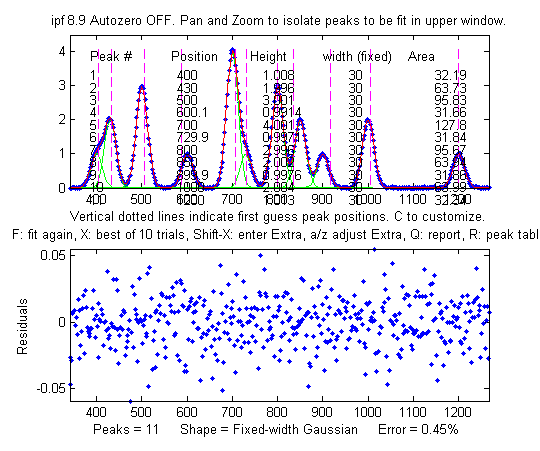 Peak
fitting functions and scripts that uses an unconstrained non-linear optimization algorithm to
decompose a complex, overlapping-peak time-series signal into its
component peaks. The objective is to determine whether your signal
can be represented as the sum of fundamental underlying peaks
shapes. These functions accept signals of any length, including
those with non-integer and non-uniform x-values, and can fit any
number of peaks with
Peak
fitting functions and scripts that uses an unconstrained non-linear optimization algorithm to
decompose a complex, overlapping-peak time-series signal into its
component peaks. The objective is to determine whether your signal
can be represented as the sum of fundamental underlying peaks
shapes. These functions accept signals of any length, including
those with non-integer and non-uniform x-values, and can fit any
number of peaks with 

















