Einstein-Heisenberg Gap: Space-time Entanglement

|
In his article, Heisenberg said he understood the mathematics of Lorentz
transformations, but could not comprehend Einstein's simultaneity or time
separation.
|
|
|

|
|
In 2005, I constructed the webpage entitled
Since then, this webpage has been the most popular page among the many
webpages (nearly 1000) I maintain. In this 2005 page, I review an article
Heisenberg wrote about Einstein. I point out there that Heisenberg had a great
respect for Einstein, but he expresses his frustration over Einstein's refusal to
accept his interpretation of quantum mechanics.
- These days, there is a tendency to exaggerate the difference between
these two great physicists. Many people say that Einstein was totally against
quantum mechanics. This cannot be true. Einstein's photo-electric effect
was one of the first manifestations of the wave-particle duality. Then where was
the gap between Einstein and Heisenberg.
- Heisenberg, while talking about Einstein, said he did not have difficulties in
understanding the mathematics of Lorentz transformations, but he could not
comprehend Einstein's concept of simultaneity.
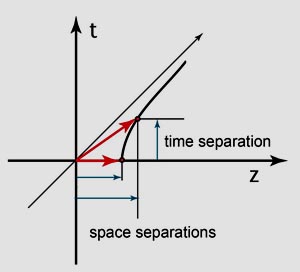
Let us consider the distance between
the proton and electron in the hydrogen atom. This is a space-like separation when
they are observed simultaneously. This is called the Bohr radius, one of the most
important quantities in quantum mechanics. When the atom moves, the space-like
separation picks up a time-like separation.
Was Heisenberg alone having this difficulty? The answer is NO. Einstein and Bohr met
frequently before and
after 1927, to talk about physics,
presumably about relativity and quantum mechanics. However, there is one important
aspect they did not discuss.
Click here for what
they did not discuss. This is the question of simultaneity Heisenberg was talking
about.
Even these days, this time-separation variable is the most difficult item for me
to talk about at conferences. The Physical Review used to reject my papers whenever
I explicitly mentioned this variable, insisting that it does not exist in
quantum mechanics.
Space-time Entanglements
- Let us start with the series
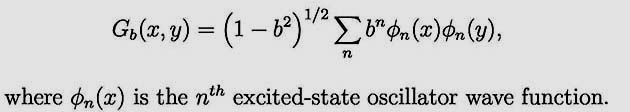
This series appears very frequently in the literature these days.
It is for the Gaussian entanglement of the x and y variables.
Did you know this entanglement series can be written in the
following Gaussian form?
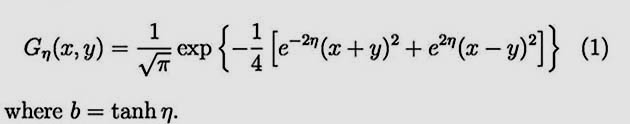
Click here to see how the entanglement series can be
derived from the Gaussian form of Eq.(1).
- If the x and y variables are replaced by the space-time variables
z and t respectively, this Gaussian form becomes

- The entangled Gaussian form of Eq.(2) can now be written as
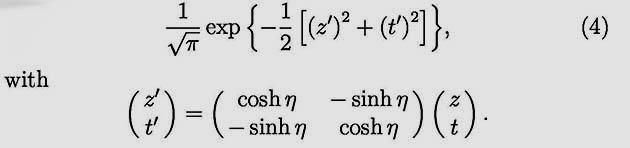
This matrix is clearly the formula for the Lorentz boost along the
z direction. This means that the Lorentz boost entangles the
space and time coordinates. If we Lorentz-boost the Gaussian form
of Eq.(3), it becomes the entangled state of Eq.(2).

|
Both Yukwa and Dirac attempted to construct Lorentz-covariant quantum mechanics
using harmonic oscillators, but they did not have enough experimental data to
rely on.
Click here for a story.
|
The history of Eq.(4) can traced to Yukawa's 1953 paper on
harmonic oscillators for internal space-time structure of elementary
particles. Click here for
a story.
In his paper, Yukawa clearly said z and t are the space and
time separation respectively, but he could not say what the constituent
particles are. The quarks were unknown in 1953.
- The time-separation is in Feynman's rest of the universe, and this
problem can be studied in terms of von Neumann's entropy.
Click here for a detailed story.
You have seen this page before.
- Let us look at another consequence of the space-time entanglement. The
harmonic oscillator is applicable to high-energy hadronic physics. Its
mass spectra are like the degeneracy of the three-dimensional oscillator,
and the ground state oscillator wave function can be used for a
reasonable approximation for the proton. In the three-quark bound sate
for the proton, there are two independent oscillator modes.
We can express the entangled Gaussian form of Eq.(2) for the Lorentz-boosted
proton using squeezed circles, and construct the following figure.
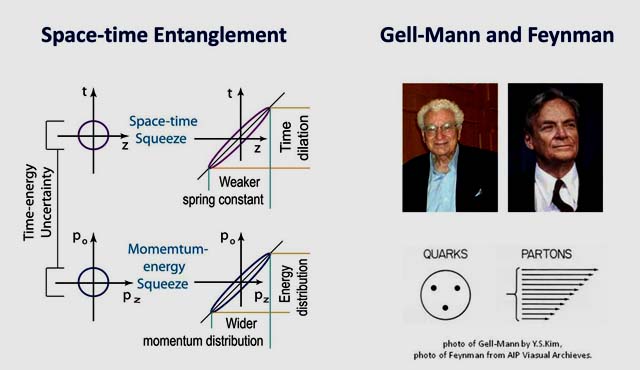 Gell-Mann's quark model and Feynman's parton model tell different stories
of the proton. The entanglement diagram shown above tells the quark model
and parton model are two different manifestations of one Lorentz-covariant
entity. Click here for a more
detailed story.
Gell-Mann's quark model and Feynman's parton model tell different stories
of the proton. The entanglement diagram shown above tells the quark model
and parton model are two different manifestations of one Lorentz-covariant
entity. Click here for a more
detailed story.
It is gratifying to note that the entanglement series becomes
a squeezed Gaussian function which then leads to the language of
squeezed circles.
- The word "entanglement" is highly contagious these days. If you are
infected, you are OK. You are now entangled with
Einstein.
Y.S.Kim (May 2016)
- In 2019, I published the following papers telling that Einstein's E = mc2
can be derived from the Heisenberg brackets.
- Einstein's E = mc^2 derivable from Heisenberg's Uncertainty Relations,
with Sibel Baskal and Marilyn Noz,
Quantum Reports [1] (2), 236 - 251 (2019),
doi:10.3390/quantum1020021.
ArXiv. For pdf with sharper images,
click here.
- Role of Quantum Optics in Synthesizing Quantum Mechanics and Relativity,
Invited paper presented at the 26th
International Conference on Quantum Optics and Quantum Information
(Minsk, Belarus, May 2019).
ArXiv. For pdf with sharper images,
click here.
- Poincaré Symmetry from Heisenberg's Uncertainty Relations,
with S. Baskal and M. E. Noz,
Symmetry [11](3), 236 - 267 (2019),
doi:10.3390/sym11030409.
ArXiv .
Heisenberg's Gift to Einstein
Among the webpages I built on the history of physics, the page entitled
is most frequently visited. Since this page is so popular, you are invited
to visit this page again. For the same reason,
I keep adding new stories about Heisenberg's meeting with Einstein.

|
Einstein's house in Princeton.
|
|
- In 1954, Heisenberg went to Princeton to talk with Einstein, and
the meeting lasted longer than scheduled, according to Heisenberg.
However, it was not a successful meeting. After the meeting,
Einstein expressed his displeasure to his personal friend named "Johanna Fantova."
Click here for the story.
- Why did Heisenberg fail to make Einstein happy? The answer is
very simple. He was not able to tell a story Einstein wanted to hear.
Heisenberg was aware that Einstein did not like his interpretation
of the Poisson brackets. However, he could have made Einstein happy
by telling him the Poisson brackets lead to Einstein's relativity.
He could not tell this because he was not aware of this in 1954.

|
How did this young man become so close to Wigner? He told the stories Wigner
wanted to hear.
|
- In 1987, I surprised many people by publishing a paper with Eugene Wigner.
Wigner was known as one of the most difficult persons to approach, and
he was totally isolated from his colleagues at Princeton's physics department.
However, I was able to tell him the story he wanted to hear.
The story goes like
this.
- Einstein got his Nobel prize in 1921, but not for his mc2.
- Wigner got his prize in 1963, but not for
his 1939 paper on internal space-time symmetries
- It is generally agreed that Einstein deserved one full Nobel for his mc2.
Likewise, Wigner deserved one full prize for his 1939 paper, and I showed him
the following table.
Contents of Einstein's E = mc2
|
Particle |
Massive/Slow |
between |
Massless/Fast |
|
| Einstein |
Energy
Momentum |
E = p2/2m |
E =
[m2c4 + (cp)2]1/2 |
E = cp |
|
| Wigner |
Helicity
spin, Gauge |
S3
S1
S2
|
Wigner's
Little Groups |
Helicity Gauge Trans.
|
|
This table is from
one of my papers published in 1986.
- Let us go back to the Heisenberg issue. Heisenberg could have
made Einstein by telling his E = m2 is a consequence
of the symmetries derivable from his uncertainty commutation relations.
He did not know this in 1954, but he could have said this based on a
paper I published in 2019,
with Sibel Baskal and Marilyn Noz.
-
Here comes the key question. Did you know the Poisson brackets
lead to the Lorentz group? Don't worry. I am not the first person
who observed this. It was Paul A. M. Dirac who used two harmonic
oscillators to derive the group of Lorentz transformations. Dirac
in fact derived two coupled Lorentz groups or O(3,2) group starting
from two oscillators.

|
Both Dirac and Heisenberg were interested in the Poisson brackets.
Einstein did not like Heisenberg's interpretation of those brackets.
On the other hand, Dirac was interested in extending those brackets to
Einstein's Lorentz-covariant world.
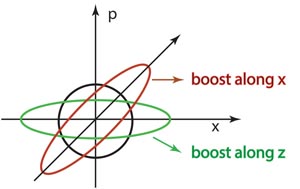
It is not clear whether they knew the Poisson bracket for a single pair
of position and momentum variables has the symmetry of the Sp(2) group
isomorphic to the Lorentz group applicable to two space-like and one
time-like directions, as specified in this figure.
|
|
|
In his 1963 paper, Dirac considered two harmonic oscillators and constructed
the following ten operators.
|
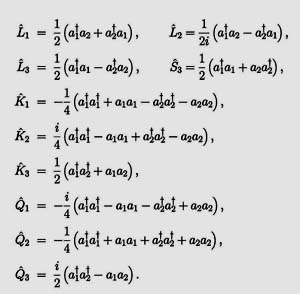
|
Dirac then noted that these operators satisfy the algebra for the generators for
the O(3,2) deSitter group, with O(3,1) as a subgroup with three rotation and
three boost generators applicable to the Monkowski space of (x, y, z, t).
The O(3,2) group requires an extra time variable. There are thus three additional
boost generators with respect to this new time variable. In addition, there is
a rotation generator for these two time variables. There are thus four
additional generators.
|

|
The issue is then to transform these four extra generators into the four space-time
translation generators the Minkowski space.
|
|
Dirac published this result in 1963 in the
Journal of Mathematical Physics. This paper
is largely unknown to the present generation of physicists, in spite of the
fact that it provides the mathematical base for many branches of physics,
including squeezed states, entanglements, entropy, high-energy physics,
Bogoliubov transformation in superconductivity, O(3,2) supersymmetry,
and presumably many future theories..
- Then, while you did not know, how do I know about this paper? In
the fall of 1962, spent many hours with Dirac. How did this happen?
Click here for a story. At
that time, I did not like what was going on the physics world.
Click here to see how much I disliked
the physics environment at that time. I had to be born again, like
Nicodemus after seeing Jesus (Bible story from the Gospel of John).
Dirac's 1963 paper is difficult to read, because it consists of a
mathematical poem consisting of ten generators and thus sixty commutation
relations. It is fun to provide interpretations to this poem using
physical examples, and this has been my research line for many years.
- Then, what does this have to do with Heisenberg? If Dirac got the
Lorentz group from the commutation relations for harmonic oscillators,
there must be the basic element of Lorentzian symmetry in Heisenberg's
Poisson brackets. Indeed, this symmetry is well known, and it is called
the group of canonical transformations.
The Poisson bracket consists of two conjugate variable x and p.
This bracket is invariant under rotations in the phase space of those two
variables. It is also invariant when x increases while p decreases while
the product xp remains constant. This is a squeeze in phase space. These
operations are enough to construct the Lorentz group applicable to the two
space-like and one time-like directions.
This symmetry is not rich enough address the symmetries in the
Minkowski space of three space-like and one time-like dimensions.
Dirac in 1963 was able to construct his richer symmetry using
two Poisson brackets. Yes, Einstein could have shown his interest
in this symmetry of the Poisson brackets, but he did not.
- The rotation in the phase space of x and p leads to the rotation around
y axis in the three-dimensional space. The squeeze along the x~p
directions leads to the Lorentz boost along the z direction. The squeeze
along the 45-degree direction corresponds to the Lorentz boost along the
x direction as shown in this figure.
- While the Poisson bracket for a single pair of position-momentum variable
leads to the Lorentz group applicable to two space-like and one time-like
directions, Paul A. M. Dirac considered two harmonic oscillators. Each
oscillator corresponds to one Poisson bracket. He then ended up with
the O(3,2) symmetry which corresponds to the Lorentz group applicable to
three space-like dimensions and two time-like directions.
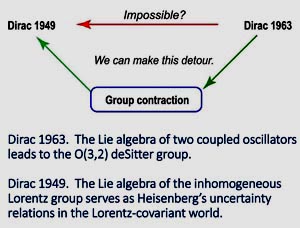
- We are familiar with the procedure of contracting the Lorentz group O(3,1)
to the Galilean group, which includes three rotations and three translations.
Likewise, we can contract O(3,2) into the Lorentz group O(3,1) and four
translation in four-dimensional Minkowski space (x, y, z, t). This group
is known as the inhomogeneous Lorentz group which serves the basic
symmetry group of quantum mechanics in the Lorentz covariant world.
You may click here for a comprehensive
discussion of this matter.
|
| |