100 Years of Continuous History since Bohr and Einstein

  • What do they say about me?

    1. Video from the Marquis Who's Who.

    2. Video from the IAOTP (International Association of Top Professionals).

From Bohr/Einstein to Gell-Mann/Feynman, and then to Entanglement

    You may click on each figure to enlarge it.


  • Paul A. M. Dirac (1902-84) was the first one to worry about how the hydrogen atom looks to moving observers.



    1. In 1927, Dirac pointed out that the c-number time-energy uncertainty relations should play a role in making the uncertainty relations in the Lorentz-covariant world.

    2. In 1945, Dirac attempted to use the four-dimensional Gaussian function to construct a wave function that can be Lorentz-boosted.

    3. In 1949, Dirac considered possible forms of quantum mechanics in the Lorentz-covariant world. He introduced his light-cone coordinate system showing that the Lorentz boost is a squeeze transformation in the the two-dimensional space of longitudinal and time-like variables.

    4. In 1962, I was a freshman assistatant professor at the Univ. of Maryland, and served as the personal assistant for Dirc when he visited the University for one week. I learned physics from him, even though I was not aware of the contents of the above-mentioned papers published by Dirac.

    5. Click here for a detailed story of my meeting with Dirac.

  • We all respect Dirac, and his papers are like poems. However, have you seen any diagrams in his books and papers? He was not like Feynman who was an exceptional cartoonist: Feynman diagrams.

  • It is thus fun to translate Dirac's papers mentioned above into cartoons. Then it is quite natural to perform a Hegelian synthesis to construct a picture of a Lorentz-covariant picture of a localized entity as shown here.

    However, during the period of Einstein, Bohr and Dirac, the hydrogen atom moving with a relativistic speed was unthinkable.

After 1950,

  • the physics world was able to produce a large amount of protons moving with a speed close to that of light. In addition, like the hydrogen atom was bound to have a non-zero radius.

  • This led Gell-Mann to formulate the quark model in 1964. The proton, like the hydrogen atom, is a bound state of more fundamental particles called "quarks." Thus, the proton inherits the bound-state quantum mechanics from the hydrogen atom.

  • Unlike the hydrogen atom, the proton can be accelerated and its speed can can become very close to that of light. Indeed, in 1969, Feynman observed that the fast moving proton appears like a collection of partons with the following peculiar properties.

    1. As the hadron moves fast, the quark distribution becomes concentrated along one of the light-cone axes. The amplitude of the oscillation becomes larger, indicating that the spring constant appears to become weaker. The particles become free!

    2. The momentum distribution becomes also widespread. This is what we see in the world through Feynman's parton model.

    3. The number of partons is infinite because free particles have continuous momentum distribution as in the case of black-body radiation.

    4. The major axis of the ellipse measures the period of oscillation. As Feynman observed, the interaction time between the quarks is dilated.

    These properties can be translated into the following figure.


    Click here for a detailed explanation of this figure.


Indeed, the bound-state quantum mechanics and special relativity can be synthesized. Thus, we can venture to ask whether Einstein's Lorentz covariance and the Heisenberg brackets share the same mathematical base.

  • The single variable Heisenberg bracket shares the same symmetry property with that of the classical Poisson bracket. We can demonstrate this most effectively using the Wigner function for the ground-state oscillator defined over the two-dimensional space of position and momentum.

    We can describe this Gaussian distribution using a circle around the origin of the two-dimensional space of x and p. The amount of the fundamental uncertainty is the area of the circle. The rotation of this circle does not change the area, neither does the squeeze.

  • Human brains are not configured to realize that the circle is a special case of the ellipse. It took 1000 years for humans to realize the orbit of the sun or earth is elliptic. It took many years for physicists appreciate this kind of transformation. The rotation plus squeeze is called "symplectic transformation." This word was used first by Hermann Weyl in his book entitled Classical Groups published in 1946 by the Princeton University Press, but Weyl introduced this word in 1931 in one of his books written in German.

    1. As late as 1986, Eugene Wigner asked me what the symplectic group is. I told him this word was introduced by Hermann Weyl. Wigner then told me he did not like Weyl. This could be the reason why the symplectic transformation is not yet widely known in the physics world.

    2. Another reason is that Goldstein in his textbook uses 40 pages to discuss transformations of the Poisson brackets. We call them canonical transformations. He mentions briefly symplect transformations. The canonoinical transformations are more professionally treated in Arnold's book entitled Mathematical Methods of Classical Mechanics.

      However, the trouble with those books is the lack of graphical illustrations. It took me several years to realize the symplectic transformation include area-preserving linear transformations.


      Mrs. Dirac was Wigner's sister.

    3. As late as 1962, while Paul A. M. Dirac was finishing up his 1963 paper on O(3,2), he was told by a younger colleague named Res Jost that what he was doing was a symplectic group. In 1962, both Dirac and Jost were at the Institute for Advanced Study in Princeton.

      In 1962, while Dirac visited the University of Maryland, I was fortunate enough to spend some time with him. I was like Nicodemus seeing Jesus (story from the Gospel of John of the New Testament). I was a confused young physicist then. Click here for a story.


    Lawrence C. Biedenharn
    (photo taken in 1988).

  • Then, do I have a brain different from other physicists? The answer is clearly NO. I did a mathematical exercise telling the circle can be continuously squeezed into an ellipse, while its area is being preserved. Click here to see how I brag about my high-school background. I once thought this deformation is all about the symplectic group and published a paper based on my limited understanding of this subject. The referee and the editor did not know what was wrong with this paper.

    Larry Biedenharn scolded me by telling me that I have to include rotations. I thank him for his guidance to the world of symplectic groups.

  • The simplest way to understand the symplectic group is to start with three two-by-two Pauli matrices:

      [sigma]y, [sigma]x, [sigma]z.

    These matrices are Hermitian, and they correspond to the three generators of the rotation group. Let us add the following three anti-Hermitian matrices.

      i[sigma]y, i[sigma]x, i[sigma]z.

    There are now six matrices. The Lie algebra of these matrics is the same as that the Lorentz group applicable to the four-dimensional Minkkowski space of (x, y, z, t). This is well known.

  • It is not yet widely known that there are three imaginary matrices among the six two-by-two matrices given above. They are

      [sigma]y, i[sigma]x, i[sigma]z.

    These imaginary matrices satisfy a Lie algebra (closed set of commutation relations) for Sp(2) group (two-dimensional symplectic group). They generate two-by-two real matrices. With them, we can do a two-dimensional geometry as shown in this figure. Furthermore, their Lie algebra is the same as that for the Lorentz group applicable to one time-like dimension and two space-like directions, also as shown in the same figure.

  • While all these can be studied in terms of the single oscillator with the Wigner function for the single oscillator, Dirac considered two oscillators, with bilinear forms of the step-up and step-down operators.


Dirac then ended up with ten operators satisfying the Lie algebra for the O(3,2) deSitter group, which is the Lorentz group applicable to three space-like and two time-like dimensions.

  • What is this deStter grouip? Let us use (x, y, z) for the space-like dimensions, and (t, s) for the time-like directions. This group is the Lorentz group applicable to the five-dimensional space of (x, y, z, t, ).

    This O(3,2) group has its own merits in general relativity and other areas of physics. Yet, we can ask whether whether

    1. this group can be constructed from the Heisenberg brackets for his uncertainty principle,

    2. this group can be transformed into other symmetry problems in physics.

    With these questions in mind,


      Lie algebra for the O(3,2) group.
    1. we can consider two Lorentz subgroups applicable to (x, y, z, t) and (x, y. z, s) respectively. Let us use Li for rotation generators applicable to (x, y, z), and use Ki for the three boost generators with the time variable t. They are the six generators for the Lorentz group familiar to all of us.

    2. There are four additional generators involving the extra time variable s. We can use Qi for the boost generators with respect to time time-like variable s instead of t. In addition, there is one rotation generator S3 which mixes up the s and t time-like variables.

    3. These ten generators constitute a closed set of commutation relations (Lie algebra) for the O(3,2) group.


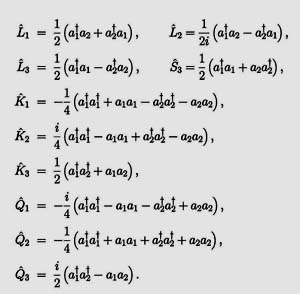
    These operators satisfy the Lie algebra of the O(3,2) group. Clearly this algebra is derivable from the Heisenberg brackets.

  • Dirac, in his paper of 1963, constructed the same Lie algebra of O(3,2) using the step-up and step-down operators for two harmonic oscillators, and these generators are given in this table. The question still is whether this group can be transformed into other symmetry problems in physics.

    To address this question, let us go to Dirac's earlier paper entitled Forms of Relativistic Dynamics Published in 1949. In this paper, he sates that the task of constructing quantum mechanics in the Lorentz-covariant world is constructing a representation of the inhomogeneous Lorentz group (Lorentz transformations in the three-dimensional space with one time variable) plus four translation generators applicable to the four-dimensional Minkowski space of (x, y, z, t) .

  • The problem is then to leave the generators Ji and Ki intact, but transform Qi and S3 into four translation operators. This is not a difficult problem. We can use the group contraction procedure to achieve this purpose.

    In 2019, I was fortunate enough to write the following three papers on this subject.

    1. Einstein's E = mc2 derivable from Heisenberg's Uncertainty Relations,
      with Sibel Baskal and Marilyn Noz,
      Quantum Reports [1] (2), 236 - 251 (2019),
      doi:10.3390/quantum1020021.
      ArXiv. For pdf with sharper images, click here.

    2. Role of Quantum Optics in Synthesizing Quantum Mechanics and Relativity,
      Invited paper presented at the 26th International Conference on Quantum Optics and Quantum Information (Minsk, Belarus, May 2019).
      ArXiv. For pdf with sharper images, click here.

    3. Poincar� Symmetry from Heisenberg's Uncertainty Relations,
      with S. Baskal and M. E. Noz,
      Symmetry [11](3), 236 - 267 (2019),
      doi:10.3390/sym11030409.
      ArXiv.

    In dealing with O(3,2) problems, we have to use many five-by-five matrices, and they are cumbersome. The problem is how to translate them into the language of two-by-two matrices.

The squeezed Gaussian function plays the pivotal role quantum optics and entanglement problems.





  • The above figure and series expansion are clearly for the two-photon coherent state. This figure tells clearly why this two-photon state is called "squeezed state." This mathematics is a product of the Lorentz group, as illustrated in this figure.

  • This mathematics is in the current literature called the Gaussian entanglement.

  • The concept of the entanglement was first formulated by Richard Feynman. In his book on statistical mechanics (1972), Feynman says

    When we solve a quantum-mechanical problem, what we really do is divide the universe into two parts - the system in which we are interested and the rest of the universe. We then usually act as if the system in which we are interested comprised the entire universe. To motivate the use of density matrices, let us see what happens when we include the part of the universe outside the system.

    Feynman then used the density matrices and Wigner functions to illustrate his rest of the universe. However, he used only one oscillator to illustrate what he said about the rest of the universe. Yes! The harmonic oscillator is the basic tool to illustrate the Wigner function. But how could he explain two different worlds with one oscillator? Go to this paper for clarification.

  • The following figure explains that time-separation variable is not measurable, and thus it belongs to the rest of the universe. In the physics of two photons, they are entangled in the squeezed state, one of them is in the rest of the universe if we do not measure it.

    This figure serves also the case of two-photon coherent state where one of the photons is not measured.


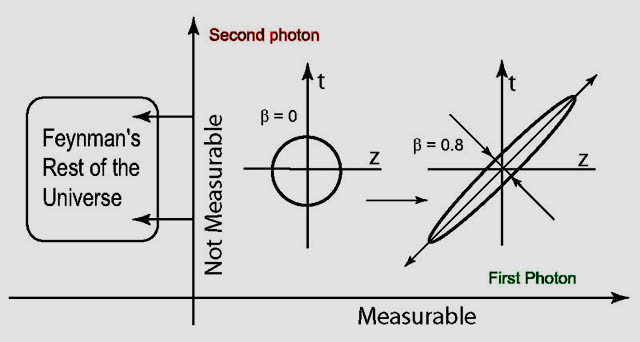
    You may click here for a detailed explanation of this figure.