Einstein Story

  • In 1905, Einstein formulated his special theory of relativity resulting in his

      E = mc2 ,

    while he was working for the Swiss patent office in Bern, Switzerland.


        Einstein's condo in Bern, Switzerland.

        Einstein's house in Princeton, NJ, USA.

    1. Click here for Einstein's Bern.

    2. While Einstein was a high-school student, he became keenly interested in the philosophy of Immanuel Kant, which says things could appear differently depending on the observer's environment and status of mind. Click here for further illustration.

      Einstein became interested in how things appear to moving observers. However, there were no objects moving fast enough to exhibit this relativistic effect, except some cosmic rays coming from the outer space. However, there were no detection technique available at that time.

    3. Presumably, in order to find observable effects, Einstein started studying gravitational effects on light lays in 1908. This became the beginning of his general theory of relativity, worrying about the universe and far-away places.

  • Let us come back to the events which can be observed on the surface of the world.

      Bohr and Einstein, photo from the AIP Visual Archives.

  • One hundred years ago, Bohr and Einstein met occasionally to discuss physics. Bohr was worrying about why the energy levels of the hydrogen atom are discrete, while Einstein was interested in how things look to moving observers. Did they ever discuss how the hydrogen atom looks to a moving observer?

  • Bohr's worry became the present form of quantum mechanics where the hydrogen atom is a quantum bound state or a standing wave. Thus, the problem becomes that of a

      moving bound state
      in Einstein's world.

    In Einstein's world, moving objects appear differently according to Lorentz transformations. Click here for illustrations.

  • While there are no observable hydrogen hydrogen atoms moving with relativistic speeds (speed comparable with the light speed), modern accelators started producing protons with relativistic speed, after 1950. The question is then what does the proton has to do with bound states like the hydrogen atom.

  • According to Gell-Mann (1954), the proton at rest is a bound state of three quarks . According to Feynman (1969), the proton moving with the velocity close to that of light appears as a collection of an infinite number partons. Are they talking about the same proton? This question is illustrated in this figure:

  • Click here for the resolution of the quark-parton puzzle. For the moving bound state, it is possible to construct the harmonic oscillator wave functions that can be Lorentz-boosted. We can call them Covariant Harmonic Oscillators and construct the following table.

    Einstein's World

    		Massive/Slow between Massless/Fast
    Energy
    Momentum     		E=p2/2m Einstein's
    E=(m2 + p2)1/2
    		E=p
    Hadrons,
    Bound States     		Gell-Mann's
    Quark Model    		 Covariant
    Oscillators     		Feynman's
    Parton Picture

  • The question then is how to construct the Lorentz-covariant harmonic oscillator wave functions. Paul A. M. Dirac made his life-long efforts to construct Lorentz-covariant ocillator wave functions. We can mention the following four papers.

    1. P. A. M. Dirac, The Quantum Theory of the Emission and Absorption of Radiation, Proc. Roy. Soc. (London) A [114], 243 - 265 (1927).

    2. P. A. M. Dirac, The Quantum Theory of the Emission and Absorption of Radiation, Proc. Roy. Soc. (London) A [A183], 284 - 295 (1945).

    3. P. A. M. Dirac, Forms of Relativistic Dynamics, Rev. Mod. Phys. [21] 392 - 399 (1949).

    4. P. A. M. Dirac, A Remarkable Representation of the 3 + 2 de Sitter Group, J. Math. Phys. [4], 901 - 909 (1963).

    I had the privilege of meeting Dirac in 1962 and learn his physics directly from him. His papers are like poems and enjoyable to read. However, his papers do not contain figures or illustractions. Another problem is that Dirac never quotes hiw own papers published earlier on the same subject. Presumably, he thought he was presenting new ideas when he wrote those papers.

    We can thus translate his pictures into cartoons and combine those cartoons. The net result is

    This ellipse (squeezed circle) can provide the resolution of the quark-parton puzzle and thus the Bohr-Einstein issue. Click here for a detailed story.

    For a published papers on this subject, go to

    1. Integration of Dirac’s Efforts to Construct a Lorentz-covariant Quantum Mechanics,
      with Marilyn E. Noz.
      Symmetry [12(8)], 1270 (2020),
      doi:10.3390/sym12081270,

    2. Physics of the Lorentz Group, Second Edition: Beyond High-energy Physics and Optics,
      with Sibel Baskal and Marilyn Noz,
      to be published by the IOP (British Institute of Physics).




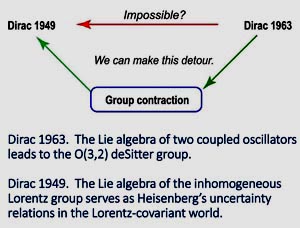
  • As for Dirac's 1963 paper on the two-oscillator sysem, he constructed a Lie algebra (closed set of commutation relations for the generators of the group) for the Lorentz group applicable to three space-like dimensions and two time-like dimensions. This group is known as the O(3,2) deSitter group.

    The remarkable fact is that this set was constructed solely from Heisenberg's brackets for his uncertainty relations. How is it possible to derive a set of equations for Einstein's relativity from those for quantum mechanics?

    The remaining question is to transform the second time variale of the O(3,2) system into a useful variable in the Minkowskian system of three space coordinates and one time. Indeed, it is possible through the group contration techique. I published a number of papers on this issue.

    1. Poincaré Symmetry from Heisenberg's Uncertainty Relations,
      with S. Baskal and M. E. Noz,
      Symmetry [11(3)], 236 - 267 (2019),
      doi:10.3390/sym11030409,

    2. Einstein's E = mc2 derivable from Heisenberg's Uncertainty Relations,
      with Sibel Baskal and Marilyn Noz,
      Quantum Reports [1(2)], 236 - 251 (2019),
      doi:10.3390/quantum1020021,

    3. Physics of the Lorentz Group, Second Edition: Beyond High-energy Physics and Optics,
      with Sibel Baskal and Marilyn Noz,
      to be published by the IOP (British Institute of Physics).


  • What do they say about me?

    1. Video from the Marquis Who's Who.

    2. Video from the IAOTP (International Association of Top Professionals).


Two more fundamental issues

  • A massive particle at rest has three rotational degrees of freedom. However, a massless particle has only one degree of freedom, namely around the direction of its momentum. What happens to rotations around the two transverse directions when the particle is Lorentz-boosted?

  • You also have been wondering why massless neutrinos are polarized, while massless photons are not.

    The answers to these questions are in the bottom row of this table:

    Einstein's World

    		Massive/Slow between Massless/Fast
    Energy
    Momentum     		E=p2/2m Einstein's
    E=(m2 + p2)1/2
    		E=p
    Hadrons,
    Bound States     		Gell-Mann's
    Quark Model    		 Covariant
    Oscillators     		Feynman's
    Parton Picture
    Helicity
    Spin,Gauge     		S3
    S1 S2     		Wigner's
    Little Group     		Helicity
    Gauge Trans.
    Click on the colored items for further explanations.

  • If you are interested in symmetry problems, you should be aware that Wigner's 1939 paper deals with the subgroups of the Lorentz group whose transformations leave the momentum of a given particle invariant. Thus, these subgroups dictate the internal space-time symmetry of the particle.

    It is generally agreed that Wigner deserved a Nobel prize for this paper alone, but he did not. He got the prize for other issues. Click here for my explanation of where the confusion was. Wigner liked my story. This is the reason why he had photos with me, and I am regarded as Wigner's youngest student, even though my thesis advisor at Princeton was Sam Treiman.

  • I did enough work for Wigner to deserve this genealogy:

    and to expand my scope of research.


Lorentz Group in Other Branches of Physics

    The Lorentz group is the mathematical language for Einstein's special relativity. Two-by-two matrices are everywhere in physics, and they are representations of the Lorentz group. Thus, the mathematical language from this group serve useful services in other branches of physics. Modern optics is a case in point.

  • If you like modern optics, including coherent and squeezed states, beam transfer matrices, polarization optics, as well as periodic systems, click here.

    1. If you are interested in entanglement problems, particularly Gaussian entanglements, click here.

    2. If you are interested in entropy problems and Feynman's rest of the universe, click here, and here.

    3. Poincaré and Einstein? click here, and here.

    4. Poincaré sphere for polarization optics and the Poincaré symmetry for Einstein's relativity. Click here.

  • I am now working the Lorentz group in condensed matter physics.

Acknowledgments

    This page is based on the papers I published since 1973. I wrote many of those papers in collaboration with a number of co-authors, especially, Sibel Baskal, Elena Georgieva, Daesoo Han, Marilyn Noz, Seog Oh, and Dongchul Son. Michael Ruiz and Paul Hussar were my graduate students. They made key contributions to this program. I would like to thank them.

    I am grateful to Professor Eugene Wigner for clarifying some critical issues concerning his 1939 paper on the internal space-time symmetries of particles in the Lorentz-covariant world. Click here f or my webpage dedicated to Eugene Paul Wigner.