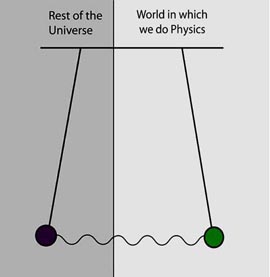
Feynman's Rest of the Universe

Do you know how to do quantum mechanics of this system?

When we solve a quantum-mechanical problem, what we really do is divide the universe into two parts - the system in which we are interested and the rest of the universe. We then usually act as if the system in which we are interested comprised the entire universe. To motivate the use of density matrices, let us see what happens when we include the part of the universe outside the system.

Feynman then used the density matrices and Wigner functions to illustrate his rest of the universe. However, he used only one oscillator to illustrate what he said about the rest of the universe. Yes! The harmonic oscillator is the basic tool to illustrate the Wigner function. But how could he explain two different worlds with one oscillator?

• It appears that the best way to understand what Feynman said above is to use two coupled harmonic oscillators. One of them is in the world in which we do physics, and the other is for the rest of the universe. It is straight-forward to construct the Hamiltonian for the system of two coupled oscillators. It is not difficult to construct wave functions, density matrices, as well as Wigner functions for this two-oscillator system.

  Then there is a well-established procedure for constructing the density matrix and Wigner function when one of the two oscillators is not observed: to sum over or integrate out the un-observed variable. The net result is the increase in entropy through the density matrix, and an addition of statistical uncertainty through the Wigner function.

• However, it was difficult for me and my co-authors to publish the paper saying this. The reason is very simple. The referees kept saying the paper is too trivial, but the truth was that they did not like my research group becoming more famous than they are by talking about Feynman. This is the Herod complex shared by all physicists.

  It took us eight years to publish, and it appeared finally in the American Journal of Physics in 1999. The final referee said the paper is right and appropriate for the journal, but he could not recommend publication. He did not explain why. The editor over-ruled the referee's Herod complex after our appeal.

• Click here for the article using two oscillators to illustrate Feynman's rest of the universe. One oscillator for the world in which we do physics, and the other for the rest of the universe.

• Not many people know about this. Then, how do I know? I talked with Dirac in 1962. Click here to see how it happened.

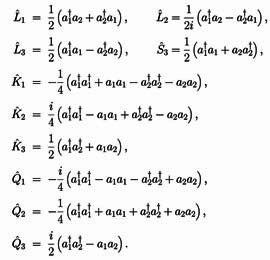
  Dirac's poem on two oscillators. Can you translate this poem to the language of physicists?

• Another reason is that Dirac in his paper uses the mathematics known as the O(3,2) deSitter group for two coupled Lorentz groups, and the Sp(2) group for the four-dimensional phase space for the two oscillators. Physicists do not like to study these groups each with ten generators.

  In addition, these groups also deal with squeeze transformations. Physicists do not like to worry about transformations other than orthogonal or unitary.

• Dirac noted that there are ten generators of those groups, and he wrote down them in the language of step-up and step-down operators. Click here for those operators. We all know these operators can be used for the creation and annihilations in the Fock space. Thus, Dirac was the earliest person to work out the symmetries of two-photon or squeezed states.

• With this preparation, we can become ambitious enough to tackle the problem of hidden variables in quantum mechanics. The question is whether they are hidden in Feynman's rest of the universe.

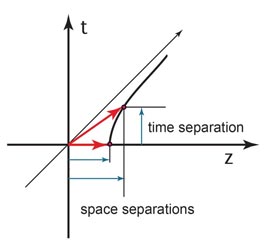
The time Separation is hidden in Feynman's Rest of the Universe.

They could have talked about the Lorentz-boosted Bohr radius, but we do not know anything about their conversation if it took place. Thus, the time separation is a hidden variable in the present form of quantum mechanics.

• Niels Bohr is also well known for his Bohr radius. To him, the proton was sitting at the center of the universe, even though he knew the existence of the time variable associated with the space. Einstein perhaps thought about the hydrogen atom in a moving frame, but he never said anything about it. His Lorentz transformations are strictly for point particles.

  If they did not talk about this, they are excused. Physics is an experimental science. The hydrogen atom moving with a relativistic speed was was not in the scope of physicists.

  It is still unthinkable for the hydrogen atom to move with a relativistic speed, but the proton can be accelerated to a speed very close to that of light. The question then is whether the proton has it own quantum mechanics like the hydrogen atom. Yes, the quark model formulated in 1964 could tell the story. We can therefore illustrate the evolution of the hydrogen atom has gone through with this figure.

  Needless to say, this evolution was made possible thanks to the advances in the accelerator physics. At the proton proton speed of 0.9999999999c. At magnitude of time separation is essentially the same as that of the spacial separation.

  In order to study this hidden variable, I spent many years with Marilyn Noz. We published many papers, but we also had many problems with the referees, because the time-separation variable is thoroughly hidden to them.

• Feynman talking at the APS meeting in 1970. The conference room was dark during his presentation. I was there to take this photo.

  The first person who recognized the existence of this variable was Richard Feynman. Based on his talk given at the 1970 APS spring meeting, he published his paper with his students in Phys. Rev. D 3 , 2706 (1971)]. In this paper, Feynman et al. state the existence of the time-separation variable. They said they could not do anything about this variable because they do not anything about it. I like very much their honest statement, but this is not we expect from Feynman. With my colleagues, I fixed this problem in this JMP paper.

  Earlier, in 1969, Feynman noted that the proton with an ultra relativistic speed looks like a a collection of partons whose properties are quite different from those of the quarks for the proton at rest. Click here for Feynman's parton picture.

  The point is that Dirac's two-oscillator system tells about both quantum mechanics and relativity. Thus, it can contains the Lorentz-boosted harmonic oscillators.

  Dirac's two-oscillator system also explains canonical transformations of two-oscillator system in the four-dimensional phase space. As I said before, I enjoy translating Dirac's poems into Feynman's language (cartoons). Click here how this is possible.

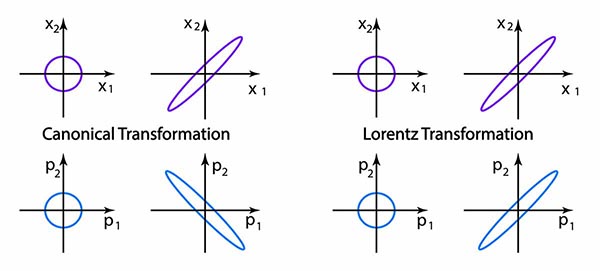
  Let me summarize Dirac's i963 paper into the following cartoon.

  

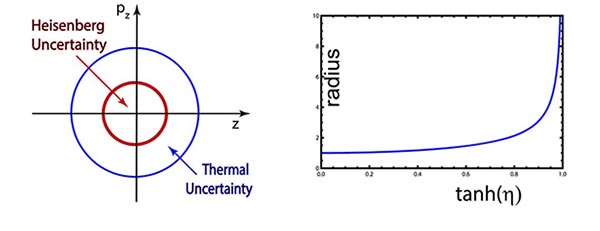
  For two oscillators, we are led to consider two-variable Gaussian function. If there is no coupling between them, each function is a circle. If the coupling becomes stronger each circle become squeezed into an ellipse.

  The quantum mechanics of the coupled oscillator is well defined, but we do not know anything about the time separation variable in the quantum world. In this figure, we can assume that x₁ is the world in which we do physics, while x₂ belongs to Feynman's rest of the universe.

  In the Lorentz-covariant world, we use the variables z and t, instead of x₁ and x₂. We thus end up with the following figure.

  

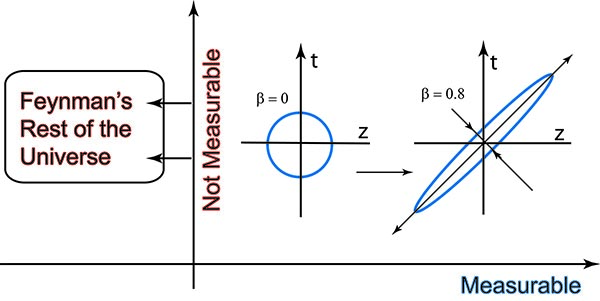
  There is a well-defined procedure for constructing density matrices and Wigner functions for phase space. The density matrix leads to the entropy caused by the variables we cannot measure (belonging to Feynman's rest of the universe), while the Wigner function gives the phase-space picture of the additional uncertainty, as shown in this figure.

  

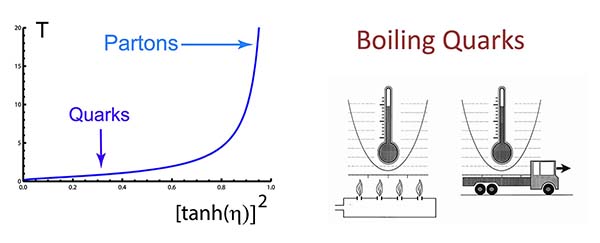
  As for the entropy, see the following figure. The entropy increase in the oscillator system means the temperature increase, as indicated in the following figure.

  

• Yes, there are published papers containing formulas for these figures. Click here for one of those papers.

I still have to proof-read this page thoroughly. Like you, I am a busy person. I hope I will be able to clean up the mess soon.