|
Why three? |

|

|

|
Click here for detailed references. |
Dirac
|
Wigner
|
Feynman
|
| Major contributions | c-number time-energy uncertainty, harmonic oscillators, light-cone coordinate system. | Little groups defining internal space-time symmetries. | Parton model, oscillator model for Regge trajectories, in addition to Feynman diagrams. |
| Favorite language | Poems. Dirac's writings are like poems. | Group theory, and two-by-two matrices. | Diagrams and pictures. |
| Soft spots |
Lack of figures and illustrations. Lack of physical examples. Before the age of high-energy accelerators. |
Lack of concrete physical examples. His 1939 paper could not explain Maxwell's equations. | He could not explain his parton picure in terms of the mathematical tools developed by Dirac and Wigner. |
|
Mathematical Instruments |
Dirac's idea is to use the Gaussian function (the language of quantum mechanics) for the circle.
|
|
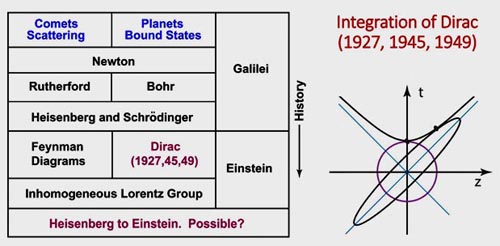
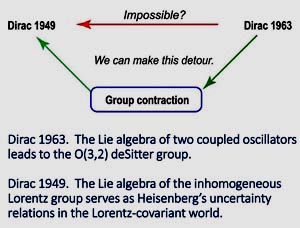
If we integrate those nine papers by Dirac, Wigner, and Feynman, we end up with Further Contents of Einstein's E = mc2.
|
|
We can now be more ambitious.
|
copyright@2021 by Y. S. Kim, unless otherwise specified. The color photo of Dirac by Bulent Atalay, and photo of Wigner by Y. S. Kim (1988). Feynman's photo is from the main lobby of the Feynman Computing Center at the Fermi National Accelerator Laboratory, Batavia, Illinois, USA.