|
|
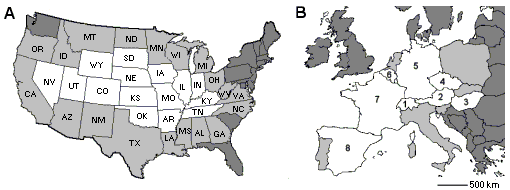
Fig. S9. Macroeconomic commodity-flow networks. (A) U.S. interstate commodity flow.(10) The central 15 states (white), along with the surrounding edge-zone of 19 immediately contiguous states (light gray), were analyzed. Core and edge areas for USA15 states are listed in Table S5 connection matrix below. (B) European international commodity flow.(11) The central 8 countries (white), along with a fragmentary surrounding edge-zone of 6 immediately contiguous countries (light gray), were analyzed as pilot data.
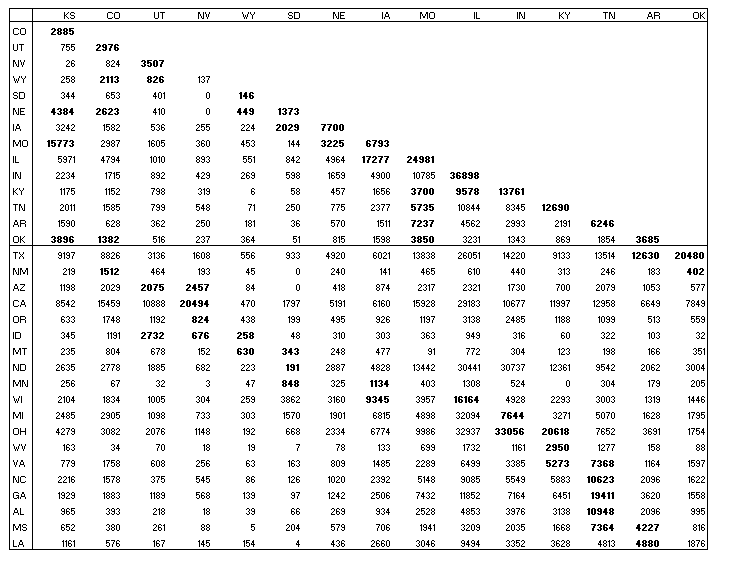
Table S5. Combined "connection" and adjacency matrix for U.S. interstate commodity flow (1997 Survey Sample). The series of 15 core states shown above in Fig. S9A is listed (KS - OK), in the order in which the areas are successively added to the analysis. They are followed by the set of 19 edge states for the total core (TX - LA). Cell values are in $ millions. An all-or-nothing cutoff threshold was set to yield approximately the same connectivity density as macaque and cat cortex above (see Table S7): If "export" + "import" flow between two states exceeds $ 1,500,000,000, a connection is recorded; sub-threshold economic transactions between the state of a row and the state of a column count as no connection. Cell values in bold designate topological contiguity of the two states, as in Fig. S9A.

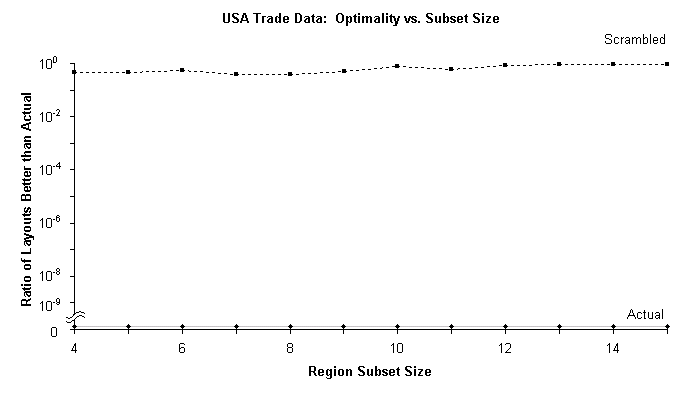
Fig. S10. Size Law performance for commodity flow among 15 U.S. states (BTS). The system of components here is a core of contiguous economic zones as in Fig. S9, with "connections" and adjacencies as in Table S5. For evaluation of how well total interconnection costs are minimized, optimality-measure is conformance of the system to the "all or nothing" adjacency rule: each layout is scored in terms of its number of violations of the rule. A series of nested compact subsets of the set of zones was generated (order of successive states added is as in Table S5). Each subset of the actual layout was compared with all possible alternative layouts of that subset for adjacency-rule optimality (14 and 15-element sets were each compared only with random samples of 109 alternative layouts).
The US system attains better connection-optimization than macaque or cat visual cortex, with no layouts better than actual found in a 1 billion sample. This may appear to vindicate the "invisible hand" of laissez-faire economics. However, the "Actual layout" curve departs markedly from the Size Law pattern; smaller subsets already attain perfect optimality--i.e., an optimality ratio of 0, with no alternative layouts better than the actual one. This breakdown suggests the macroeconomic networks are optimized locally, unlike the cortex (and some chip) networks. For calibration, the "Scrambled layout" (broken-line) curve, for the 15 U.S. states with their adjacencies randomly shuffled, shows the usual "flat" unoptimized pattern.
Copyright Christopher Cherniak (2002)
Last Modified 11/19/2002