
[Simple Example]
[Command line function] [Segmented Fourier filter] [Interactive
Fourier Filter] [Live Script Fourier filter] [Application of a narrow bandpass filter]
[Live Script
Fourier Filter]
The Fourier filter is a type
of filtering function that is based on manipulation of specific
frequency components
of a signal. It works by taking the Fourier transform of the
signal, then attenuating or amplifying specific frequencies, and
finally inverse transforming the result. In many science
measurements, such as spectroscopy and chromatography, the
signals are relatively smooth shapes that can be represented by
a surprisingly small number of Fourier components. For example,
the animation below (script) shows in
the top panel a signal of three smooth peaks, with peak heights
of 1, 2, and 3, where the x-axis is time in seconds. The middle
panel shown the first 51 frequencies of its Fourier spectrum
(zero through 50). In this case the x-axis is both the frequency
in Hz and the Fourier component number (because the duration of
the signal is exactly 1 second). The amplitude of the Fourier
components is strongest at low frequencies and drops to near
zero at 25 Hz.
The bottom panel shows in this figure the signal
re-constructed by inverse transforming the first "n" Fourier
components. The animation (visible in a web browser) shows the
result of using the frequencies between 1 through 25
progressively. The reconstructed signal starts as a single sine
wave and becomes progressively more complex as more frequencies
are added, until it is visually indistinguishable from the
original signal when 25 frequencies are included. But notice
what the reconstructed signal looks like when it gets to 16
frequencies; the amplitude has already dropped very low and
there is relatively little amplitude in the remaining
frequencies. The three peaks are rendered well but the baseline
has a distinct ripple. That is caused by the abrupt cut-off of
the frequencies beyond that point, which can be avoided by using
a filter with an adjustable filter shape that allows the cut-off
rate to be controlled.
The figure below shows the same three-peak
signal, but with the addition of random white noise with a
standard deviation equal to the the peak height of the smallest
peak (line 14 of the same script). White noise has equal
amplitude at all frequencies, whereas most of the peak
signal is concentrated in the first 25 frequencies, so we can
expect that most but not all of the noise can be eliminated by
employing a low-pass filter with a cut-off frequency around 25
Hz. The result (bottom panel) shows the three peaks with their
position and peak heights approximately intact. Obviously the
noise below 25 Hz remains, which is why the signal is
imperfect.
The optimization of the Fourier
filter for the signal-to-noise (SNR) ratio of peak signals faces
the same compromise as conventional smoothing functions; namely,
the optimum SNR is achieved when the peak height is less than
the noiseless maximum. For example, the script GaussianSNRFrequencyReconstruction.m
shows that the optimum SNR is reached when the peak height
is about half the true value, but the peak area is the
same.
Adjustable filter shape. A more dramatic
example is shown the figure below. In this case, the signal (top
left) seems to be only random high-frequency noise, and its
Fourier spectrum (top right) shows that high-frequency
components dominate the spectrum over much of its frequency
range (script). In the bottom
left figure, the Fourier spectrum is expanded in the X and Y
directions to show the low-frequency region more clearly
There, the series of relatively smooth bumps with peaks at the
1st, 20th, and 40th frequencies, are most likely the actual
signal. Working on the hypothesis that the components above the
40th harmonic are increasingly dominated by noise, a more
versatile Fourier filter function (FouFilter.m)
can be used to gradually reduce the higher harmonics and to
reconstruct the signal from the modified Fourier transform (red
line). The result after inverse Fourier transforming (bottom
right) shows the signal actually contains two partly overlapping
Lorentzian peaks that were totally obscured by noise in the
original signal.

ffty=fft(y); % ffty is the fft of y
lfft=length(ffty); % Length of the FFT
% All frequencies between n and lfft-n in
the fft
% are set to zero.
ffty(n:lfft-n)=0;
fy=real(ifft(ffty)); % Real part of the inverse fft
Here, n is the number of
frequencies that are passed; all others are simply eliminated.
The function form of this operation is flp.m.
This is the minimal essence of a Fourier filter. The script flptest.m demonstrates its use (figure on
the right). The is not really a practical filter, however,
because its abrupt cutoff usually results in ringing on the
baseline, as shown above.
General-purpose Fourier filter
function. To make the Fourier filter more generally
useful, we should add code to include not only low-pass, but
also high-pass, band pass, and band reject filter modes, plus
a provision for more gentle and variable cut-off rates. This,
and more, is done in the following section. The custom Matlab/Octave function FouFilter.m can serve as a
bandpass or bandreject (notch) filter with variable cut-off
rate. (Version 2, March, 2019, correction thanks to Dr.
Raphael Attie, NASA/Goddard Space Flight Center). It has the
form [ry,fy,ffilter,ffy] = FouFilter(y, samplingtime,
centerfrequency, frequencywidth, shape, mode), where y is the
time-series signal vector, 'samplingtime' is the total
duration of sampled signal in sec, millisec, or microsec;
'centerfrequency' and 'frequencywidth' are the center
frequency and width of the filter in Hz, KHz, or MHz,
respectively; 'Shape' determines the sharpness of the cut-off.
If shape = 1, the filter is Gaussian; as shape increases the
filter shape becomes more and more rectangular. Set mode = 0
for band-pass filter, mode = 1 for band-reject (notch) filter.
Set centerfrequency to zero for a low-pass filter. FouFilter
returns the filtered signal in 'ry'. It can handle signals of
virtually any length, limited only by the memory in your
computer. Here are two examples of its application: TestFouFilter.m demonstrates a
Fourier bandpass filter applied to a noisy 100 Hz sine wave
which appears in the middle third of the signal record. TestFouFilter2.m is an animated
demonstration of the Fourier bandpass filter applied to a
noisy 100 Hz sine wave signal, with the filter center
frequency swept from 50 to 150 Hz. Both requires the
FouFilter.m function in the Matlab/Octave path.
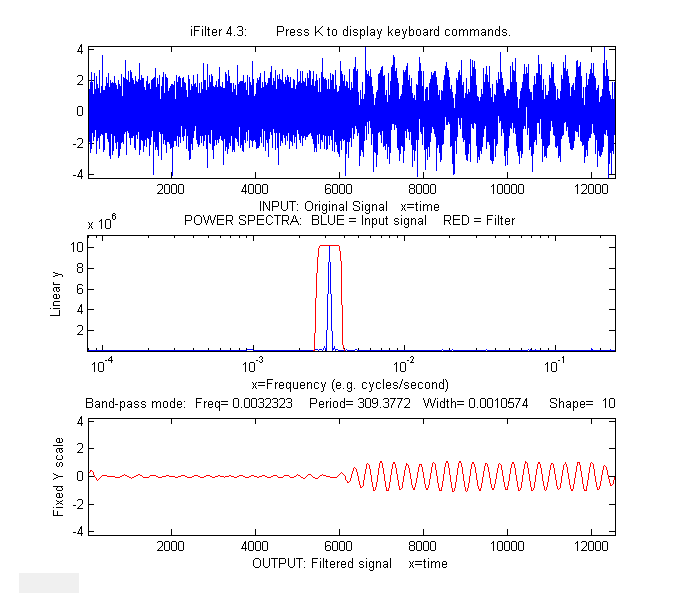 active Fourier
Filter for Matlab, allows you to select from six filter
modes ('band-pass', 'low-pass', 'high-pass', 'band-reject (notch),
'comb pass', and 'comb notch'). (In the comb modes, the filter has multiple bands located at
frequencies 1, 2, 3, 4... times the center frequency, each with
the same controllable width and shape). In each of these filter
modes, you can interactively adjust the filter parameters (center
frequency, filter width, and cut-off rate) while observing the
effect on the signal output dynamically. This is a self-contained
Matlab function that does not require any toolboxes or add-on
functions. Click here to view or
download. There is a separate version for Octave users
that uses different key for controlling filter center frequency
and width.
active Fourier
Filter for Matlab, allows you to select from six filter
modes ('band-pass', 'low-pass', 'high-pass', 'band-reject (notch),
'comb pass', and 'comb notch'). (In the comb modes, the filter has multiple bands located at
frequencies 1, 2, 3, 4... times the center frequency, each with
the same controllable width and shape). In each of these filter
modes, you can interactively adjust the filter parameters (center
frequency, filter width, and cut-off rate) while observing the
effect on the signal output dynamically. This is a self-contained
Matlab function that does not require any toolboxes or add-on
functions. Click here to view or
download. There is a separate version for Octave users
that uses different key for controlling filter center frequency
and width.
MorseCode.m is a script that uses
iFilter to demonstrate the abilities and limitations of Fourier
filtering. It creates a pulsed fixed 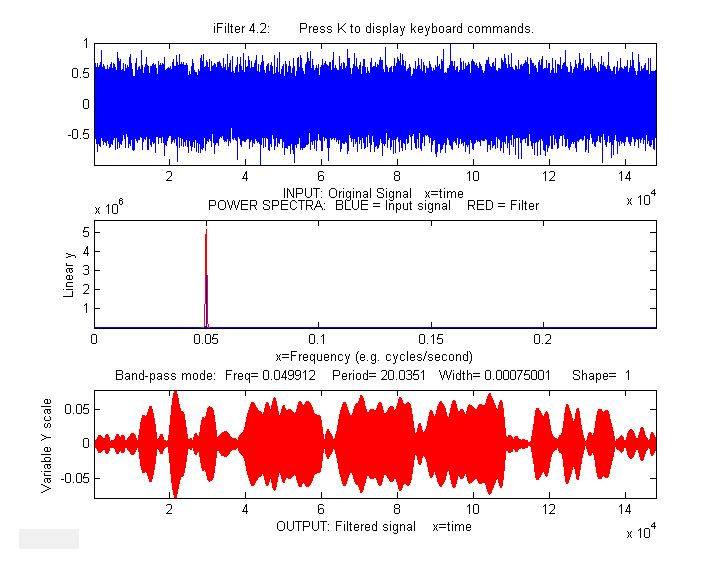 frequency (0.05) sine
wave that spells out "SOS" in Morse code
(dit-dit-dit/dah-dah-dah/dit-dit-dit), adds random white noise
so that the SNR is extremely
poor (about 0.1 in this example). The white noise has a
frequency spectrum that is spread
out over the entire range of frequencies; the signal
itself is concentrated mostly at a fixed frequency (0.05) but
the presence of the Morse
Code pulses spreads out its
spectrum over a narrow
frequency range of about 0.0004. This
suggests that a Fourier bandpass filter tuned to the signal
frequency might be able to isolate the signal from the noise. As
the bandwidth is reduced,
the signal-to-noise ratio improves and the signal begins to emerges from the
noise until it
becomes clear, but if the bandwidth is too narrow,
the step response time is too slow to give distinct "dits" and
"dahs". The step response time is inversely proportional to
the bandwidth. (Use the ? and " keys to adjust the bandwidth.
Press 'P' or the Spacebar to hear the sound). You can
actually hear that sine wave component better than
you can see it in the waveform plot (upper panel),
because the
ear works like a spectrum analyzer, with separate nerve
endings assigned to to specific frequencies, whereas the eye
analyz
frequency (0.05) sine
wave that spells out "SOS" in Morse code
(dit-dit-dit/dah-dah-dah/dit-dit-dit), adds random white noise
so that the SNR is extremely
poor (about 0.1 in this example). The white noise has a
frequency spectrum that is spread
out over the entire range of frequencies; the signal
itself is concentrated mostly at a fixed frequency (0.05) but
the presence of the Morse
Code pulses spreads out its
spectrum over a narrow
frequency range of about 0.0004. This
suggests that a Fourier bandpass filter tuned to the signal
frequency might be able to isolate the signal from the noise. As
the bandwidth is reduced,
the signal-to-noise ratio improves and the signal begins to emerges from the
noise until it
becomes clear, but if the bandwidth is too narrow,
the step response time is too slow to give distinct "dits" and
"dahs". The step response time is inversely proportional to
the bandwidth. (Use the ? and " keys to adjust the bandwidth.
Press 'P' or the Spacebar to hear the sound). You can
actually hear that sine wave component better than
you can see it in the waveform plot (upper panel),
because the
ear works like a spectrum analyzer, with separate nerve
endings assigned to to specific frequencies, whereas the eye
analyz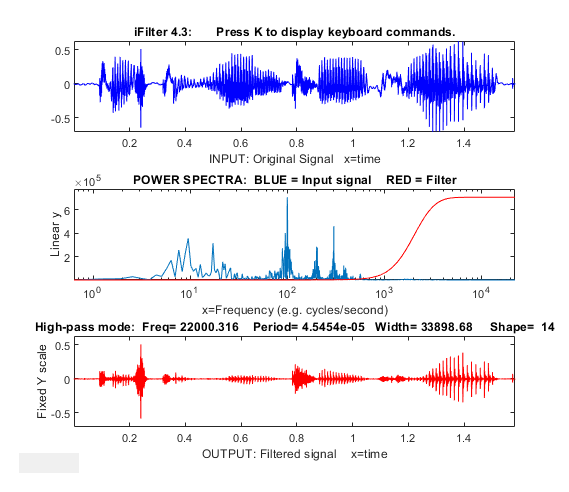 es the graph spatially, looking at
the overall amplitude and not at individual frequencies.
es the graph spatially, looking at
the overall amplitude and not at individual frequencies.
FourierFilterTool.mlx is a Live Script version of the
interactive Fourier filter iFilter.m. It can perform six
different types of Fourier filtering on your own data stored
in .csv or .xls format. The graphic display (above right) is
essentially identical to the iFilter.m function.
Note: To view the figures to the right of the
control panel as shown above, right-click on the right-hand
panel and select "Disable synchronous scrolling".
Clicking the "Open data
file" button in line 1 opens a file browser, allowing you to
navigate to your data file (in .csv or .xlsx format; the
script assumes that your x,y data are in the first two
columns; you can change that in lines 27 and 28). In the case
shown here, the data file is 'ThreeSines.csv', shown as the 'file' variable in the
Matlab workspace. The startpc and endpc
sliders in lines 5 and 7 allow you to select which portion of
the data range to process, from 0% to 100% of the total range
of the data file.
There are drop-down menus and sliders to select the
type of filter type, center frequency, filter width, filter
shape, linear or log axes, time or frequency mode, and fixed or
variable Y axis for the output.
Clicking the checkbox labeled "PlayOutputAsSound"
will send the output waveform to the system's speaker each
time any control is changed. Un-check that box to cancel.