Research Projects
Quantifying Measurement Precision
Misunderstandings of classical test theory (CTT) and reliability are common in psychometric applications. In a series of pedagogical papers, my colleagues, Drs. Jolynn Pek and Alberto Maydeu-Olivares, and I clarified that indices of measurement precision are properties of (observed or latent) scores given the population measurement model. In particular, we demonstrated that CTT reliability is the coefficient of determination from the (possibly nonlinear) regression of an observed score onto all latent variables in the model. As an alternative, we may quantifies measurement precision by the proportional reduction in mean squared error (PRMSE), which is the coefficient of determination from the (possibly nonlinear) regression of a latent score onto all response variables. We also develop a Monte Carlo procedure to approximately compute CTT reliability and PRMSE under complex measurement models.
Fiducial and Objective Bayesian Inference
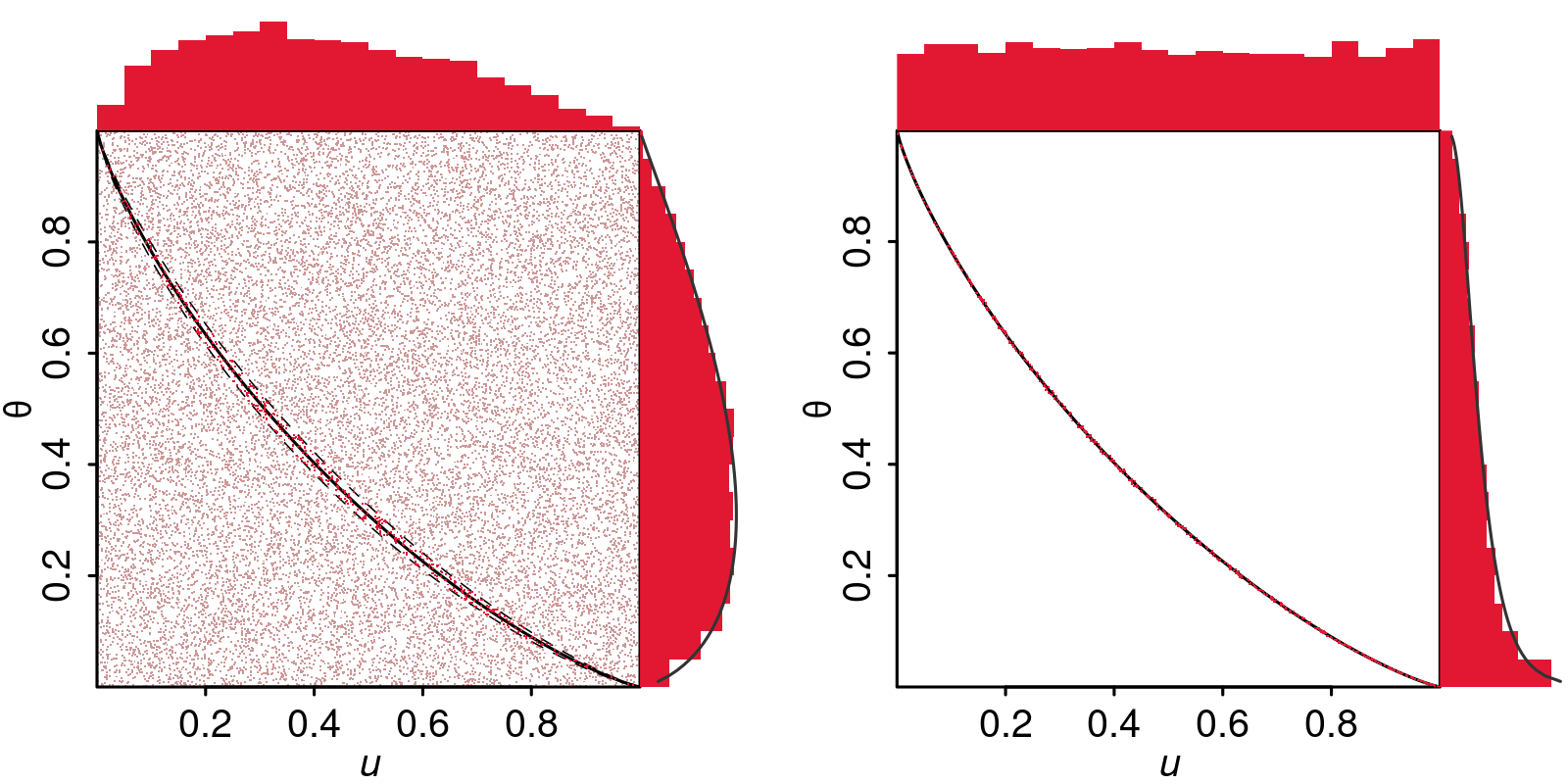
Both fiducial inference and objective Bayesian inference are well-established frameworks for prior-free statistical inference conditional on the observed data (i.e., "post-data" inference, in contrast to frequentist inference that is "pre-data"). In my previous collaboration with Dr. Jan Hannig, we found that fiducial and objective Bayesian procedures often enjoy more favorable frequentist properties compared to gold-standard frequentist methods such as maximum likelihood. We also studied the asymptotic expansion of fiducial/posterior quantiles and proposed general strategies to construct probability matching fiducial/posterior distributions, which leads to higher-order accurate confidence intervals. More recently, we proposed a unified conceptualization of post-data inference based on differential geometry. Based on the geometric characterization, we argue that fiducial inference is a natural workaround to Bayesian inference when no prior information is available.
Long-term and Daily Associations among Intersectional Minority Stress, Structural Oppression, and Alcohol Use and Misuse among Sexual Minority Adolescents of Color (NIH 7R01AA029989)
Disparities in alcohol and other substance (AOD) use and misuse are well documented among sexual minority adolescents (SMA) and their heterosexual peers. SMA of color also have higher rates of AOD use and misuse than heterosexual peers of the same race/ethnicity and to some extent their White SMA peers. Daily stigma and discrimination-related stressors specific to their marginalized identities (i.e., minority stressors, racism-based stressors) contribute to health disparities among SMA of color. These stressors occur at the interpersonal level (e.g., discrimination) and are reinforced at the structural level (e.g., anti-gay laws, or racist institutional policies). In this project, we study intersectional stress and structural oppression and how they relate to AOD use and misuse among SMA of color using a measurement burst design. Our specific aims are to: 1) test the prospective associations between intersectional stress and structural oppression and AOD use and misuse among a national sample of SMA of color over 2.5 years at a 6-month time interval; 2) test the daily associations between within-person fluctuations of intersectional stress and AOD craving, use, misuse, and problems among the sample over 10-days at each time point; 3) test protective and risk factors that attenuate or exacerbate the associations between intersectional stress and AOD use and misuse over adolescence across the 2.5 years and in daily life.
Multilevel Regression Discontinuity Design With Latent Variables
(IES R305D220030)
A regression discontinuity (RD) design is often employed to provide causal evidence when a randomized control trial is practically infeasible or unethical. Conventional RD models assume that all running variables, covariates, and outcomes are observed variables. The purpose of this grant is to extend the modeling framework to augment the structural RD model with multilevel latent variable measurement models for any or all of the variables. The research team is composed of Drs. Ji Seung Yang (PI), Yang Liu (co-PI), and Peter Steiner (co-PI).
Semiparametric Factor Analysis for Item Responses and Response Time
(NSF SES-1826535)
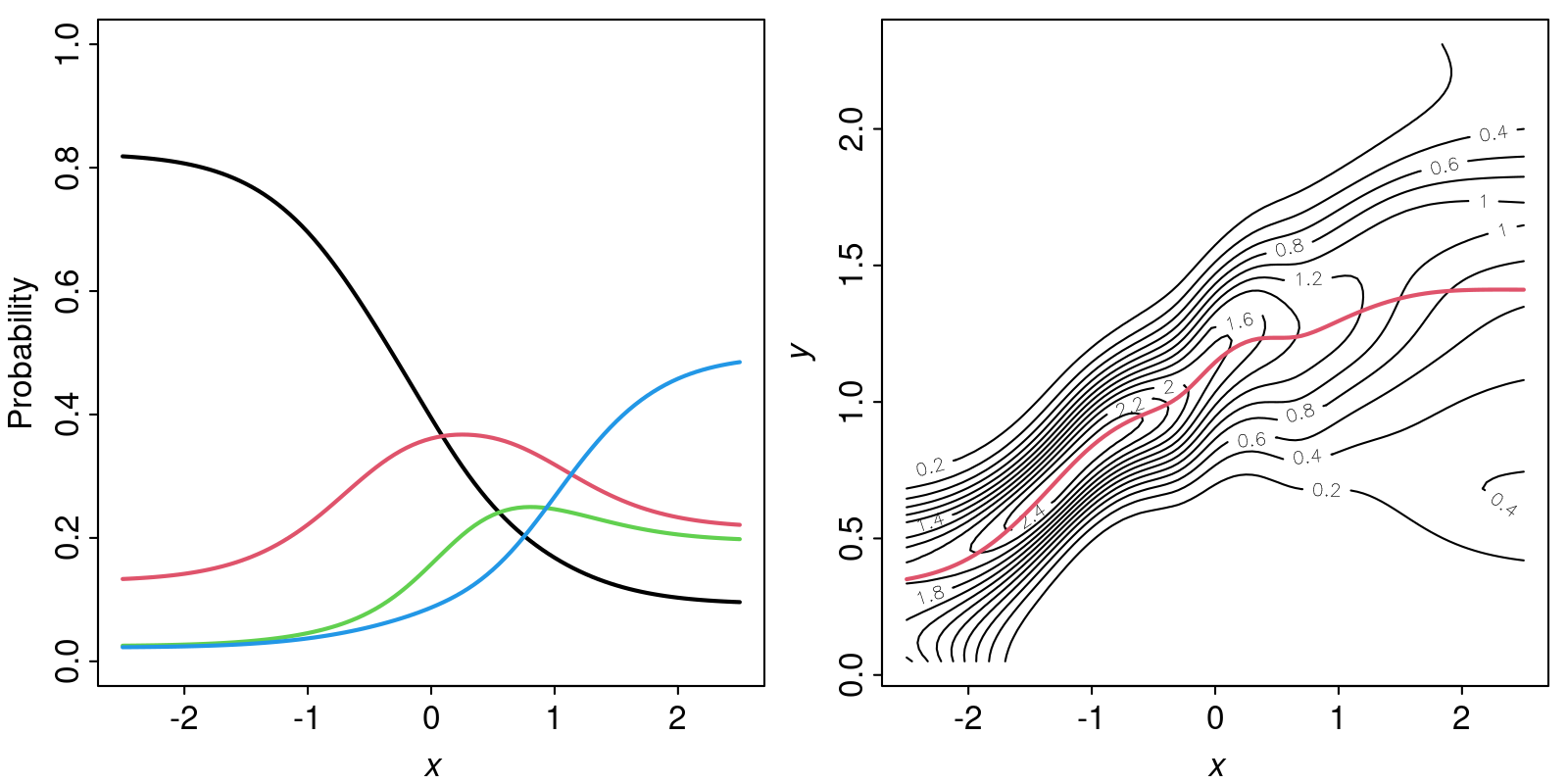
This research project develops a generic modeling framework for measuring latent traits, such as language proficiency and cognitive skills, from item response and response-time data. Response time has been identified as a useful indicator for test performance, and further research on the role of response time benefits the practice of test/survey development and administration. The novel measurement model proposed in this project relies on very few parametric assumptions: It characterizes the conditional distributions of response variables given the latent traits as smooth probability mass/density functions and further approximates them by cubic splines.
Goodness-of-Fit Diagnostics for Latent Variable Models
Goodness-of-fit (GOF) of measurement models, such as IRT and factor analysis, can be assessed in either a global or piecewise fashion—the former provides an overall impression of the model quality whereas the latter helps to determine how the fitted model can be improved. Most of the GOF diagnostics are based on residuals, whose reference distributions can be approximated by either asymptotic theory or Monte Carlo simulation. This has been one of my long-standing research interests; many of my publications along this line were collaborative work with Dr. Alberto Maydeu-Olivares.
