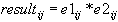 .
.





This chapter provides a more rigorous definition of MathViews' language structure. It provides details of data types, operators, statements, control flow structures, and file types.
Real Numbers Real numbers are integers and floating point numbers. Floating point numbers consist of an integer part, an optional decimal point, a fraction part, an "e" or "E," and an integer exponent. All floating point numbers are double precision. Some examples of real numbers are: 3.14159 and 10E-6
Complex Numbers Complex numbers are formed as follows: A number followed by "i" or "j" to represent a purely imaginary number. A number followed by "D" to represent a complex number in polar format with unit amplitude at the specified angle in degrees. A number followed by "R" to represent a complex number in polar format of unit amplitude at the specified angle in radians. Using one of the built-in functions, such as sqrt(-1), to create a complex number. The i and j constants above are defined in the script M-file startup.m. They are not built into the MathViews internal engine. However, D and R (also d and r) are built in. Some examples of complex numbers are: 2.5i or 3.4j 30D 0.55R 2+sqrt(-1)
Variable names are composed of letters and digits. The first character must be a letter. The underscore, "_", is recognized in MathViews as a letter. MathViews is case sensitive, by default, so upper and lower case characters are different. In addition, control-flow keywords like if, else, elseif, end, while, for, end, and break are reserved.
Variable names that start with the underscore are reserved. You should avoid naming variables with an underscore as the first character.
MathViews has two built-in variables, ans and eps. These two variables can be referenced or reassigned to new value. They cannot be cleared from memory. Issuing a "clear ans" command results in ans being set to [], the null matrix. Similarly, issuing a "clear eps" command results in eps being reassigned to 0.
The ans variable is used as the default variable to store the result of an expression if no other variable is specified as the result of the assignment.
The eps variable is used as the system's floating point tolerance. It has a default value of 0.
MathViews does not provide any additional built-in constants. You can simulate built-in constants by declaring them in the 'startup.m' script M-file. MathViews executes the 'startup.m' script file on powerup. The variable pi, for example, can be assigned pi = acos(-1) in the startup script M-file. This makes the variable pi available throughout a MathViews session.
Another method of setting the pi variable is to write a script M-file called pi.m. This M-file could contain the assignment pi = acos(-1). This M-file can be called from either the 'startup.m' or as an interactive command.
A string is a constant consisting of a series of ASCII characters enclosed in single quotation marks. The quotes are not part of the string.
Some examples of string variables are:
t = 'MathViews'
A = [ 'Here is a string';
'A:file1.m ';
'c:\user\file.txt ']
The basic unit of analysis in MathViews is a rectangular matrix. Scalars are 1-by-1 matrices and vectors are matrices with one row or column. The simplest way to enter a matrix is to enter an explicit list of elements. For example, to define a 2-by-3 matrix, enter:
A=[1 2 3;5 6 7]
The individual elements are separated by a comma or a space, and rows are separated by semicolons. Each element can be any MathViews expression, including other matrices. This allows complex matrices to be build up rather easily.
An expression is any series of symbols that MathViews uses to produce a value. The simplest expressions are constants and variable names that have no operator and generate a value directly. Operators combine expressions and values to produce new values.
MathViews operators fall into the following categories:
Unary operators: operate on a single operand.
Binary operators: combine two operands to perform a variety of arithmetic operations.
Assignment operators: assign a value to a variable, and optionally perform an additional operation before the assignment takes place.
The following table shows the set of MathViews operators arranged by precedence. Operators with highest precedence appear at the top of the table, and those with the lowest precedence appear at the bottom. Operators having the same precedence appear in the same row.
Precedence and Associativity of MathViews Operators
| |||
| Operator
|
Associativity
|
Type
| |
| Matrix
power
Array power
|
^
.^
|
left
to right
|
Binary
|
| Pre
and post increment
Pre and post decrement
|
++
--
|
left
to right
|
Unary
|
| Transpose
Conjugate Transpose
|
`
.'
|
left
|
Unary
|
| Matrix
multiplication Array multiplication Matrix division Array division Matrix division
Array division
|
* .* / ./ \
.\
|
left
to right
right to left
right to left
|
Binary
|
| Addition
Subtraction
|
+
-
|
left
to right
|
Binary
|
| Greater
than Greater or equal Less than Less or equal Equal (logical)
Not equal
|
~=
|
left
to right
|
Binary
|
| And Or
Not
|
& |
~
|
left
to right
|
Binary
Unary
|
| Rotate
Shift
|
<>
>>
|
left
to right
|
Binary
|
| Pipe
|
->
|
left
to right
|
Binary
|
| Colon
|
:
|
||
| Assignments
|
= += -= *= /=
:=
|
left
to right
right to left
|
Parentheses are used to change the associativity of MathViews operators. Parentheses can be nested arbitrarily deep. An example of a parenthesized expression is:
(1+4*(5+2))*3+10
(A & B) | C | ( ~ A)
(sqrt(2) + A)
MathViews provides facilities for block-structured conditional control-flow statements. Several statement formats are included in MathViews to perform loops, to select other statements to be executed, and to transfer control. The list of the reserved keywords is:
if, elseif, else, for, while, break, return, end
Syntax: -e1
If e1 is a scalar: The result is a scalar and is the arithmetic negation of e1.
If e1 is a matrix: The negation operates on every element of e1, and the result is a matrix with the same dimensions as e1.
The negation operator is defined for real and complex expressions.
Syntax: e1 + e2
If e1 and e2 are scalars, then the standard addition is performed.
If e1 is a scalar and e2 is a matrix, then e1 is added to every element of e2. The result is a matrix with the same dimensions as e2. Similar operations are taken if the types of e1 and e2 are reversed.
If e1 and e2 are matrices, then addition of matrices is performed on an element-by-element basis. The result is a matrix with the same dimensions as e1 and e2. Matrix addition is defined only for matrices with the same dimensions.
The addition operator is defined for real and complex expressions.
Syntax: e1 - e2
The subtraction operator adds to e1 the arithmetic negation of e2, i.e. e1-e2=e1+(-e2). All the rules of addition apply to subtraction.
Syntax: e1 * e2
If e1 and e2 are scalars, then the standard multiplication is performed.
If e1 is a scalar and e2 is a matrix, then every element of e2 is multiplied by e1. The result is a matrix with the same dimensions as e2. Similar operations are taken if the types of e1 and e2 are reversed.
If e1 and e2 are matrices, then the multiplication is only defined when the number of columns of e1 is the same as the number of rows of e2. The standard matrix multiplication is performed. This yields a matrix whose numbers of rows correspond to the number of rows of e1 and whose number of columns corresponds to the number of columns of e2.
The matrix multiplication operator is defined for real and complex expressions.
Syntax: e1 / e2 (right division)
If e1 and e2 are scalars, then standard division is performed, (e1 divided by e2).
If e1 is a scalar and e2 is a matrix, then every element of e2 is set to e1 times the reciprocal of the element of e2. The result is a matrix with the same dimensions as e2.
If e1 is a matrix and e2 is a scalar, then every element of e1 is divided by e2. The result is a matrix with the same dimensions as e1.
If e1 and e2 are matrices, then, if the inverse of e2 exists, the result is e1*inv(e2). The rules of matrix multiplication then apply to e1*inv(e2).
It is an error to divide by 0.
The matrix division operator is defined for real and complex expressions.
Syntax: e1 \ e2 (left division)
If e1 and e2 are scalars, then standard division is performed, i.e. e2 divided by e1.
If e1 is a scalar and e2 is a matrix, then every element of e2 is divided by e1. The result is a matrix with the same dimensions as e2.
If e1 is a matrix and e2 is a scalar, then every element of e1 is set to e2 times the reciprocal of the elements of e1. The result is a matrix with the same dimensions as e1.
If e1 and e2 are matrices, then, if the inverse of e1 exists, the result is inv(e1)*(e2). The rules of matrix multiplication then apply to inv(e1)*e2.
It is an error to divide by 0.
The matrix division operator is defined for real and complex expressions.
Syntax: e1 .* e2
If e1 and e2 are scalars, then the operation is the same as e1*e2.
If e1 is a scalar and e2 is a matrix, then the operation is the same as e1*e2.
If e1 and e2 are matrices, an element-by-element multiplication of e1 and e2 is performed. The result is a matrix with dimensions of e1 and e2 following the rule:
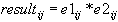 .
.
The dimensions of matrices e1 and e2 must be equal.
The array multiplication operator is defined for real and complex expressions.
Syntax: e1 ./ e2 (right array division)
If e1 and e2 are scalars, then the operation is the same as e1/e2.
If e1 is a scalar and e2 is a matrix, then the operation is the same as e1/e2.
If e1 is a matrix and e2 is a scalar, then the operation is the same as e1/e2.
If e1 and e2 are matrices, then an element by element division of e1 by e2 is performed, independent of the existence of the inverse of e2. The result is a matrix with dimensions of e1 and e2 following the rule:
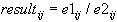 .
.
The dimensions of e1 and e2 must be equal.
It is an error to divide by 0. Right and left divisions are the same, except that the roles of the numerator and the denominator are switched.
The array division operator is defined for real and complex expressions.
Syntax: e1 .\ e2 (right array division)
If e1 and e2 are scalars, then the operation is the same as e1\e2.
If e1 is a scalar and e2 is a matrix, then the operation is the same as e1\e2.
If e1 is a matrix and e2 is a scalar, then the operation is the same as e1\e2.
If e1 and e2 are matrices, then an element by element division of e2 by e1 is performed, independent of the existence of the inverse of e1. The result is a matrix with dimensions of e1 and e2 following the rule:
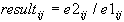 .
.
The dimensions of e1 and e2 must be equal.
It is an error to divide by 0. Right and left divisions are similar, except that the roles of the numerator and the denominator are switched.
The array division operator is defined for real and complex expressions.
Syntax: e1 ^ e2
If e1 and e2 are scalars, then e1 is raised to the e2 power.
If e1 is a matrix and e2 is a scalar, then e1 is multiplied by itself e2 number of times, following the rules of matrix multiplication. The result is a matrix with the same dimensions as e1. However, reversing the roles of e1 and e2 is an error.
If e1 and e2 are both matrices, the operation is undefined and causes an error.
The matrix exponentiation operator is defined for real and complex expressions.
Syntax: e1 .^ e2
If e1 and e2 are scalars, then the operation is the same as e1 ^ e2.
If e1 is a matrix and e2 is a scalar, then the operation is the same as e1 ^ e2.
If e1 and e2 are matrices, then, element by element, each element of e1 is raised to the power of the corresponding element of e2, following the rule:
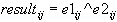 .
.
The dimensions of e1 and e2 must be equal.
The array exponentiation operator is defined for real and complex expressions.
MathViews provides a full set of relational and logical operators to support control flow statements. All the logical and relational operators are defined for real and complex numbers. However, when complex numbers are involved, only the real part of the complex number is used for operations. One exception is that the NOT operator does not support complex numbers.
The logical and relational operators yield a 0 if the specified relation is false and a 1 if the relation is true. Care must be exercised when comparing floating point numbers.
Syntax: e1 > e2
If e1 and e2 are scalars, then the result is a 1 if e1 is greater than e2; otherwise the result is a 0.
If e1 is a scalar and e2 is a matrix, then the comparison will operate on every element of e2 against the scalar e1, yielding a 1 if e1 is greater than the element of e2, otherwise yielding a 0. The result is a logical matrix with dimensions of e2. The same operation is performed if e1 and e2 exchange positions.
If e1 and e2 are matrices, then the dimensions of e1 and e2 must be equal. Every element of e1 is compared to the corresponding element of e2 following the rule:
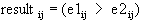 .
.
The result is a logical matrix with the same dimensions as e1 and e2.
Syntax: e1 >= e2
If e1 and e2 are scalars, then the result is a 1 if e1 is greater than or equal to e2; otherwise the result is a 0.
If e1 is a scalar and e2 is a matrix, then the comparison will operate on every element of e2 against the scalar e1, yielding a 1 if e1 is greater than or equal to the element of e2, otherwise yielding a 0. The result is a logical matrix with dimensions of e2. The same operation is performed if e1 and e2 exchange roles.
If e1 and e2 are matrices, the dimensions of e1 and e2 must be equal. Every element of e1 is compared with the corresponding element of e2 following the rule:
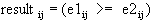 .
.
The result is a logical matrix with the same dimensions as e1 and e2.
Syntax: e1 < e2
If e1 and e2 are scalars, then the result is a 1 if e1 is less than e2; otherwise the result is a 0.
If e1 is a scalar and e2 is a matrix, then the comparison will operate on every element of e2 against the scalar e1, yielding a 1 if e1 is less than the element of e2, otherwise yielding a 0. The result is a logical matrix with the dimensions of e2. The same operation is performed if e1 and e2 exchange roles.
If e1 and e2 are matrices, the dimensions of e1 and e2 must be equal. Every element of e1 is compared with the corresponding element of e2 following the rule:
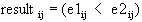 .
.
The result is a logical matrix with the same dimensions as e1 and e2.
Syntax: e1 <= e2
If e1 and e2 are scalars, then the result is a 1 if e1 is less than or equal to e2, otherwise the result is a 0.
If e1 is a scalar and e2 is a matrix, then the comparison will operate on every element of e2 against the scalar e1, yielding a 1 if e1 is less than or equal to the element of e2; otherwise it yields a 0. The result is a logical matrix with dimension of e2. The same operation is performed if e1 and e2 exchange roles.
If e1 and e2 are both matrices, the dimensions of e1 and e2 must be equal. Every element of e1 is compared with the corresponding element of e2 following the rule:
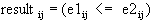 .
.
The result is a logical matrix with the same dimensions as e1 and e2.
Syntax: e1 == e2
If e1 and e2 are scalars, then the result is a 1 if e1 equals e2; otherwise the result is a 0.
If e1 is a scalar and e2 is a matrix, then the comparison will operate on every element of e2 against the scalar e1, yielding a 1 if e1 equals the element of e2; otherwise it yields a 0. The result is a logical matrix with the dimensions of e2. The same operation is performed if e1 and e2 exchange roles.
If e1 and e2 are both matrices, the dimensions of e1 and e2 must be equal. Every element of e1 is compared with the corresponding element of e2 following the rule:
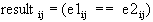 .
.
The result is a logical matrix with the same dimensions as e1 and e2.
Syntax: e1 ~= e2
If e1 and e2 are scalars, then the result is a 0 if e1 equals e2; otherwise the result is a 1.
If e1 is a scalar and e2 is a matrix, then the comparison will operate on every element of e2 against the scalar e1, yielding a 0 if e1 equals the element of e2, otherwise yielding a 1. The result is a logical matrix with dimension of e2. The same operation is performed if e1 and e2 exchange roles.
If e1 and e2 are matrices, the dimensions of e1 and e2 must be equal. Every element of e1 is compared with the corresponding element of e2 following the rule:
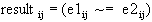 .
.
The result is a logical matrix with the same dimensions as e1 and e2.
Syntax: ~e1
If e1 is a scalar, then the result is a 1 if e1 is 0, and the result is 0 if e1 is non zero.
If e1 is a matrix, then the logical negation operates on each element individually, following the rule stated above.
The logical negation operator does not support complex numbers and complex matrices.
Syntax: e1 & e2
If e1 and e2 are scalars, then the result is a 1 if e1 and e2 are not 0; otherwise the result of the logical AND is a 0.
If e1 is a scalar and e2 is a matrix, then the logical AND operates on each element of e2 individually and logically compares them with the real value e1, following the rule stated above. The result is a logical matrix with the same dimensions as e2. The same operation is performed if e1 and e2 exchange positions.
If e1 and e2 are matrices, the dimensions of e1 and e2 must be equal. Every element of e1 is AND'd with the corresponding element of e2 following the rule:
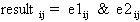 .
.
The result is a logical matrix with the same dimensions as e1 and e2.
The logical negation operator does not support complex numbers and complex matrices.
Syntax: e1 | e2
If e1 and e2 are scalars, then the result is a 0 if e1 and e2 both are 0; otherwise the result of the logical OR is a 1.
If e1 is a scalar and e2 is a matrix, then the logical OR operates on each element of e2 individually and logically compares them with the scalar value e1, following the rule stated above. The result is a logical matrix with the same dimensions as e2. The same operation is performed if the positions of e1 and e2 are exchanged.
If e1 and e2 are matrices, the dimensions of e1 and e2 must be equal. Every element of e1 is OR'd with the corresponding element of e2 following the rule:
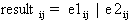 .
.
The result is a logical matrix with the same dimensions as e1 and e2.
The logical negation operator does not support complex numbers and complex matrices.
MathViews has several assignment operators, all of which group right-to-left. The left side of an assignment must be a variable and/or named sub matrix. Assignment operators will release any memory previously allocated to a variable before dynamically allocating memory for the new assignment.
Syntax: e1 = e2
The left side of the assignment operator, e1, must be a legitimate variable name, and the right side, e2, can be any legitimate MathViews expression or string. Any previous storage that had been allocated to e1 is released for future allocation, before the assignment takes place.
Syntax: e1(rV,cV) = e2
e1 is a named variable and must already exist prior to making the assignment.
e1(rV,cV) references a sub matrix in e1 that is replaced with e2, on an element by element basis. The sub matrix of e1 must have the same dimensions, i.e., equal number of elements, as e2. rV and cV are vectors specifying the rows and columns of e1 to be replaced by the elements of e2. Note that a scalar is a single-element vector.
Syntax: e1 += e2
The additive compound assignment syntax is a short hand notation for e1=e1+(e2).
Syntax: e1 = e2
The subtractive compound assignment syntax is a short-hand notation for e1=e1-(e2).
Syntax: e1 *= e2
The multiplicative compound assignment syntax is a short-hand notation for e1=e1*(e2).
Syntax: e1 /= e2
The division compound assignment syntax is a short-hand notation for e1=e1/(e2). However the \= compound assignment is not supported.
Syntax: ++e1; e1--; e1++; e1--MathViews implements the C operators for incrementing and decrementing variables. The increment operator(++) adds 1 to its operand while the decrement operator(--) subtracts 1 from its operand. These operators may be used either prefixed, as in ++x, or postfixed, as in x++, but the two cases have different meanings. The variable x is incremented in both cases, but in the expression ++x, x is incremented before its value is used, while x++ increments x after using its value. When x is an array, each element of the array will be incremented by 1. You should be aware of the different side-effects of these two operators.
For complex numbers, only the real part is incremented or decremented. There is no space between the variable name and the - or the ++ operators
Syntax: e1 := e2
This assignment makes variable e1 dependent on variable e2. If the value of e2 changes for any reason, e1 is automatically updated to reflect the new value of e2. However, if e1 is then reassigned, the old assignment is nullified.
You must be cautious when using the dependence operator. Circular relationships will trigger an error. For example, e1 := e2, e2 := e3; e3 := e1.
Matrix operators in MathViews permit you to manipulate matrix elements. Matrix operators operate on any type of matrix element, either complex or real.
Syntax: [e1; e2; ...]
The number of rows of the resulting matrix is the sum of the number of rows of e1 and e2 and any other matrices specified. The number of columns remains constant.
The number of columns in all of the matrices, e1, e2, ..., must be equal for vertical concatenation.
Syntax: [e1,e2, ...]
The number of columns of the resulting matrix is the sum of the number of columns of e1 and e2 and any other matrices specified. The number of rows remains constant.
The number of rows in all of the matrices, e1, e2, ..., must be equal for horizontal concatenation.
Syntax: e1 >> e2
Matrix rows and columns can be shifted in any direction, up, down, left, or right. The operand e2 can be a real scalar or a 2-element real vector. 0's are padded in when the rows/columns are shifted out.
If e2 is scalar, then e1 is shifted row-wise. If e2 > 0, e1 is shifted up, and if e2 < 0, e1 is shifted down. If e2 = 0, e1 remains the same.
If e2 is a vector, then the first element of e2 specifies the number of rows to be shifted, and the second element specifies the number of columns to be shifted. A positive element shifts left or up; a negative element shifts right or down.
If e2 is a matrix or a vector of more than 2 elements, MathViews will only use the first two elements of the vector or the first two elements of the first column of the matrix.
Linear shifting is not bit shifting. The operation affects only whole elements of rows/columns of a matrix.
Syntax: e1 <> e2
Matrix rows and columns can be circularly shifted in any direction, up, down, left, or right. The operand e2 can be a real scalar or a 2-element real vector.If e2 is a scalar, then e1 is shifted row-wise. If e2 > 0, e1 is circularly shifted up, and if e2 < 0, e1 is circularly shifted down. If e2 = 0, e1 remains the same.
If e2 is a vector, then the first element of e2 specifies the number of rows to be circularly shifted and the second element specifies the number of columns to be shifted. A positive element circularly shifts left or up, and a negative element circularly shifts right or down.
If e2 is a matrix or a vector of more than 2 elements, MathViews will only use the first two elements of the vector or the first two elements of the first column of the matrix.
Circular shifting is not circular bit shifting. The operation affects only whole elements of rows/columns of a matrix.
Syntax: e1' This unary operator takes the argument to its left and performs a conjugate transpose of the elements of e1.
Syntax: e1.' This unary operator takes the argument to its left and transposes the elements in e1.
Syntax: e1:optional_expr: e2
This form of the colon operator will create a row vector, with the first element set to e1, and subsequent elements following the rule:

e1, e2, and the optional _expr must evaluate to real scalars. If the optional_expr is not provided as in e1:e2, then optional_expr is assumed to be 1. If an undefined range is specified, as in 1:-1:5 then an empty matrix is returned.
If e1, e2, or optional_expr are complex, only the real part is used in MathViews calculations.
Syntax: expr -> function
MathViews provides a simple notation for a sequence of built-in function calls. The output of one function may be connected to the input of another function using the pipe operator. This notation is useful for replacing parentheses when the expression is deeply nested. It can also reduce the probability of syntax errors due to missing closing parentheses.
This syntax can only be used when the first function returns only one argument. For example:
5->sin->abs
ans =
0.9589
Syntax: expr ...
The continuation operator,"...", is used to continue from one line of text to another without breaking the flow of input. When processing the command or statement internally, MathViews treats the continuation operator as a mark indicating that the next line after the ellipsis actually belongs to the current line.
Syntax: expr; When the semicolon operator appears after an expression, it is a message to the MathViews internal engine to suppress any output resulting from the expression.
Syntax: %comments A sequence of characters beginning with the percent operator (%) is treated as white space by the MathViews internal engine. A comment can contain any combination of characters up until the newline character. A newline character terminates the commenting sequence. Multiple comment lines must have the % operator at the beginning of each sequence of commenting text.
MathViews provides facilities for block-structured control flow that specifies the order in which computations are performed. The syntax and semantics of the MathViews control-flow facilities follow those of the MATLAB language.
Syntax:
if expression
if statements
elseif
elseif statements
else
else statements
end
The elseif and else parts are optional. The expression is first evaluated, and if it is true, i.e. expression has a non zero value, the if statements are executed. Otherwise, if expression is false, i.e. the expression yields a 0 value, and if there is an else part, the else statements are executed.
Syntax:
while expression
while statements
end
The expression is evaluated and if it is true, i.e. non zero, the while statements are executed. This is repeated as long as the expression is true. The loop continues until the expression becomes false, at which point the execution resumes after the while statement.
Syntax:
for loop_variable=expression
for statements
end
This loop is executed N times, where N is the number of columns of expression. The loop_variable takes the value of each column of the expression.
For example, if expression is 1:5, the loop is executed five times with the loop_variable taking on the scalar values from 1 to 5.
Syntax: [out1,out2,...,outM]=funcname(in1,in2,...,inN)function statements
A user-defined function resides in an external file whose name is the same as the function name and whose extension is .m. The file is referred to as an M-file. A function can have multiple arguments and may return multiple values. Input arguments are passed by value, and output arguments are pass by reference. Both arguments have local scope. There are two run-time variables, nargin and nargout, which contain the number of input and output arguments that the function was invoked with. Functions may be called recursively, but the function stack has limited depth. Functions can call any other functions in the same module or a different module. However, when calling other modules, the modules must be in MathViews' path. The square brackets can be omitted, but only if the function only returns one argument. It is best, as a standard practice, to include the square brackets at all times. Multiple functions can be grouped together in a module and compiled into a library using the MathViews library compilation utility.
Syntax: !appname Invoking other applications in Windows is provided by using the exclamation operator. It should not be confused with the NOT operator as in the C language. MathViews will continue executing your program scripts after invoking the application. Since Windows is a non preemptive multitasking environment MathViews is not suspended while the other application is running. You must exercise caution when using the ! operator inside a loop. MathViews will try to bring up the same application as many times as the loop limit extends.
MathViews recognizes a number of different file types. These files are discussed in this section.
Files with the '.m' extension are called M-files. There are two types of M-files: a script M-file and a function M-file. A script M-file contains multiple statements doing related tasks. A function M-file, on the other hand, contains exactly one function, whose function name must be the same as the filename. Within the function declaration block, multiple statements and variables can exist for the purpose of manipulating the input and the returned output. M-files are brought into the MathViews memory in two ways: when the M-file filename is sent to the interpreter and when a "compile m-filename" command is issued. Once the M-file is brought into memory, it stays there until the clear command is used to take it out of memory.
Files with the '.l' extension, called L-files, are MathViews library module files. Each module can contain multiple functions, unlike the restriction on M-files where only one function is allowed per file. L-files cannot be script files. L-files only contain functions.L-files are brought into memory as they are compiled. The MathViews _lcompile function is used to perform all the required manipulations on L-files.
Files with the '.dry' extension are diary files. Diary files are files created to store a session's input commands. A diary file is created when the diary command is issued followed by the filename. All inputs to the interpreter will be copied to the diary file. To terminate a diary session, the "diary off" command must be issued.The default diary filename is 'mathview' if the filename is not specified when using the diary command.
Files with the '.mat' extension are storage files in MathViews. A storage file is generated when the save command is issued followed by the filename to be saved to. Storage files store a session's variables. Storage files are used in conjunction with the "load" and "save" commands. MathViews recognizes MATLAB '.mat' storage files.
Files with the '.mlb' extension are manipulated by the _loadlib and _savelib commands. MathViews will save the functions currently in memory into a file called 'mathview.mlb'. The _loadlib command will load the library functions in the file 'mathview.mlb'.
Files with the '.wmf' extension are graphics files in Windows graphics metafile format. Files with this extension can be manipulated using the meta and play command.
In MathViews, the search path is stored in the variable _MVPATH.
This variable must be updated every time the user adds a new MathViews-recognizable file type into the search path. The update is done in two ways:
1. Use the path option in the menu.
2. Use the following statement: _MVPATH = _MVPATH.
MathViews stores a look-up table in memory for all recognizable files in the search path. This allows faster access. Updating the _MVPATH variable causes the internal look-up table to be refreshed.
MathViews variables and constants are case sensitive. However, MathViews functions and commands are not case sensitive.
MathViews trigonometric arguments must be entered in radians. Trigonometric functions return values in radians.




