Collisional transport
Predicting flows of particles, heat, and electric current in magnetized plasmas
In magnetized plasmas, charged particles have complicated trajectories, drifting across the magnetic field lines due to nonuniformity in B (figure 2 here) . Particles also experience collisions, causing them to change from one trajectory to another. At the same time, sources and sinks of particles and heat mean that there are gradients of density and temperature. The interplay of geometrically complicated trajectories with collisions and density/temperature gradients gives rise to complicated non-Maxwellian distribution functions, as shown in figure 1. These phenomena result in flows of particles and heat, with two important consequences. First, these flows set the minimum possible rate at which heat leaks out of the confinement region; any turbulence would result in even higher energy loss. Second, differences between ion and electron flows represent an electric current, and this self-generated current in the plasma modifies the magnetic field. Together, these phenomena are called “collisional transport” or “neoclassical transport.”
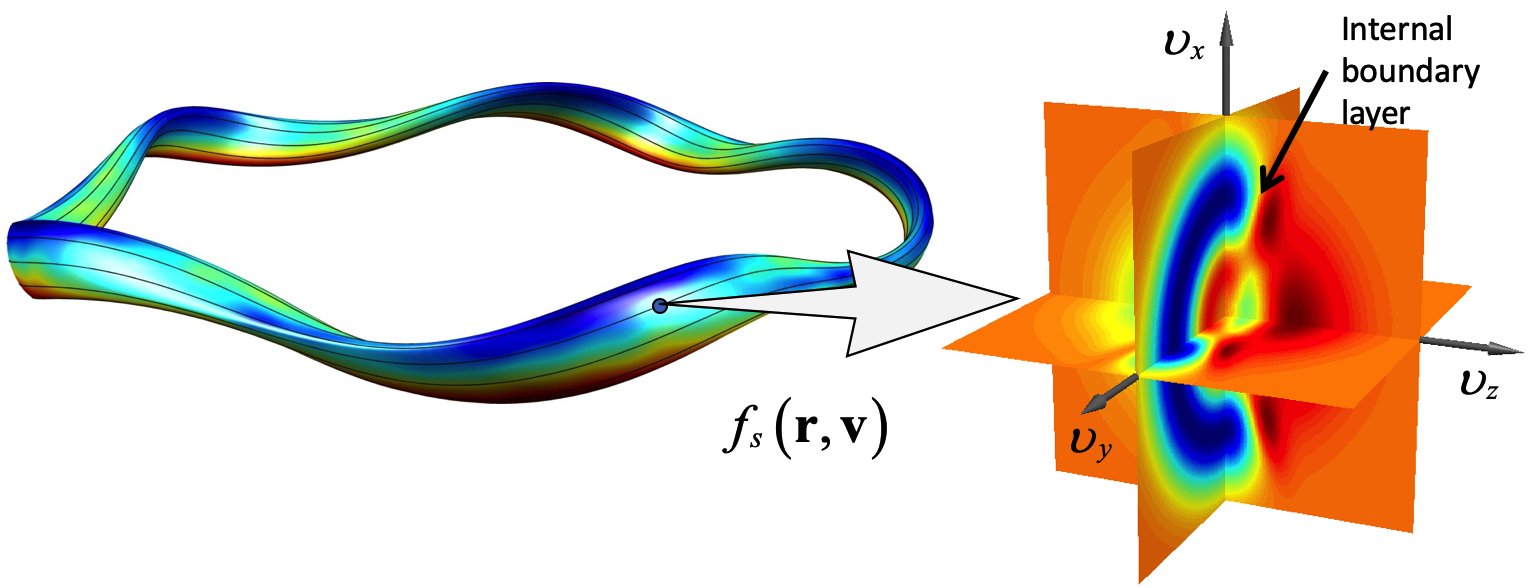
Computing these neoclassical effects is numerically challenging. One reason is the high dimensionality of the problem: not only real space but also velocity space must be discretized. Furthermore, high resolution in velocity space is required, since internal boundary layers in the distribution form at the boundaries between different classes of trajectories, as shown in figure 1. To solve this challenging problem, our group has developed the SFINCS code. SFINCS uses sophisticated numerical solver libraries to compute the distribution function in stellarator and tokamak plasmas. The code also computes moments of the distribution function to find the fluxes of particles and heat, and the self-generated electric current in the plasma.
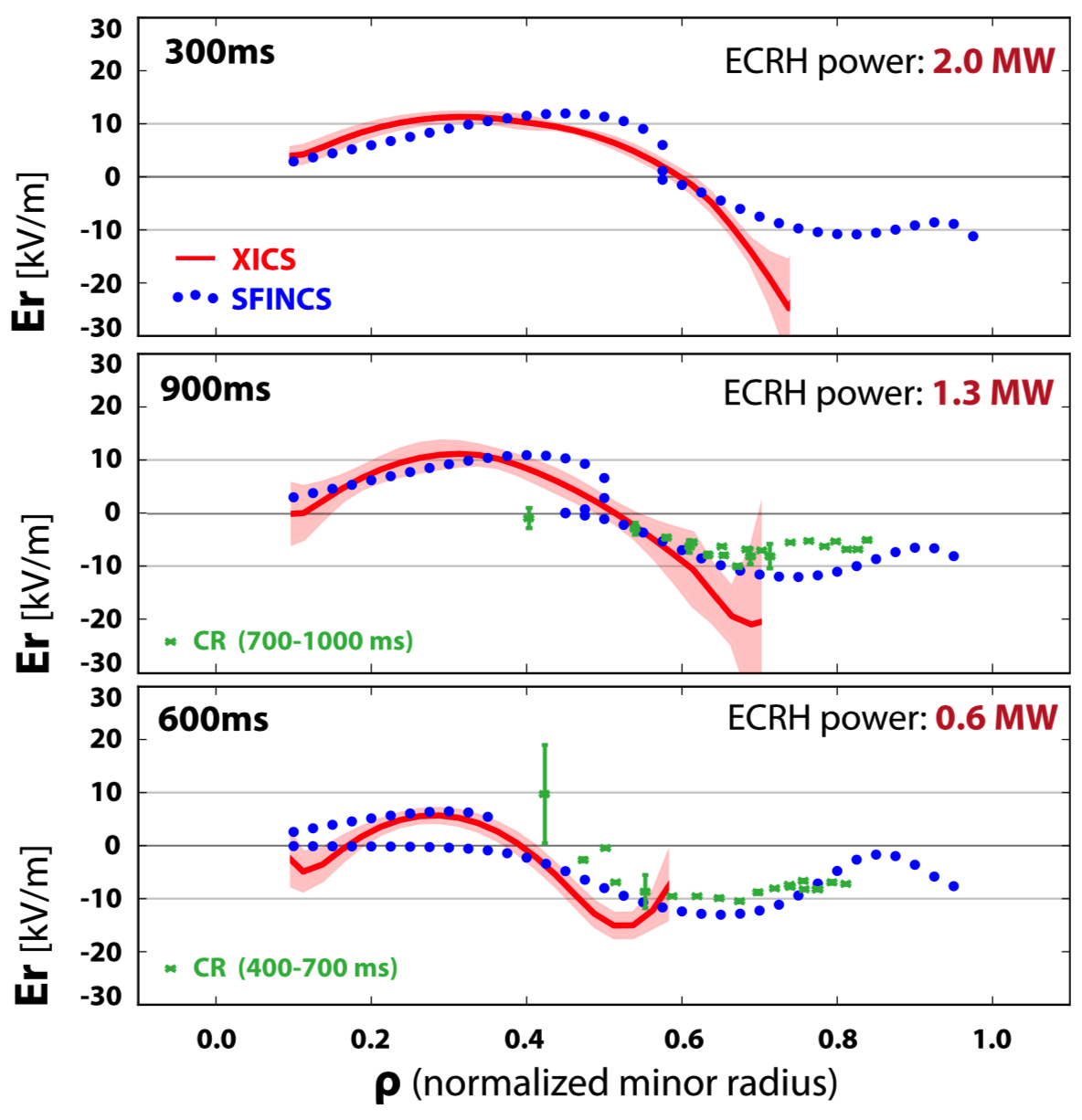
SFINCS is being applied to several stellarator experiments, including W7-X. Some papers describing SFINCS simulations of W7-X can be found here, here, and here. One example of experimental validation using SFINCS is shown in figure 2, which shows good agreement between the electric field computed by the code and the electric field measured in W7-X. SFINCS is also used at several companies, universities, and laboratories to predict the self-generated plasma current (“bootstrap current”) in future stellarator experiments.
At the same time, our group is also developing new numerical algorithms to make these calculations faster and less memory-intensive, so they can be used at greater scale in transport modeling and optimization. This work, led by postdoc Rory Conlin, exploits multigrid iterative methods. This next-generation neoclassical solver is under development in the new open-source package YANCC (Yet Another NeoClassical Code).