Wigner's Little Groups
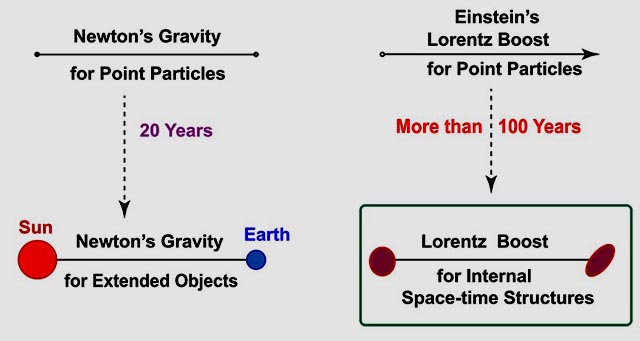
- We all know what Newton did. However, did you know that
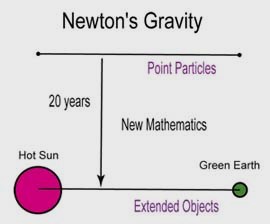
that, after he formulated his gravity law for point particles,
it took him 20 years to extend his law to extended particles.
In order to deal with this problem, Newton had to develop a new
mathematical instrument. You all know what this instrument is.
- In 1905, Einstein completed his special relativity. He formulated
the Lawrentz-transformation law for the space and time variables. He
also formulated the same law for the momentum and energy variables,
leading to his E = mc2 .
What happens when the particle has internal space-time structures ?

|
In order to deal with this problem, Newton had to develop a new mathematical instrument. You all know what this instrument is.
- Bohr and Einstein met occasionally to discuss physics. Einstein was interested
in how things appear to moving observers. Bohr was interested in the electron
orbit of the hydrogen atom. Did they ever talk about how the electron orbit
looks to moving observers? This is still the most outstanding problem in
physics.
The issue is then whether we have to invent a new mathematics or we can find suitable mathematical devices from the existing literature in mathematics. Indeed, in 1939, Eugene Wigner formulated the concept of the little groups which dictate the internal space-time symmetries of the particles in the Lorentz covariant world, as illustrated in this figure.

This aspect of Wigner's work is yet to be recognized. -
In 1939,
Wigner constructed subgroups of the Lorentz group whose
transformations leave the momentum of a given particle invariant. These
subgroups are called "Wigner's little groups."
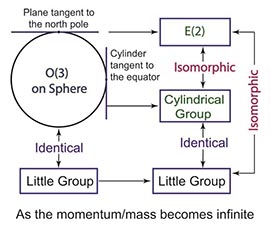
- If the particle is massive, there is a Lorentz frame in which
the particle is at rest. In this frame, the momentum is invariant
under three-dimensional rotations. Thus, the little group is O(3) or
the three-dimensional rotation group. This indeed tells the spin
degree of freedom. This aspect is so well known that Wigner's
little group is seldom mentioned.
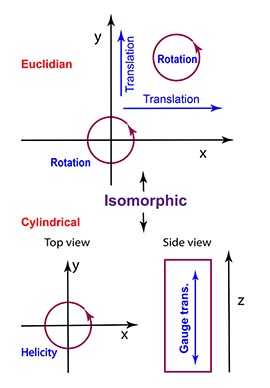
- In 1939, Wigner observed that the little group for massless
particles is isomorphic to E(2) or two-dimensional Euclidean group
with one rotational and two translational degrees of freedom. It
is easy to associate the rotational degree with the helicity of
the massless particle. What physics is associated with the
translations. This question was not completely settled until
1987. These two translational degrees of freedom collapse into
one gauge degree of freedom.
Click here for details.
- Einstein's the energy-momentum relation for the massive particle becomes the same as that for massless particle when its momentum is much larger than the mass. Likewise the O(3)-like little group for massive particle becomes the E(2) like little group when the momentum of the particle is much larger than the particle mass. Click here for a published article.

To the Nobel banquet of 1963, Wigner went with his wife and daughter. He invited his former high-school classmate named Kornel Gabor. He came with his wife and three daughters. Here is my photo Wigner's daughter (Princeton 2002).
I also had a photo with two of Gabor's daughters (Stockholm 2010). - If the particle is massive, there is a Lorentz frame in which
the particle is at rest. In this frame, the momentum is invariant
under three-dimensional rotations. Thus, the little group is O(3) or
the three-dimensional rotation group. This indeed tells the spin
degree of freedom. This aspect is so well known that Wigner's
little group is seldom mentioned.
- In this 1939 paper, Wigner deals with the first issue concerning the massive
particle at rest. However, the second and third issues were not settled
in 1963 when he received the Nobel prize. There have been two divided
opinions on his 1939 paper.
- This paper is only a mathematical exercise having nothing to do
with physics. This was the overwhelming view in 2963.
This is the reason why the Nobel citation did not
mention this paper.
- Wigner deserved a Nobel prize for this paper alone because it deals with the fundamental symmetries of the nature, but younger people should do some work to connect his mathematics to the physical world. Click here for an article on this issue.
We can organize these results in the following Einstein/Wigner table.

Einstein's Genealogy Massive/Slow between Massless/Fast Energy
MomentumE=p2/2m Einstein's
E=(m2 + p2)1/2E=p Helicity
Spin, GaugeS3
S1 S2Winner's
Little GroupHelicity Gauge Trans. Click here for a photo. Build
YOUR OWN HOUSE!You are then invited to build your own house. How are you going to build your own house? With what? In order to build a house consistent with it neighborhood is to find a Lorentz-covariant entity which takes different forms for slow and fast particles.
See next page.
portrait by Bulent Atalay (1978)
- This paper is only a mathematical exercise having nothing to do
with physics. This was the overwhelming view in 2963.
This is the reason why the Nobel citation did not
mention this paper.