Dirac's Poem for Squeezed States and Entangled Oscillators
According to Karl Marx, the point is to change the world. From the ancient times, many people changed the world by writing poems. The Book of Psalms from the Old Testament makes us happy and give us inspirations.
- Feynman and Wheeler communicated with each other by drawing cartoons.
Indeed, we can express physical ideas very effectively in the form of
cartoons. Feynman diagrams are cartoons. We often present our research
results in the form of graphs and tables.
Click here. You would agree that cartoons are graphic poems.
Those graphic poems play important roles in physics.
We can take a graphic approach to combine quantum mechanics and relativity. Click here for a graphic poem along this direction.
- Is it possible to write poems using mathematical formulas? You all
know how to write four Maxwell's equations. You will agree that this
set of equations constitutes a poem, and you all know how this mathematical
poem changed the world. If you did not know,
click here for a story of how this wireless world was created.
- Paul A. M. Dirac has his own style of writing physics books
and articles. You have all have read Dirac's book entitled
The Principles of Quantum Mechanics.
You will agree that this book is a book of poems.
I bought the fourth edition of this book in 1958. In Secs. 55 and and 56 of this book, Dirac wrote a poem using permutations. Presumably, this poem was based on his earlier experience with the Fermi-Dirac statistics. By writing this poem, Dirac concluded that the permeation can be regarded as a dynamical variable. I have a webpage dedicated to this subject.
- Dirac used to say that beautiful formulas are more likely to produce
profound physics. He was talking about himself. He produced new
physics by writing mathematical poems. He wrote most of his
mathematical poems using four-by-four matrices and harmonic
oscillators.
His Dirac equation for electrons and positrons was a history-making mathematical poem he wrote. Here he uses four gamma matrices, behaving like four vectors. From these matrices, we can construct axial vector, tensor, and pseudoscalar quantities. If we transform them into the Majorana representation, they all become 15 linearly independent traceless matrices with imaginary elements.
Dirac also wrote many poems using harmonic oscillators in the step-up and step-down representation. In quantum mechanics, we start with the commutation relation between x and p variables. In the oscillator regime, we start with the operators
-
[step-up = x + ip] and [step-down = x - ip]
Thus, Dirac's poems start with the uncertainty relation. I can write a long story about this, and let me stop here.
If you are interested in Dirac's role in quantization of electromagnetic field, you may read a review article entitled
On Dirac's New Method of Quantization,
written by Wolfgang Pauli (1943). Since Pauli and Dirac were so important to each other, particularly in quantum statistics and quantization of fields, I would love to post Pauli's photo with Dirac, but I could not find one. Instead, I picked up Pauli's photo with another distinguished physicist named C. S. Wu. She is famous for performing the first parity violation experiment.
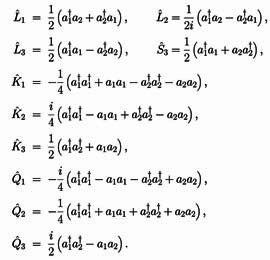
Dirac's poem on two entangled oscillators (above),
Dirac in 1962 while he was writing this poem.
- In his 1963 paper published in
J. Math. Phys. 4 , 901, Dirac considered two oscillators.
Again, he started writing a poem with step-up and step-down
operators. In so doing, he ended up with ten bilinear operators
stupefying a closed set of commutation relations.
Click here for their expressions.
- Dirac observed that these operators satisfy the set of
commutation relations for the O(3,2) deSitter group applicable to
the space consisting of three space-like and two time-like components.
- He also observed that it is also possible to construct a set
of generators for four-by-four matrices performing canonical transformations
for two sets of position and momentum variables.
-
Dirac did not mention whether this formalism can be applied to the
photon number states. However, we can forgive him in view of his
contribution to quantization procedure for electromagnetic field,
as
Pauli explained in his 1943 review paper.
- It is thus quite safe to say that Dirac wrote the first paper
leading to two-photon coherent states, or squeezed states.
- In addition, this set of operators leads to two harmonic
oscillators entangled to each other. What is so great about
engangled oscillators? The answer is very simple. Quantum
physics starts from two-level systems and harmonic oscillators.
In order to understand the mechanism of entanglement, it is
essential to work out the entangled oscillator system.

Photo of Dirac by Bulent Atalay. 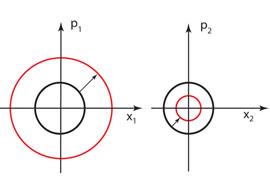
The phase spce to the first oscillator expands, and while that for
the second oscillator shrinks. - His ten oscillator-based generators can be converted to ten
four-by-four matrices applicable to four dimensional phase space
consisting two position and two momentum variables. They can also
be written as ten four-by-four matrices with imaginary elements.
Click here for detailed
computations to produce these matrices from Dirac's oscillator-based
generators.
Let ug go back to the Dirac equation. There are fifteen Dirac matrices in the Majorana representation. This set includes all ten matrices needed for squeezed states or entanglement. How about the remaining five matrices?
If we take them into account, the result is that the phase space for the first oscillator can expand like a thermal expansion, while the other shrinks without a lower limit. This result raises the following possibilities.
- The phase space expands for the first oscillator, while it
is shrinking for the second oscillator. If the second oscillator
is not observed, the first oscillator goes through a thermal
excitation. This point was discussed in terms of Feynman's
rest of the universe in my
recent paper
with Marilyn Noz.
- For the two-oscillator system, the uncertainty relation should be defined in terms of the four-dimensional phase space. The minimum uncertainty could be defined in terms of the minimum volume.
These questions could be debated in the future. Indeed, Dirac's matrix poems and oscillator poems lead to these intriguing questions.
- The phase space expands for the first oscillator, while it
is shrinking for the second oscillator. If the second oscillator
is not observed, the first oscillator goes through a thermal
excitation. This point was discussed in terms of Feynman's
rest of the universe in my
recent paper
with Marilyn Noz.

|
|
Elvis and Marilyn on the wall of
the Brasserie New York in Metz (France). I was there in 2012. |
However, we do not have to get that sophisticated to appreciate the power of poems in musical forms. When you sing your national anthem, you are reciting a poem both using its lyrics and its music. Yes, all songs are poems.
Elvis Presley was drafted to the U.S Army when I was an undergraduate student. He was so crazy that we all predicted that the Army would straighten him up. The net result was that Elvis changed the world. Perhaps he did not compose all those poems, but Elvis recited them well. In either case, poems are powerful, and they can change the world.

|
| from the Jadwin Hall of Princeton University. |
| |

|
|
James Clerk Maxwell (1831-1878). This photo is in the public domain. |
| |

|
| Click here to see where this portrait came from. |
Dirac met people, but he seldom communicated with them. Why?
- Dirac was Wigner's brother-in-law.
Click here for an interesting story. However, did they
communicate in physics. No, as far as I know. I used to
talk to Wigner in his late years, and I talked to Dirac twice.
In his 1949 paper, Dirac talks about a number of Wigner items contained in Wigne's 1939 paper on the Poincare group, but he does not make any reference to the Wigner's paper.
One of the communication difficulties could have been that Dirac knew how to use four-by-four matrices but could not use anything smaller. On the other hand, in order to communicate with Wigner, you had to use two-by-two matrices. I know this. I was talking to Wigner.
It was a rewarding experience for me to understand Dirac's four-by-four matrices in terms of the two-by-two matrices. Click here for one of the papers published along this line.

Yukawa and Dirac (Princeton 1953). - Dirac met Hideki Yukawa in 1953,
probably in New York. They met again in 1955. It appears that they
met in Kyoto (Japan) in 1955. I assume they talked about physics.
In 1953, Yukawa published a short paper entitled
Structure and Mass Spectrum of Elementary Particles. II. Oscillator Model
while he was visiting Columbia University.
In 1955, Yukawa became more intensely interested in harmonic oscillators,
while Dirac was using the oscillator language throughout his life.
However, there does not seem to be any published material to indicate that they talked about harmonic oscillators. With one of my co-workers, I was able to able to compose a paper on what they could talked to each other on the oscillator issue, and published the paper in the Progress of Theoretical Physics, the Japanese Physics Journal established by Hideki Yukawa.
In either case, both of them received their Nobel prizes for predicting new particles by writing mathematical poems.
Dirac, Yukawa, and their wives,
Kyoto (Japan 1955).It is my pleasure to post a photo of Dirac and Yukawa (Kyoto 1955). Their wives are also in the photo. I never met Professor Yukawa, but I once received a letter from Mrs. Yukawa. Click here for her handwritten letter. In this letter, she talks about Mrs. Margit Dirac. I met Mrs. Dirac in 1978 (in Florida) and in 1988 (in Princeton). I met Paul A. M. Dirac in 1962 and in 1978.
- Dirac met Feynman in 1962. Three months later, in October,
I met Dirac.
In the fall of 1962, I was a first-year assistant professor at the University of Maryland. I was his driver when Dirac came spent two weeks in Maryland. I was fortunate enough to sit down with him to talk about physics for about 30 minutes.
At that time, every physicist had to do follow order coming from Berkeley. I had to do "Regge poles" and "bootstraps." I did not like what they were doing, and I am the one who put an end to the bootstrapism in 1965. Click here for my story. This point was echoed by Geoffrey Chew who is known as the creator of bootstrap dynamics. Click here for Chew's paper.
Thus, when I met Dirac in 1962, I did not have any clear vision for myself. Indeed, it was Nicodemus meeting Jesus (Gospel of John). I asked Dirac what I should study. He said "American physicits" should spend more time to exploit contents of Lorentz covariance.
Jesus and Nicodemus, painting by
Crijn Hendricksz (1616–1645) (top). Dirac and Feynman met in Poland
(July 1962).
If I translate this into a carton, Dirac was saying this. Many years later, I was fortunate enough to add something to this cartoon, and produce this cartoon. A similar cartoon is contained in my recent paper recent paper Marilyn Noz.
However, the question was why Dirac was mentioning American physicists. This is an interesting question because Dirac seldom talked to American physicists.
- In Agust of 1963, the Physics Today carried
this photo of Dirac and Feynman on its cover page.
They mat at the International Conference on Relativistic Theories
of Gravitation in July of 1962 (three months before I met Dirac in
October), at the Jablonna Palace near Warsaw, Poland. I
suspected that Dirac was talking about Feynman when he mentioned
"American physicsits" to me. This photo clearly indicates there
was a communication gap between these two great physicists.
- In 1971, Feynman published this paper with his students. It then became clear to me that Dirac indeed was talking about Feynman, when he told me American physicists should study Lorentz covariance.
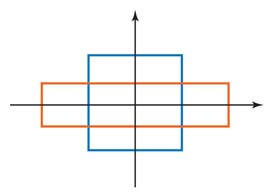
Two-by-two matrices can do this kind
of transformations. They can be
called "squeeze" transformations.
Click here for applications of these
two matrices in optical sciences.
- In Agust of 1963, the Physics Today carried
this photo of Dirac and Feynman on its cover page.
They mat at the International Conference on Relativistic Theories
of Gravitation in July of 1962 (three months before I met Dirac in
October), at the Jablonna Palace near Warsaw, Poland. I
suspected that Dirac was talking about Feynman when he mentioned
"American physicsits" to me. This photo clearly indicates there
was a communication gap between these two great physicists.
- This gave me enough motivation to build a research program:
to put Dirac and Feynman into one box. I talked about this issue
many times before, and I do not have to explain this again.
You can go back to my earlier page on
this subject.
In so doing, I found out why they could not talk to each other. Let us assume that they knew how to use two-by-two matrices for rotations. If they knew those matrices can also perform squeeze transformations, like this, or like this they could have communicated, and the physics world could have have been quite different. It is much easier to understand Dirac's papers and Feynman's papers in terms of those squeeze transformations.
- Without two-by-two rotation matrices, it would be very difficult
to do physics. Likewise two-by-two squeeze matrices are everywhere
in physics, including Dirac's mathematical poems (both based on
his gamma matrices and harmonic oscillators).
Feynman's 1971 paper
is messy because he did not know how to use those squeeze matrices.
You too may be using them in your papers too. The physics world could
be quite different if physicists know they are using these squeeze matrices.

- Let us finally talk about Nicodemus. I mention him often
during my conference talks. I talk about him when I mention
my encounter with Dirac in 1962. I then see blank faces
from the audience.
Nicodemus is mentioned in the Gospel of John, but he appears to be totally irrelevant to physics issues. Yet, I could be talking about you whenever I mention his name. In order to emphasize this point, let me tell you that I am not the first person who attempted to identify himself with Nicodemus.
- You all know Michelangelo was a creative person, and you would
not mind becoming as creative as he was, even though he was in
a different field. Among many of his sculptures, the most
famous one is
the Pieta
(Mary holding the body of Jesus taken down from the cross)
in Vatican's Saint Peter's Basilica.
There is another Pieta Michelangelo constructed in his later years. It is said that he constructed this Pieta to decorate his tomb in Rome, but it is now housed in in the Museo dell'Opera del Duomo in Florence.
- As you can see, Nicodemus is the most prominent figure in this sculpture. Here, Michelangelo portrayed himself as Nicodemus. Why did he do so? You may enjoy finding out the answer. The story could be talking about you.

|
| Two famous brothers-in-law. |

|
| How did he talk to Einstein? |
- His home page.
- His Dirac page.
- His Einstein page.
- His world travel page.
- The Wall Street Journal will publish this table.
