
PLEASE PRINT OUT THESE PAGES FIRST AND THEN KEEP THE PRINTED TEXT BESIDE YOU AS A GUIDE WHEN YOU LOAD AND RUN "NEURON". THIS WILL SAVE YOU HAVING TO JUGGLE BETWEEN NEURON AND NETSCAPE WINDOWS ONCE YOU HAVE THE SIMULATION LOADED.
To begin working with this chapter you should have downloaded and installed Neuron, as described in Chapter 1
First, you need to understand the real experimental situations that are being simulated by Neuron.
1. Electrophysiological recording set-up.
The Neuron programs that you will use simulate cells that are impaled
by glass micro-pipettes (micro-electrodes)
The micro-electrodes contain a highly conductive fluid (usually 3M KCl) and can be used either to measure membrane potential (voltage electrode) or to pass current into the neuron (current electrode).
The basic recording set-up therefore is a neuron impaled by two electrodes - a voltage electrode and a current electrode.
2. Modes of recording
There are two basic modes of recording the currents of whole neurons:
The two names refer to whether net membrane current or membrane potential (voltage) is to be controlled by the electronic apparatus connected to the micro-electrodes.
When you have read the definitions, below, of voltage clamp and current
clamp, proceed to Chapter 4.
Current clamp recording is closest to the situation that exists
under natural conditions.
To understand it, it is important to realize that under natural conditions
the net, total current across a neuronal membrane is zero. Ionic
currents may be flowing in through sodium channels and out through potassium
channels, but they balance, and the net current flowing is zero. Why? -
because there is no external source or sink of current, so that the circuit
of current flow has to be completed across the cell membrane - ionic currents
leaving the cell must be balanced by those returning.
Impaling a cell with a voltage micro-electrode does not disturb the
balance of currents since the electrode and attached amplifier ideally
draws no current from the cell and injects none into it.
We can therefore monitor the "natural" production of action and synaptic
potentials in response to synaptic input using a single voltage electrode.
However, being scientists, we want also to artificially stimulate neurons, so as to investigate how they respond to injected current. If we now impale a cell with a second current micro-electrode and pass current through it, we then impose a certain net current flow across the neuronal membrane. We have to be very careful about the amount of current we inject into the cell, so we monitor it and use a feedback circuit to "clamp" the injected current at a fixed value.
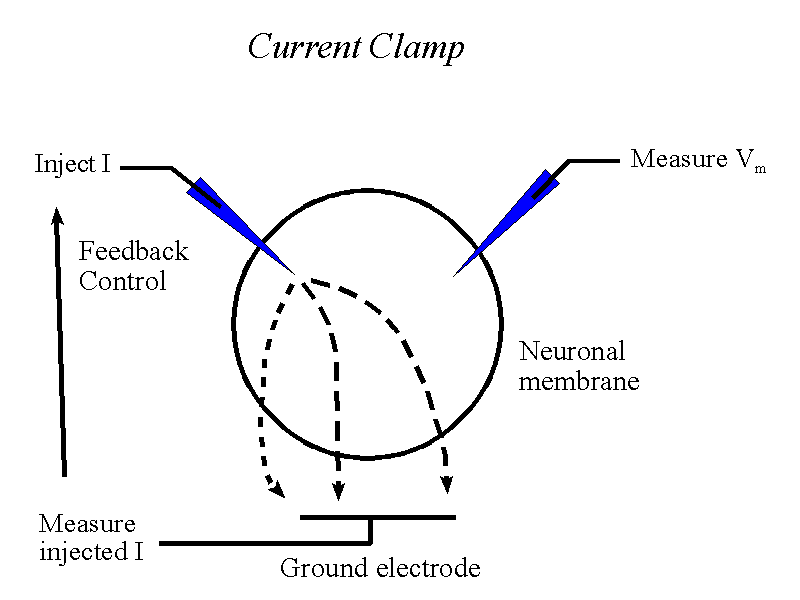
If we inject +ve current into the cell (by making the inside
of the current electrode positive) then the cell depolarizes.
If we inject -ve current into the cell (by making the inside
of the current electrode negative) then the cell hyperpolarizes.
It is important to realize that we have not clamped the membrane potential in this "current clamp" situation - membrane potential is free to vary - and that if the cell depolarizes enough in response to the injected current then action potentials will be generated and ionic currents will flow as usual through the voltage-dependent sodium and potassium channels
Thus current clamping cells can tell us about the response of cells to depolarization or hyperpolarization. The injection of current by the micro-elecrode mimics, to some degree, the currents flowing into the cell through post-synaptic channels.
Return to modes of recording
Voltage clamp recording is a trickier concept than current clamp.
In a voltage clamp situation, the membrane potential is measured by the
voltage electrode and is held constant by a feedback circuit that injects
current into the cell via the current electrode.

The important thing to realize is that the current that we inject into the cell has to pass through the neuron's membrane in order to complete its circuit to the ground connection. Thus the injected current is equal to the net current passing through all of the channels in the membrane. If we measure this current on its way to the ground connection, then we have a measure of the net, current, im , passing through the membrane channels at a particular clamped membrane potential.
But what is the reason for clamping the voltage at a particular value?
Well, you may recall from your texts the following equation: -
im = Cm(dVm/dt) + gNa(Vm-ENa) + gK(Vm-EK) +gleak(Vm-Eleak) - or put more simply
im = capacitive current + sum of ionic currents
(g = conductance; E = Nernst potential; Cm = membrane capacitance
)
Now when the membrane potential is voltage clamped at a constant value, then dVm/dt = 0 - capacitive current is zero - so that the measured total current is then equal to the sum of the ionic currents.
A voltage clamp circuit can therefore be used to measure the net current flowing through the ion channels at any given, fixed membrane potential.
But there is an added bonus:
Recall from your text that gNa and gK change with membrane potential as well as time. They are voltage-dependent conductances. Recall also that under normal (current clamp) conditions changes in gNa and gK lead to changes in Vm, resulting in the positive and negative feedback effects that create the action potential. With Vm fixed by the voltage clamp circuit, this complication is removed and the time-course of im reflects the much simpler time-course of the changes of the underlying conductances at a single fixed voltage. From the behavior of gNa and gK at a series of fixed voltages, models can be generated of the behavior of the conductances at all voltages and the way the conductances change with time and voltage. Model conductances of this kind, pioneered in 1952 by Hodgkin and Huxley, underlie most mathematical simulations of the action potential and provide great insight into the mechanism of channel gating. So......
A voltage clamp circuit can therefore be used to calculate
the conductance of ion channels that are active at any given, fixed membrane
potential.
Return to modes of recording