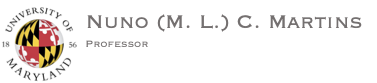Control-theoretic Methods for Incentive Design For Large Learning Agent Populations
This research focuses on the design of incentive mechanisms for large populations of learning agents using system theoretic passivity concepts that capture broad and realistic notions of rational behavior. The key idea is to shape learning outcomes through dynamic payoff incentives without requiring knowledge of the specific learning rules used by agents. As long as agents satisfy general passivity based rationality conditions the proposed incentives guarantee stability and convergence of the coupled system. Epidemic population games are used as a proof of concept where incentives represent policy interventions but the methods are not limited to public health applications. The same approach applies to energy markets congestion control and transportation systems where prices tolls or subsidies can be designed to guide decentralized learning toward socially desirable equilibria in a robust and scalable way.
System-Theoretic Passivity Methods for Nash Equilibrium Learning in Population Games
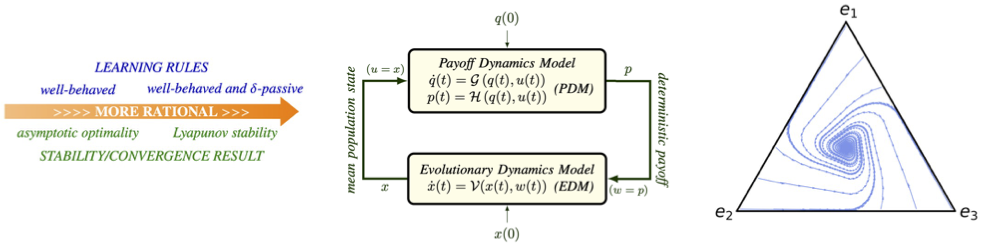
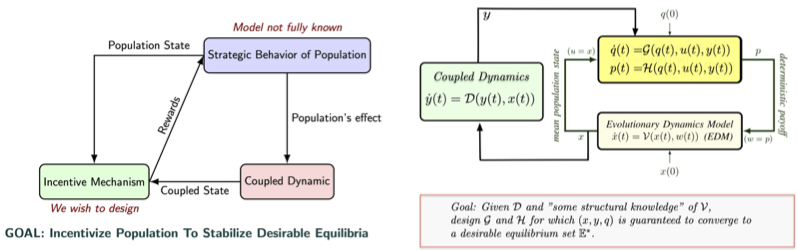
Professor Nuno C. Martins' research uses system-theoretic passivity methods to ensure stable learning dynamics in large population games involving strategic, non-cooperative interactions. By modeling the population's learning dynamics and payoff feedback as a closed-loop system, these frameworks guarantee convergence to Nash equilibria without requiring precise knowledge of individual learning rules. Martins and colleagues introduce new passivity notions (e.g., delta-passivity, equilibrium-independent passivity, and counterclockwise (CCW) dissipativity) that generalize classical input-output characterizations of rational behavior. This approach unifies earlier results (e.g., potential games) and expands stability guarantees to broader scenarios, including dynamic payoff processes and imitation-driven dynamics like replicator rules. Their passivity-based analysis provides robust convergence assurances for evolutionary Nash equilibrium learning across diverse population games.
Multidisciplinary Methods For Distributed Estimation
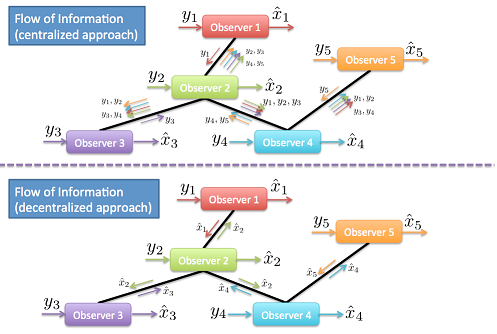
This work focuses on the design of algorithms to achieve omniscience of the dynamic variables of a group of mobile agents, subject to power and communication constraints. In collaboration with Greg Marshall from the National Geographic Society (Crittercam Group), we are developing a tracking platform that is fully programmable, supports wirelessly networked distributed algorithms, and features GPS, IMU and high definition camera recording capability. This work is sponsored by NSF and AFOSR.
Multidisciplinary Approaches to Fundamental Limits of Networked Control
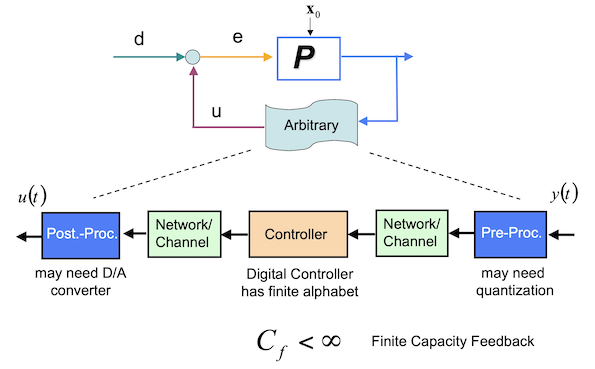
This research takes a multidisciplinary approach to feedback control, combining ideas from control theory, information theory, and communication systems. It reveals how uncertainty and finite-rate or noisy information channels fundamentally limit stabilization and disturbance rejection, and shows that information-theoretic principles impose unavoidable performance bounds even for nonlinear and time-varying control systems.
Multidisciplinary Methods For Distributed Control and Decision Systems
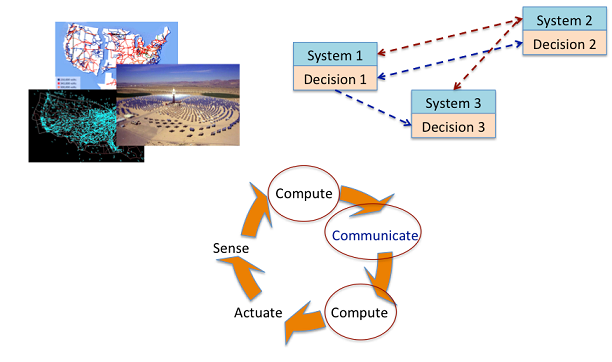
In collaboration with Serdar Yuksel (Queens U., Canada) and Aditya Mahajan (McGill U., Canada), we are investigating the structure and properties of optimal solutions to currently unsolved team decision problems. Some of our past work on optimal distributed estimation with communication costs, and optimal decentralized control subject to information constraints are also related to this topic. A tutorial on this topic was given at the 2012 IEEE Conference on Decision and Control, in collaborations with A. Mahajan, M. Rotkowitz and S. Yuksel. This work is supported by AFOSR and NSF.
Algorithms and Applications
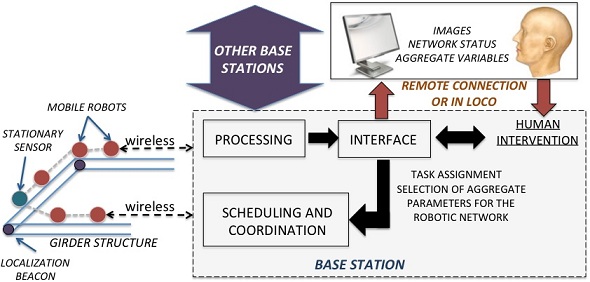
A related area of recent interest is the use of a formal team decision framework to investigate suitable information structures for mixed initiative team problems. This is specially relevant for networked robotic applications, where human and robots interact as a team. We have established a multidisciplinary discussion group on applications of these ideas for infrastructure safety inspection systems, with emphasis on bridges.
* We may provide drafts of unpublished work on these topics upon request