Optimization & shape derivatives | UMD Stellarator Group

A central concept in stellarator design is optimization. It is thought that neither integrabilty (i.e. good magnetic surfaces) nor quasisymmetry can be achieved perfectly in a field lacking true axisymmetry, so optimization is needed to minimize the departures from these two hidden symmetries. Numerical optimization has been central to the design of stellarators like W7-X and HSX, both to select the shape of the plasma and then to select the shape of the electromagnetic coils that generate the magnetic field. The design of a stellarator’s plasma shape and coil shapes is a problem that pushes the limits of optimization, for multiple reasons. Besides integrability and quasisymmetry, there are myriad other objectives such as minimizing plasma instabilities and minimizing the complexity of the coil shapes. The optimal design should be robust yet flexible, and it is not even clear what parameter space to optimize in. Evaluation of the objective functions requires numerous physics codes that must be efficient, since they are called thousands of times inside the optimization iteration. Our group is pursuing several problems in the area of optimization that will advance stellarator development.

Derivative-based formulations

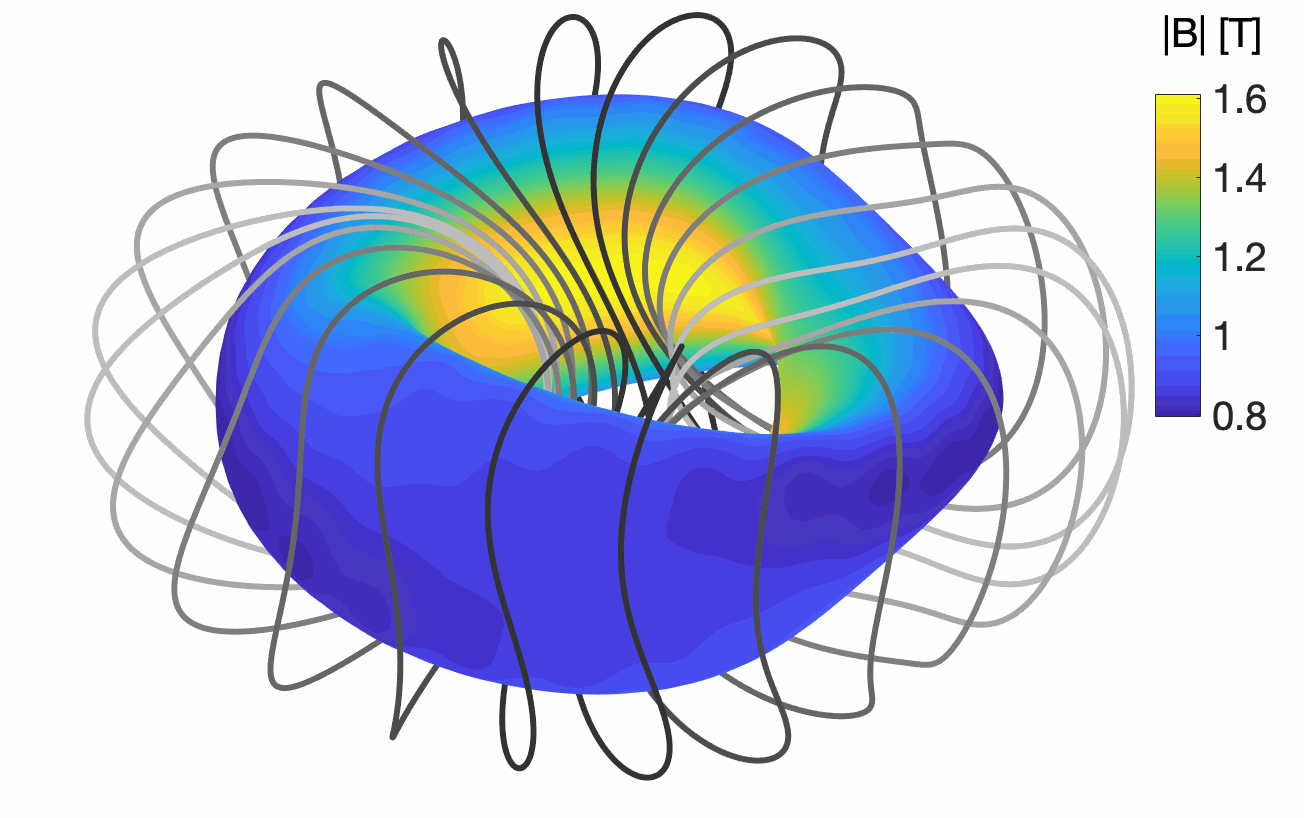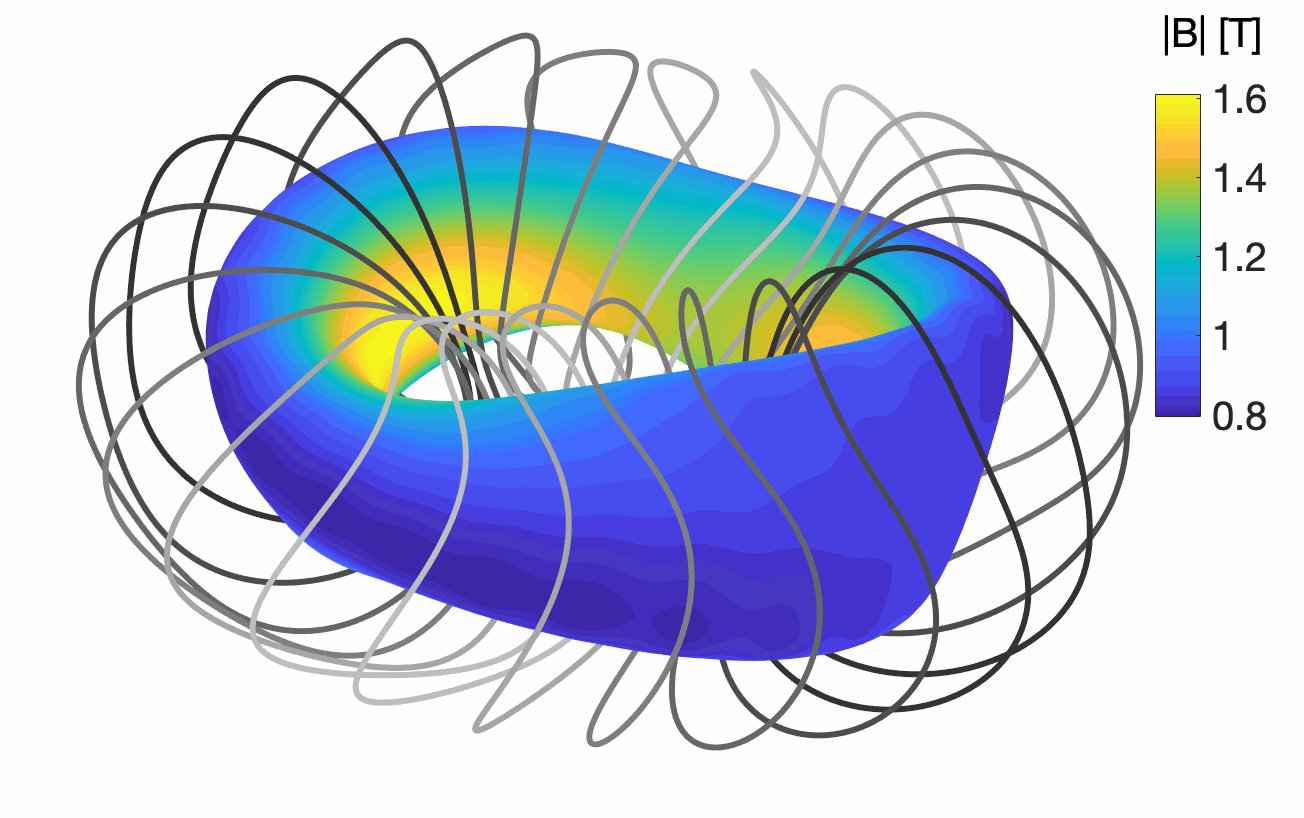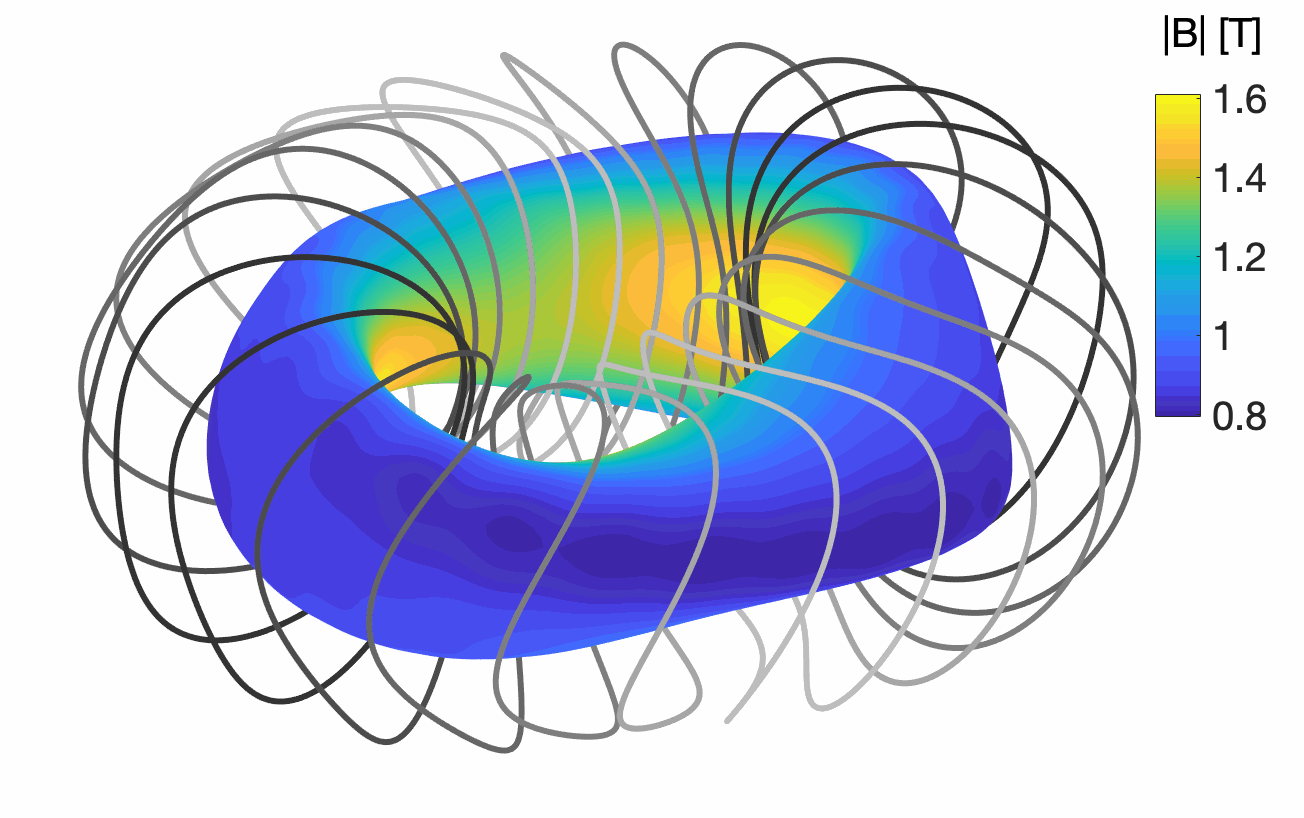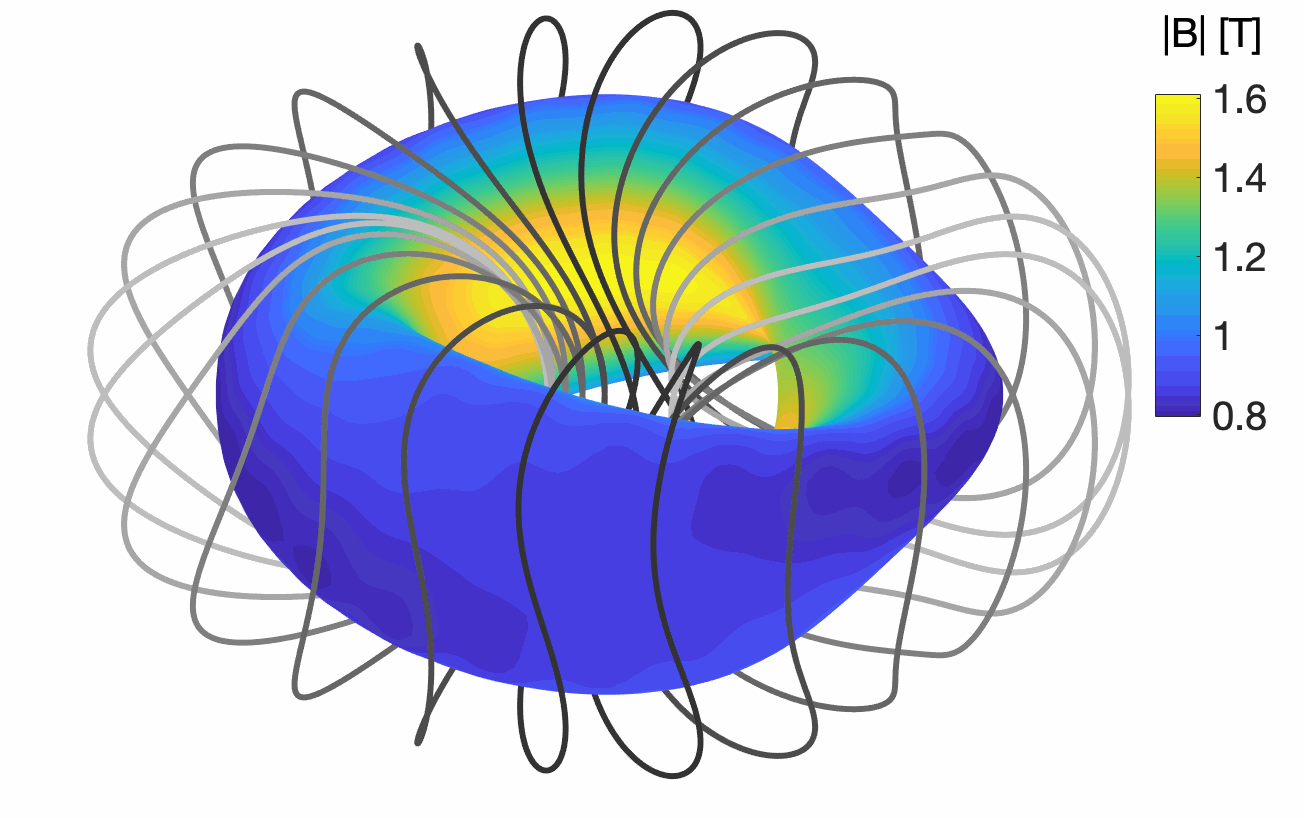
Optimization is greatly accelerated when derivatives are available. However, to date, stellarators have been designed using either derivative-free optimization or finite difference derivatives, which are expensive and introduce noice. Our group, working with collaborators at the NYU Courant Institute (Andrew Giuliani, George Stadler, Florian Wechsung), has been developing new formulations of the stellarator optimization problem in which analytic derivatives are available. This work involves reformulating the objective function to include quantities that are practical to differentiate. Figure 1 shows an example quasisymmetric stellarator for electron-positron confinement using one of our new derivative-based methods.

Figure 1. A quasisymmetric stellarator designed using the new gradient-based formulation.

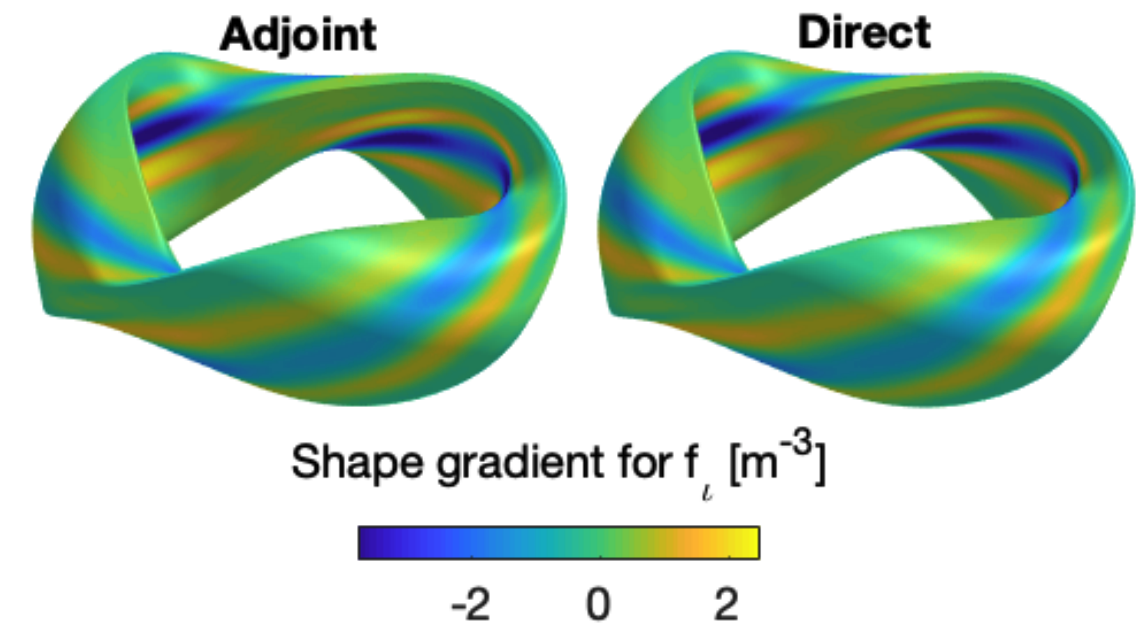
Adjoint methods and shape gradients

Adjoint methods are a powerful technique to compute derivatives at minimal computational expense. This derivative information can be applied both for derivative-based optimization and for sensitivity analysis. When applied to shape optimization, adjoint methods yield the shape gradient, which indicates how a figure of merit changes due to normal displacement of the boundary. While adjoint methods and shape gradients are widely used in other fields, such as aerospace and automobile design, they have hardly been used in plasma physics. Our group has pioneered the development of adjoint methods for stellarator problems, in papers by PhD student Elizabeth Paul (here, here, and here) and Professor Tom Antonsen (here). Figure 2 shows an example of a shape gradient computed for a stellarator using our adjoint methods.

Figure 1. The shape gradient for rotational transform in the NCSX stellarator, computed using an adjoint method by PhD student Elizabeth Paul. The right figure shows the same information can be obtained with finite-differencing, but at much higher computational cost than the adjoint method.