Plasma turbulence

Turbulence is ubiquitous in plasmas, just as it is in non-conducting gases and liquids. Plasma turbulence has features not found in other types of turbulence: velocity-space effects are often important, magnetic fields introduce strong anisotropy, and natural length scales like the gyroradius are significant. Our group studies several aspects of plasma turbulence.

Subcritical turbulence

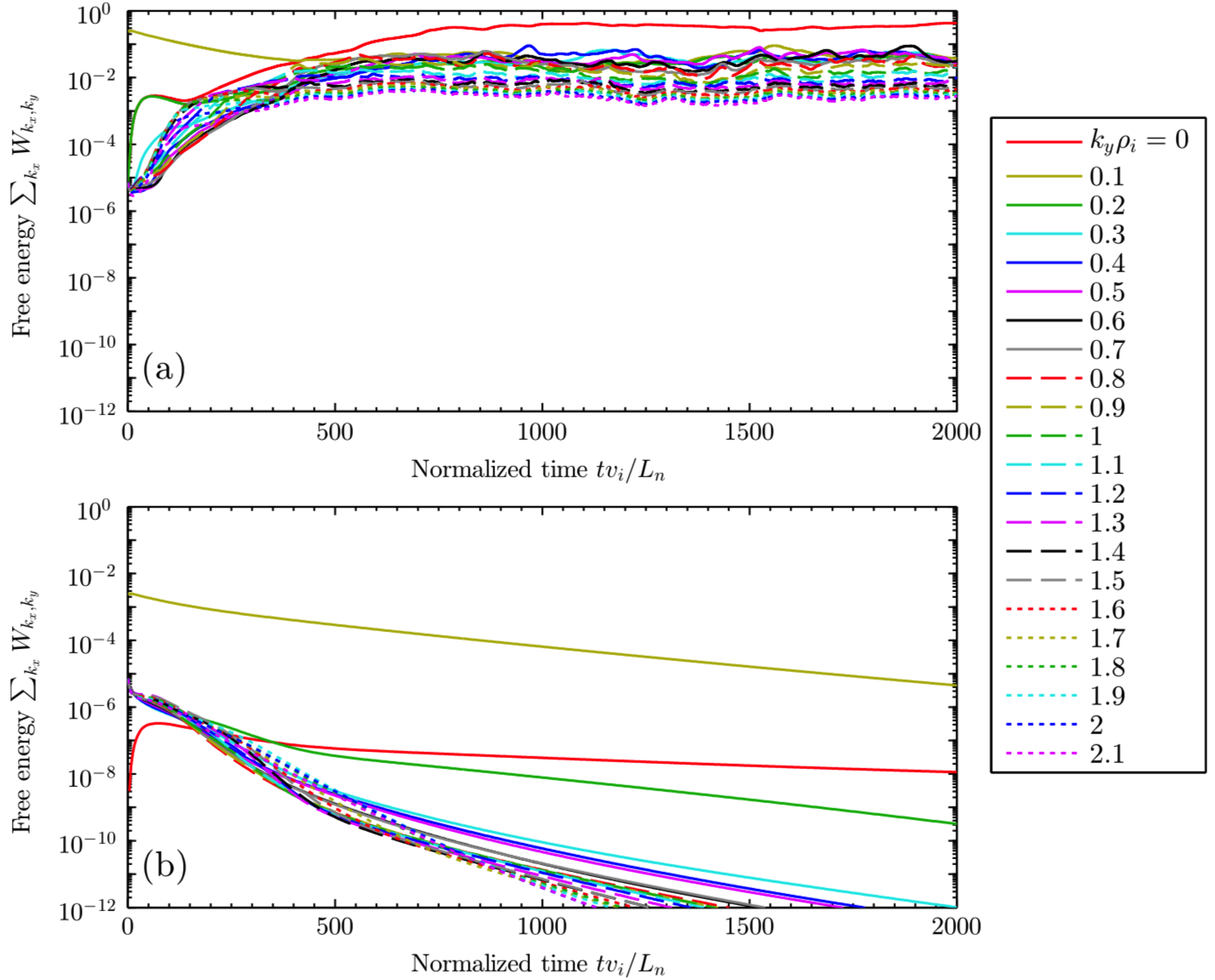
In flows of regular liquids, turbulence often is present even when linear stability analysis indicates that the laminar state should be stable. This “subcritical turbulence” is associated with shear in the flow, which allows structures to grow transiently even though their long-time linear behavior is damped. This kind of subcritical turbulence due to flow shear has also been observed in simulations of plasmas. Drake et al (1995) found that subcritical turbulence can exist in plasmas without shear in the equilibrium flow, if there is shear instead in the magnetic field, using a minimal fluid (non-kinetic) model. Our group recently showed that this turbulence-without-instability from magnetic shear is present also in a rigorous kinetic plasma model (“gyrokinetics”). An example is shown in figure 1: if the system is initialized with small fluctuations they decay due to linear stability, whereas if the same system is initialized with larger fluctuations, turbulence is sustained. We showed this remarkable phenomenon is associated with a discontinuous change in the system’s eigenvalues from unstable to stable as the magnetic shear is changed from zero to a finite value. Nonetheless, the plasma does not realize magnetic shear is present until particles have had time to travel sufficiently far along the field lines, giving the opportunity for large transients that can support subcritical turbulence.

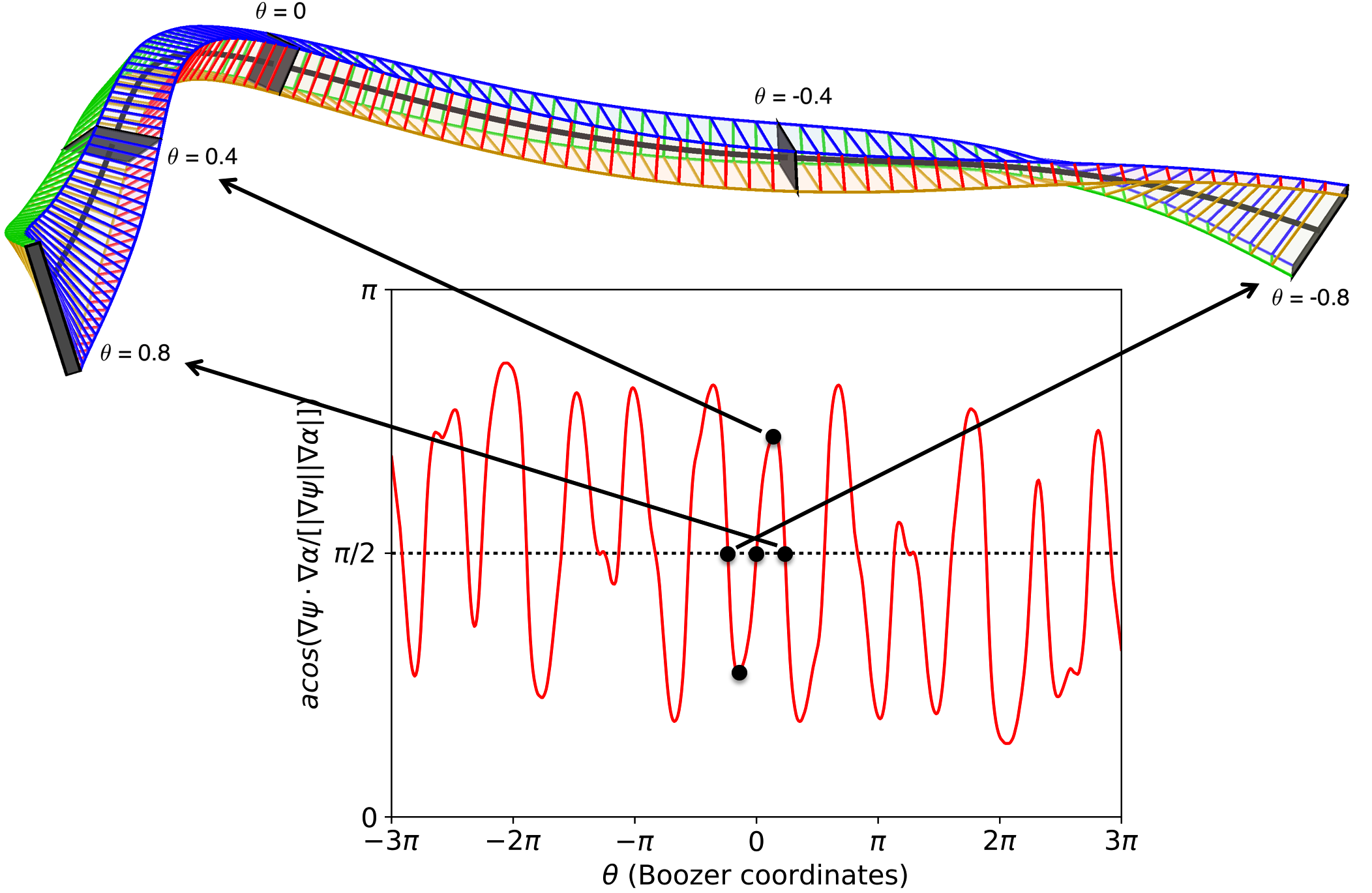
Simulating plasma turbulence in sheared magnetic fields

In magnetized plasmas, turbulence is very anisotropic, with typical fluctuation scales comparable to the gyroradii in the directions perpendicular to the magnetic field, and much longer scale lengths along the field. To model this turbulence efficiently, simulations must be carried out in “flux tubes”, elongated domains that follow the field lines. An example of a flux tube is shown in figure 2. PhD student Mike Martin in our group has developed ways to choose the shape and size of these computational domains to reduce computational cost, while preserving the accuracy of simulations. Due to the boundary conditions, the aspect ratio of the simulation domain in the two transverse directions is linked to the integrated magnetic shear along the tube. Therefore by optimizing the tube length, the ratio of the transverse dimensions can be made close to 1, minimizing the number of Fourier modes needed to resolve the turbulence. Mike showed the choice of tube length can reduce the computational cost of a W7-X turbulence simulation by a factor of 7, and the method is applicable outside of stellarators as well.