Stellarators
Confining plasma with carefully shaped magnetic fields
A stellarator is a magnetic field configuration used to confine plasma, which is a mixture of electrically charged particles such as electrons and ions or positrons. Typically the magnetic field in a stellarator is created using electromagnetic coils. An example of a stellarator is shown in Figure 1.
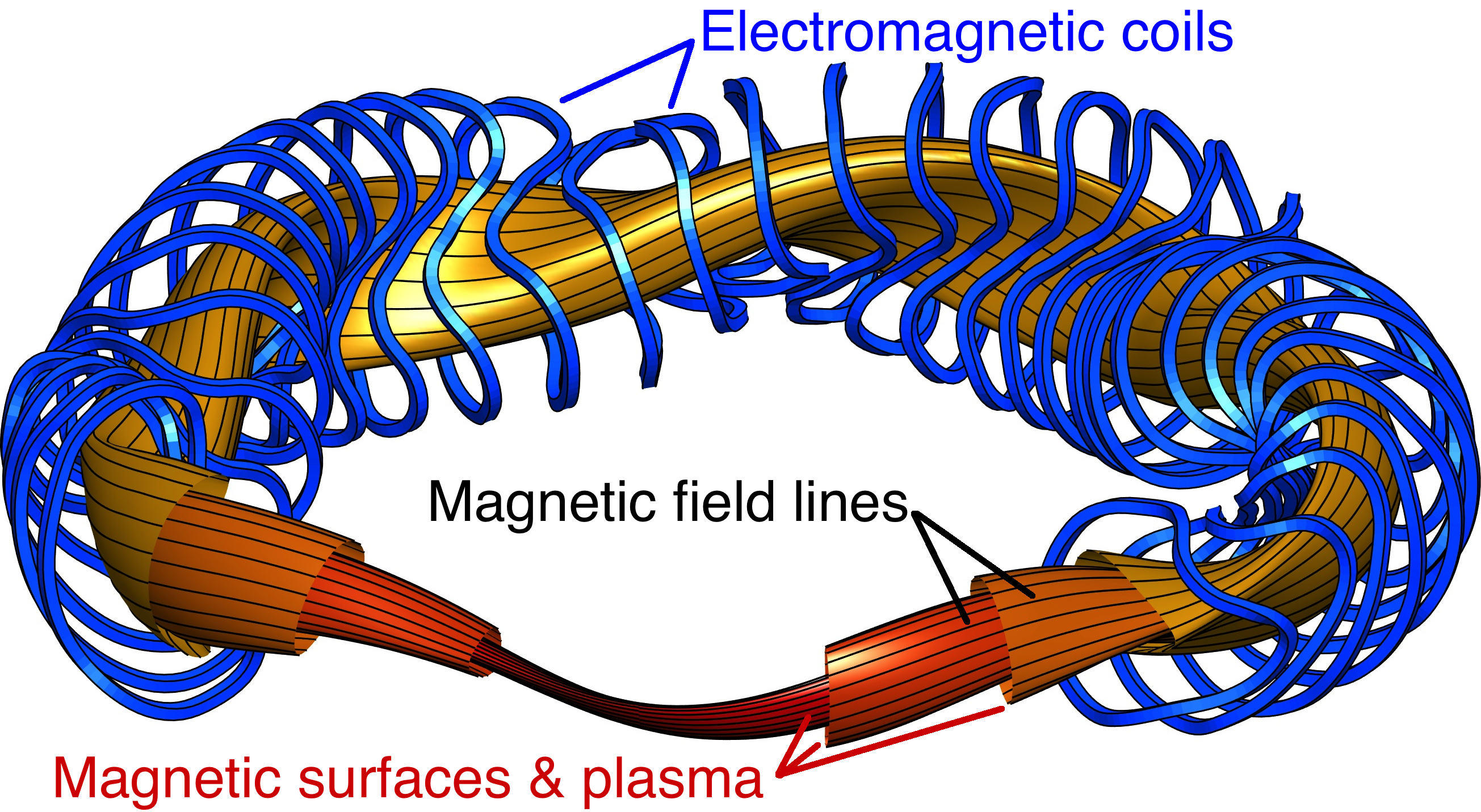
The ability to confine particles has been a transformational tool in physics, associated with multiple Nobel prizes. To confine the particles in a high-temperature plasma, magnetic fields are the best option. Today, stellarators and other magnetic confinement configurations routinely confine plasmas with temperatures exceeding that of the core the sun, and they support temperature gradients 1000x that of the space shuttle’s tiles. One application of stellarators is to create the conditions for fusion, the process that powers stars. If made sufficiently efficient and economical, fusion could provide baseload electricity generation without greenhouse gas production, nuclear proliferation risk, or production of long-lived nuclear waste. Stellarators can also confine electron-positron plasmas relevant to astrophysics.
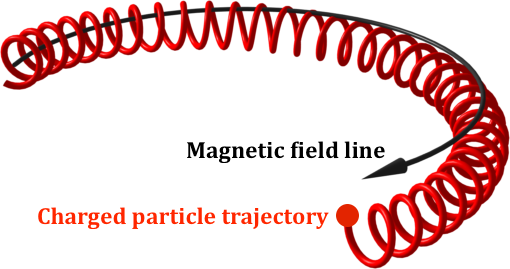
How do the magnetic fields in a stellarator confine particles? To a first approximation, charged particles in a magnetic field B follow helical orbits around the field lines [figure 2]. The radius of the helix can be very small (<= millimeters), so there is confinement perpendicular to B but no confinement along it. To isolate hot plasma from cold, then, the field lines must lie on toroidal nested surfaces [figure 1], called magnetic surfaces or flux surfaces. One approach to achieving these nested surfaces is axisymmetry – continuous rotational symmetry – which is the approach taken in the ‘tokamak’ device, but the axisymmetric approach has important limitations. Ampere’s Law implies as axisymmetric confining magnetic field must have a large internal electric current; this current is hard to drive in steady state and it can provide energy for virulent instabilities. These difficulties are avoided if the true rotational symmetry is replaced by a weaker property with similar consequences to symmetry, ‘integrability’. While general non-axisymmetric magnetic fields have volume-filling field lines, unable to provide confinement since the unconfined particle motion along B connects the inside and outside, carefully optimized non-axisymmetric magnetic fields can have field lines approximately lying on nested surfaces. Such a field is said to be integrable. Field lines in such a field conserve any quantity that is constant on the surfaces, such as the flux of B inside it. Since magnetic field lines have a Hamiltonian structure, the understanding of integrable non-axisymmetric magnetic fields is closely related to general mathematical study of Hamiltonian dynamics. The modeling of integrable magnetic fields is complicated by the fact that there must be a self-consistent equilibrium achieved between Lorentz forces and plasma pressure gradients, and these equilibria have many mathematical subtleties.
A stellarator can therefore be defined as device that confines plasma using an integrable non-axisymmetric magnetic field. There are several stellarators presently operating in the US – at the University of Wisconsin, Auburn University, the University of Illinois, and Columbia University, and there are other stellarators internationally. This is an exciting time for stellarator research, with the recent commencement of the Wendelstein 7-X (W7-X) experiment in Germany, the largest stellarator ever built.
Our group studies several aspects of stellarators. How can the shaping of a stellarator (both the geometry of the magnetic field and the shapes of the coils that produce it) be designed to give the best possible confinement of particles? What are effective numerical methods to compute the distribution function of particles in a stellarator magnetic field? How do electric currents that arise in the plasma modify the magnetic field from the external magnets? How is turbulence in the plasma affected by the geometry of the field, and how can we predict the losses of heat and particles due to this turbulence? How can the problem of stellarator design be formulated in a way that is most convenient for numerical solution?