Neutrino Polarization
-
These days, massless neutrinos are somewhat outdated. Yet, until
right-handed neutrinos are found, and until the speed of neutrinos are
found to be less than c, massless neutrinos will occupy an important place
in physics. Since 1956, they are known to be polarized. Before 1956,
neutrino polarizations were unthinkable because they violate the parity
invariance.
Now the question is whether neutrino polarization is a God-given natural law or is derivable from a more fundamental physical principle. Instead of resorting to God, let us ask Einstein. In 1905, Einstein formulated special relativity with the Lorentz group as the fundamental space-time symmetry of particles.
Among the transformations, in his classic paper of 1939, Eugene Wigner considered subgroups of the Lorentz group which leaves the four-momentum of a given particle invariant. They are called Wigner's little groups these days. These subgroups dictate the internal space-time symmetries of particles in the Lorentz-covariant regime.
For a massive particle, Wigner's little group is locally isomorphic to the three-dimensional rotation group. The particle can be brought to the Lorentz frame in which it is at rest. In this frame, rotations leave its four-momentum invariant.
For a massless particle, the little group is isomorphic to the two-dimensional Euclidean group, consisting of rotations around the origin and two translations. It is not difficult to associate the rotational degree with the helicity of the massless particle. What happens to the two translation degrees of freedom. They correspond to gauge degrees of freedom. Wigner's original 1939 paper does not mention this. After a stormy history, it was finally determined in 1990 that these two translational-like degrees of freedom collapse into one gauge degree of freedom. See also the link on Wigner and Poincaré.
For the spin-1 photon, its four-vector potential is gauge-dependent, and is not directly observable. Its electromagnetic field is gauge-invariant and is directly observable.
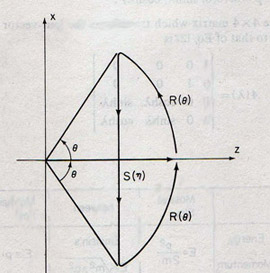
|
| This figure is from Han and Kim, Phys. Rev. A vol. 37, 4494 (1988). |
Of course it is very difficult explain this in the html language without formulas. For a review article, you my visit http://arxiv.org/abs/hep-th/0201262.