Group Contractions
I meet many young physicists who have worked and are working on group contractions. They seem to know my name, but they become totally surprised when I tell them I am also a group contractionist.

|

|
- with Wigner (1986).
- with Inonu (1997). The other gentleman in the photo is Nikolaj Gromov from Russia. He now holds the world championship on group contractions.
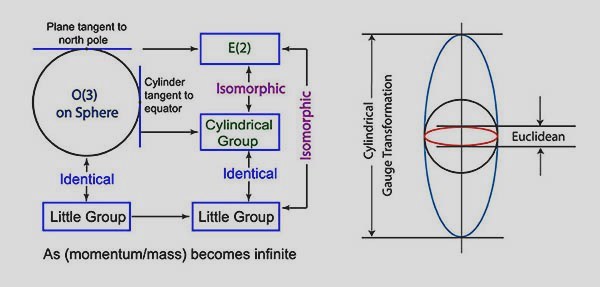
The O(3)-like symmetry for a massive particle corresponds to the spin of the particle. As for the E(2)-like symmetry for a massless particle, it is not difficult to associate the rotational degree of freedom to the helicity. After some stormy history, it has been now established that the two translational degrees of freedom of E(2) correspond to the gauge degree of freedom.
In their 1953 paper [Proc. Nat. Aca. Sci. 39, 510], Inonu and Wigner showed that O(3) can be contracted to E(2) by a north-pole approximation, or by considering a flat-surface tangent to the north pole of the earth.
Then the following question arises. Can the E(2)-like little group for massless particles be obtained from the O(3)-like little group by a group contraction procedure. The answer to this question is YES.
- Y. S. Kim and E. P. Wigner, "Cylindrical group and massless
particles," J. Math. Phys. Vol. 28, pages 1175-1179 (1987).
Click here for the paper.
- Y. S. Kim and E. P. Wigner, "Space-time geometry of relativistic
particles," J. Math. Phys. Vol. 31, pages 55-60 (1990).
Click here for the paper.
-
Inonu's review paper given at the
Workshop on Quantum Groups, Deformations and Contractions
(Istanbul, Turkey, 1997).
-
Kim's paper presented at the same Workshop after
Inonu's talk.
These figures are from the above-mentioned the papers by Kim and Wigner (1987 and 1990).
Often you see the following table from my conference talks and published papers. This table tells what physical role the group contraction plays in unifying the symmetries of massive and massless particles.
| ||||
| ||||
| ||||
|
- copyright@2015 by Y. S. Kim, unless otherwise specified.

| |
|