Quantum Mechanics: from Galilei to Einstein

• In quantum mechanics, free particles are running waves, and extended objects consist of standing waves.

  Of course, there have been many attempts to make quantum mechanics consistent with consistent with special relativity. Quantum field theory is a giant step toward this goal. In this theory, we are led to calculate the Lorentz-covariant S matrix. We can compute the S-matrix elements using Feynman diagrams. However, all Feynman diagrams have legs corresponding to free particles. This means that the S matrix is designed for dealing with scattering processes.

• How about bound states? Can we use Feynman diagrams for computing bound-state problems? Indeed, there have been efforts to deal with bound-state problems in terms of poles in analytic S matrices. However, we do not know how to deal with boundary conditions of the wave function in this S-matrix approach. In fact, there is a concrete example which will lead to a disaster in the S-matrix method for dealing with bound-state problems. You may click here for a concrete example.

  In 1970, Feynman suggested that, instead of Feynman diagrams, we may use harmonic oscillators for Lorentz-covariant bound-state problems, and published a paper with his students in 1971.

  However, Feynman and his co-authors did not use correct mathematics to satisfy all the known physical laws of quantum mechanics and special relativity. Is it possible possible to correct their mathematical errors?

  Yes, it is possible if we import Wigner's mathematics. In 1939, Wigner published a paper on the subgroups of the Lorentz group invariant. Wigner considered the maximal subgroup of the Lorentz group which leaves the four-momentum of a given particle invariant. These subgroup is called Wigner's little group. While the Lorentz group has six independent parameters, the little group has only three parameters. For a massive particle, there is a Lorentz frame in which the particle is at rest. In this frame, the little group is the three-dimensional rotation group.

  Likewise, for an extended object consisting of standing waves, its boundary condition has a three-dimensional rotational symmetry. With this point in mind, we can construct a representations of the little group using harmonic oscillator wave functions. Click here for a paper on this subject.

• We should note also that Paul A. M. Dirac spent much of his research time to construct harmonic oscillator wave functions in the Lorentz-covariant world. Dirac was not capable of making mathematical errors, but his papers have to be linked up in a systematic manner to describe standing waves in in the Lorentz-covariant world. This can also be achieved within the framework of Wigner's representation of the little groups.

  Thus, after appropriate fix-ups, Feynman's oscillator wave functions should satisfy the Lorentz-covariant boundary conditions dictated by the symmetry of Wigner's little group.

  Since Wigner's little groups are subgroups of the Lorentz group, Einstein prevails both insider and outside the particle.

  ---

  There is at least one set of wave functions which satisfies the Lorentz-covariant boundary conditions, and which can be placed in Step 1 of the Comet/Planet table given at right. It is indeed gratifying to be fill in this step using only the existing principles of quantum mechanics and relativity. We did not have to invent any new physics. The next step is to construct one mathematical device which will take care of both scattering and bound states.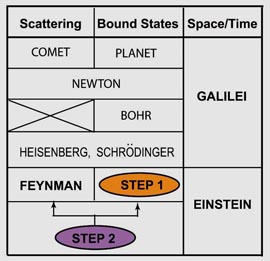

  The most cruel question is whether this covariant bound-state wave function can explain anything in the real world. Click here for an interesting story.

  Y. S. Kim (7 November 2006)

Why is he with Einstein?

• copyright@2006,2015 by Y. S. Kim, unless otherwise specified.
  
  1. Click here for his home page.
     

  2. His Einstein page.
  3. His Princeton page.

  4. His style page.
  5. His stories.