Two Famous Brothers-in-law

|
| Dirac and Wigner, photo from AIP Emilio Segre Visual Archives |

|
Wigner asked me whether I knew Paul A. M. Dirac passed away. He said he became very sad because he lost his famous brother-in-law. I told him I attended his memorial service held at Florida Sate University in November of 1984. He then told me there is Dirac's bust in the Fine Hall Library (for mathematics and physics), and asked me whether I would be interested going there with him to see the bust. Here is a photo of the bust.
In order to tell the stories Wigner wanted to hear, I had written a book, entitled "Theory and Application of the Poincaré Group with Marilyn Noz who has been my colleague since 1970. It was one year before the book was published in 1986, but I had a typed set of manuscript by 1985. The LaTex was not available at that time.
This book is about Wigner's 1939 paper on his little groups dealing with internal space-time symmetries of particles in the Lorentz-covariant world. I thank Mariano del Olmo for writing a very accurate review of this book. His review contains the following paragraph.
Note that E. P. Wigner's noteworthy paper [Ann. Math. (2)40 (1939), 149-204] was the source of inspiration for the authors when writing this book. There is also a remarkable trace of some of Dirac's papers in this book.
Yes, we wrote this book based on the papers we had written on Wigner's little groups before 1984, and I was ready to talk with Wigner. I was also ready to talk him about some important papers written by Dirac, who was Winger's famous brother-in-law. This is precisely why I was able to tell the stories Wigner wanted to hear. I has no other magic. Wigner was known as one of the most difficult persons to talk to.
Since then, I studied Dirac's papers more systematically. These days, my papers are mostly about Dirac's works. I still work with Marilyn Noz.
When I had a private audience with Dirac in 1962, he told me American physicists should spend more time on understanding Lorentz covariance. At that time, he was working on or had just finished 1963 his paper on A remarkable representation of the O(3,2) deSitter group, which describes the Lorentz group with two coupled harmonic oscillators. Like all other papers by Dirac, it is a beautiful mathematical piece. But can we extract physics from this paper?
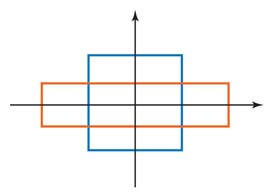 The best way to decode this paper is to have a simple graphical desciption.
For two coupled ocillators, we are led to use the normal coordinate system
where one coordinate expands and the other shrinks, as shown in the
figure. The same geometrical interpretation can be given to the Lorentz
boosts in the light-cone coordinate system
which Dirac presented in his 1949 paper on
Forms of
relativistic dynamics.
The best way to decode this paper is to have a simple graphical desciption.
For two coupled ocillators, we are led to use the normal coordinate system
where one coordinate expands and the other shrinks, as shown in the
figure. The same geometrical interpretation can be given to the Lorentz
boosts in the light-cone coordinate system
which Dirac presented in his 1949 paper on
Forms of
relativistic dynamics.
 The rectangle given here indeed combines the physics of coupled harmonic
oscillators and the physics of Lorentz transformations. Methematicians
made the subject difficult for physicists by combinining this rectangular
or squeeze transformation with rotations. This then becomes a symplectic
(Lorentz group is a cousin of this group), but we should not be
afraid of this word. Are you afraid of rectangles? Are you afraid of
coupled oscillators?
The rectangle given here indeed combines the physics of coupled harmonic
oscillators and the physics of Lorentz transformations. Methematicians
made the subject difficult for physicists by combinining this rectangular
or squeeze transformation with rotations. This then becomes a symplectic
(Lorentz group is a cousin of this group), but we should not be
afraid of this word. Are you afraid of rectangles? Are you afraid of
coupled oscillators?
Mathematically speaking, modern physics is the physics of harmonic oscillators or/and two-by-two matrices, since otherwise problems are not soluble. Dirac was quite fond of harmonic osicllators as we can see from his papers, and Wigner always demanded young people to explain things in terms of two-by-two matrices. Thus, the mathematics of two coupled harmonic oscillator is the closest thing to the "theory of everything."
The Lorentz boost is the basic ingredient of high-energy physics. Dirac's formulation of coupled harmonic oscillators forms the basic language for modern quantum optics, dealing with squeezed states, entangled state, as well as decoherence. Click her for details.
If you think what I said above is too dry for the New Year, you are invited to read the following story about how Dirac and Wigner became brothers-in-law.
Wigner's Sisters
-
Wigner used to say Dirac was "my famous brother-in-law." Indeed,
Dirac married Wigner's younger sister. Interesting?