Appendix M: Curve fitting in spreadsheets and stand-alone programs. 


Both Excel and OpenOffice Calc have a "Solver" capability that will change specified cells in an attempt to produce a specified goal; this can be used in peak fitting to minimize the fitting error between a set of data and a proposed calculated model, such as a set of overlapping Gaussian bands. (This external source, https://www.wallstreetmojo.com/solver-in-excel/, has a detailed graphical explanation of using the Solver.) Solver includes three different solving methods. 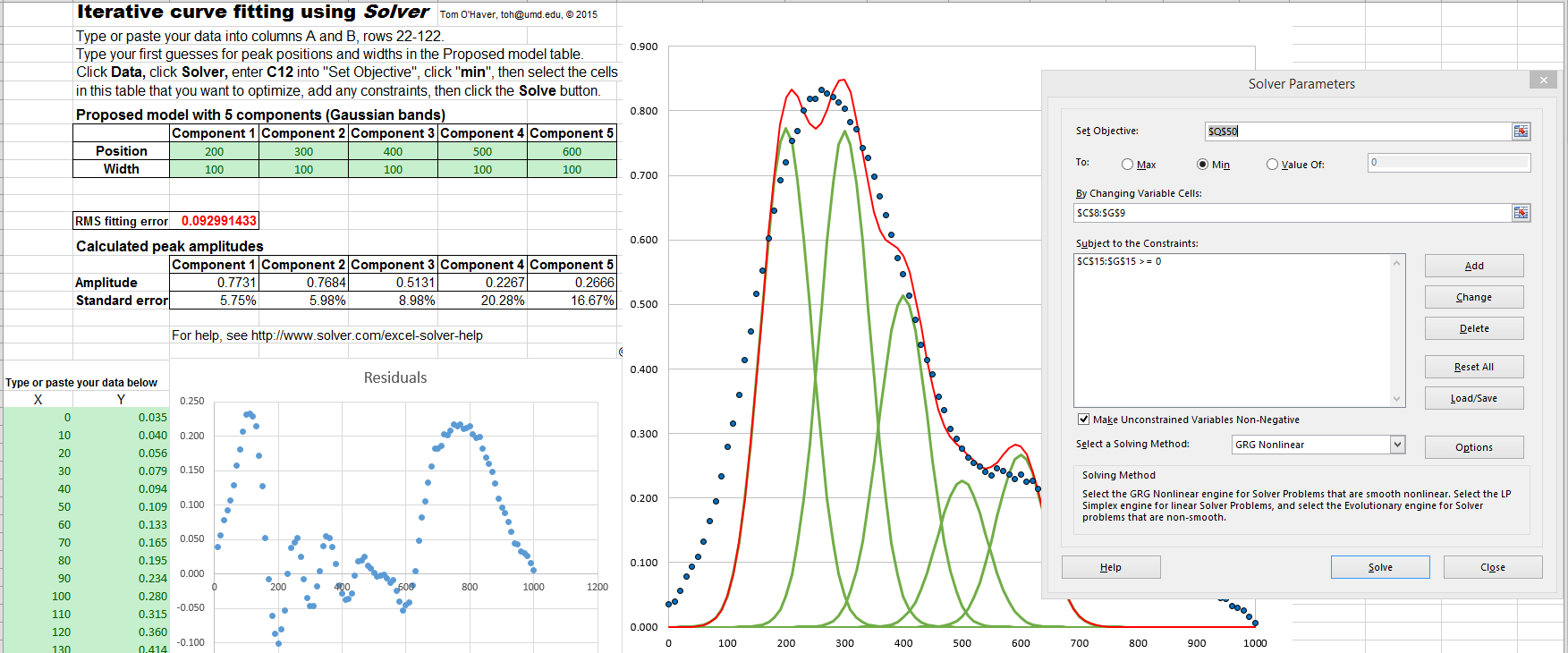This Excel spreadsheet example (screen shot) demonstrates how this is used to fit four Gaussian components to a sample set of x,y data that has already been entered into columns A and B, rows 22 to 101 (you could type or paste in your own data there).  


After entering the data, do a visual estimate of how many Gaussian peaks it might take to represent the data, and their locations and widths, and type those values into the 'Proposed model' table. The spreadsheet calculates the best-fit values for the peak heights (by multilinear regression) in the 'Calculated amplitudes' table and plots the data and the fit. It also plots the "residuals", which are the point-by-point differences between the data and the model; ideally the residuals would be zero, or at least small. (Adjust the x-axis scale of these graphs to fit your data). The next step is to use Solver function to "fine-tune" the position and width of each component to minimize the % fitting error (in red) and to make the residuals plot as random as possible: click Data in the top menu bar, click Solver (upper right) to open the Solver box, into which you type "C12" into "Set Objective", click "min", select the cells in the "Proposed Model" that you want to optimize, add any desired constraints in the "Subject to the Constraints" box, and click the Solve button. The position, width, and amplitude of all the components are automatically optimized by Solver and best fit is displayed. (You can see that the Solver has changed the selected entries in the proposed model table, reduced the fitting error (cell C12, in red), and made the residuals smaller and more random). If the fit fails, change the starting values, click Solver, and click the Solve button. You can automate the above process and reduce it to a single function-key press by using macros, as described in Appendix N.

So, how many Gaussian components does it take to fit the data? One way to tell is to look at the plot of the residuals (which shows the point-by-point difference between the data and the fitted model), and add components until the residuals are random, not wavy, but this works only if the data are not smoothed before fitting. Here's an example - a set of real data that are fit with an increasing sequence of two Gaussians, three Gaussians, four Gaussians, and five Gaussians. As you look at this sequence of screenshots, you'll see the percent fitting error decrease, the R2 value become closer to 1.000, and the residuals become smaller and more random. (Note that in the 5-component fit, the first and last components are not peaks within the 250-600 x range of the data, but rather account for the background). There is no need to try a 6-component fit because the residuals are already random at 5 components and more components than that would just "fit the noise" and would likely be unstable and give a very different result with another sample of that signal with different noise.

There are a number of downloadable non-linear iterative curve fitting adds-ons and macros for Excel and OpenOffice. For example, Dr. Roger Nix of Queen Mary University of London has developed a very nice Excel/VBA spreadsheet for curve fitting X-ray photoelectron spectroscopy (XPS) data, but it could be used to fit other types of spectroscopic data. A 4-page instruction sheet is also provided.

The Python language has many options for iterative least-squares; one is is compared to its Matlab equivalent.

There are also many examples of stand-alone freeware and commercial programs, including PeakFit, Data Master 2003, MyCurveFit, Curve Expert, Origin, ndcurvemaster, and the R language.

If you use a spreadsheet for this type of curve fitting, you have to build a custom spreadsheet for each problem, with the right number of rows for the data and with the desired number of components. For example, my CurveFitter.xlsx template is only for a 100-point signal and a 5-component Gaussian model. It's easy to extend to a larger number of data points by inserting rows between 22 and 100, columns A through N, drag-copying the formulas down into the new cells (e.g. CurveFitter2.xlsx is extended to 256 points). To handle other numbers of components or model shapes you would have to insert or delete columns between C and G and between Q and U and edit the formulas, as has been done in this set of templates for 2 Gaussians, 3 Gaussians, 4 Gaussians, 5 Gaussians, and 6 Gaussians.

If your peaks are superimposed on a baseline, you can include a model for the baseline as one of the components. For instance, if you wish to fit 2 Gaussian peaks on a linear tilted slope baseline, select a 3-component spreadsheet template and change one of the Gaussian components to the equation for a straight line (y=mx+b, where m is the slope and b is the intercept). A template for that particular case is CurveFitter2GaussianBaseline.xlsx (graphic); don't click "Make Unconstrained Variables Non-Negative" in this case, because the baseline model may well need negative variables, as it does in this particular example. If you want to use another peak shape or another baseline shape, you'd have to modify the equation in row 22 of the corresponding columns C through G and drag-copy the modified cell down to the last row, as was done to change  the Gaussian peak shape into a Lorentzian shape in CurveFitter6Lorentzian.xlsx. Or you could make  columns C through G contain equations for different peak or baseline shapes. For exponentially broadened Gaussian peak shapes, you can use CurveFitter2ExpGaussianTemplate.xlsx or two overlapping peaks (screen graphic). In this case, each peak has four parameters: height, position, width, and lambda (which determines the asymmetry - the extent of exponential broadening).
 
In some cases, it is useful to add constraints to the variables determined by iteration, for example to constrain them to be greater than zero, or constrained between two limits, or equal to each other, etc. Doing so will force the solutions to adhere to known expectations and avoid nonphysical solutions. This is especially important for complex shapes such as the exponentially broadened Gaussian just discussed in the previous paragraph. You can do this by adding those constraints using the "Subject to the Constraints:" box in the center of the "Solver Parameters" box (see the graphic above). For details, see https://www.solver.com/excel-solver-add-change-or-delete-constraint?

The point is that you can do - in fact, you must do - a lot of custom editing to get a spreadsheet template that fits your data. In contrast, my Matlab/Octave peakfit.m function automatically adapts to any number of data points and is easily set to over 40 different model peak shapes and any number of peaks simply by changing the input arguments. Using my Interactive Peak Fitter function ipf.m in Matlab, you can press a single keystroke to instantly change the peak shape, number of peaks, baseline mode, or to re-calculate the fit with different start or with a bootstrap subset of the data. That's far quicker and easier than the spreadsheet. But on the other hand, a real advantage of spreadsheets in this application is that it is relatively easy to add your own custom shape functions and constraints, even complicated ones, using standard spreadsheet cell formula construction. And if you are hiring help, it's probably easier to find an experienced spreadsheet programmer than a Matlab programmer. So, if you are not sure which to use, my advice is to try both methods and decide for yourself.

This page is part of "A Pragmatic Introduction to Signal Processing", created and maintained by Prof. Tom O'Haver , Department of Chemistry and Biochemistry, The University of Maryland at College Park. Comments, suggestions and questions should be directed to Prof. O'Haver at toh@umd.edu. Updated July, 2022.