

Animated Diffraction grating
Microsoft Excel and OpenOffice Calc Versions
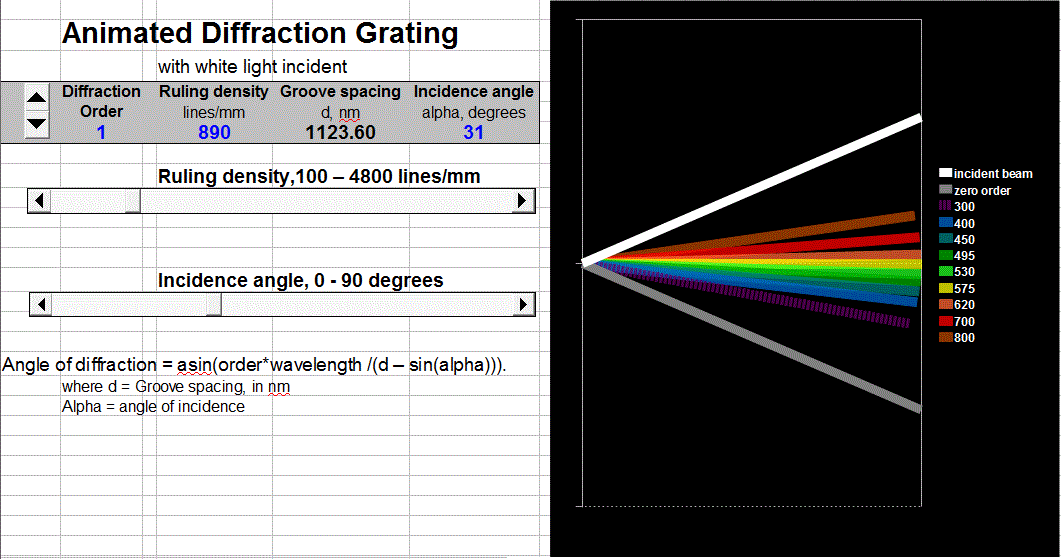 |
Animated model of a plane diffraction grating, with sliders to control the angle of incidence, the ruling density, and the diffraction order viewed. Based on the grating equation: Angle of diffraction = asin(order*wavelength /(groove spacing) - sin(angle of incidence)).
Assumptions: The grating surface is represented by the striped bar on the left of the figure. It is illuminated with a thin parallel, collimated "white" light beam consisting of eight discrete wavelengths. Only one diffraction order is shown at a time (selected by the number wheel). Only eight wavelengths are shown in the diffracted beam. The colors of the diffracted beams roughly match the wavelengths of those beams. The relative intensity of different wavelengths and orders is not represented. For clarity, narrow beams are shown, even though in practical applications a wide beam, entirely covering the grating surface, is ordinarily used. Angles are measured from the horizontal axis.
Fixed grating with variable angle of incidence
Download spreadsheet in Excel format (.xls)
Download spreadsheet in OpenOffice format (.ods)
Rotating grating (as in Ebert or Czerny-Turner mounting), shown above.
Download spreadsheet in Excel format (.xls)
Download spreadsheet in OpenOffice format (.ods)
There is also an alternative version with 4 different pairs of wavelengths separated by 1 nm, useful for demonstrating the conditions leading to the highest dispersion. The angular dispersion of a grating is determined by differentiating the diffraction angle with respect to wavelength and is equal to order*(ruling density) /cos(angle of diffraction), where the ruling density is the number of grating lines per unit length. As the angle of diffraction approaches 90º, its cosine approaches zero, and the angular dispersion approaches infinity. So the dispersion is expected to be greatest for whatever wavelength is diffracted close to 90º. Of course, you can't actually use a diffraction angle of 90 degrees, but you should be able to get close. If you achieve a sufficiently high angular resolution, you'll be able to separate the diffracted beams into two close-spaced wavelengths. Try it!
Download spreadsheet in OpenOffice format (.ods)
Wingz Version
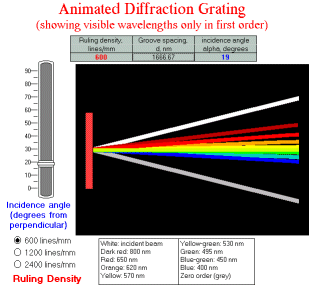
WingZ version Grat1.wkz
[OpenOffice and Excel Versions]