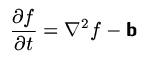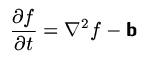Source file multigrid.M

cat multigrid.M | m4

1. pre-smoothing: The simplest smoother is a Jacobi smoother which can be regarded as an explicit time stepper for the diffusion equation
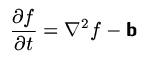
with the time step adjusted to the shortest wavelength. A small number a pre-smoothing steps is performed (usually 3-5).
2. calculation of the defect: b_coarse = div grad f - b; since short wavelength have been efficiently smoothed the defect mainly consists of long wavelength components and therefore can be well represented on a coarser grid.
3. restriction of defect: the defect is mapped to a coarser grid
4. recursive call: the multigrid is called recursively to treat the Poisson equation on the coarser grid and to obtain a coarse grid solution f_coarse to the Poisson equation div grad f_coarse= b_coarse. Either one or two recursive calls can be applied, the first case is called a V-cycle, the second case a W-cycle.
5. prolongation: the solution for the Poisson equation on the coarse grid f_coarse is interpolated and subtracted from the fine grid solution f.
6. post-smoothing: finally again a small number a smoothing steps is performed using the same algorithm as for the pre-smoother

Subroutines:

• Subroutine poisson:

This is the main entry point if the multigrid is used as a Poisson solver for the equation div grad f = b. The iteration is terminated if the residual (the defect) is smaller than a predefined value, or the entire code is aborted if convergence cannot be reached with the admitted number of iterations.
• Subroutine helmholtz:

This is the main entry point for using the multigrid as a Helmholtz solver for the equation (1-d_e² div grad) f = b.
• Subroutine multigrid:

The subroutine multigrid controls the execution and termination of the multigrid solver, it contains the outer iteration loop, checks the progress towards convergence, and initiates the multigrid recursion.
• Subroutine set mg3d_...:

The subroutines mg3d_0, mg3d_1, mg3d_2, ... contain the operations to be performed at each grid level as described above. They are generated from the template mg3d_$1 by the preprocessor m4. At each level the number of grid points is reduced by a factor of two in all spatial directions compared to the previous level.
• Subroutine set mg3dxy_...:

The mg3d_... grid-hierarchy stops when in one spatial direction only one grid point per processor is left. Since this would preclude operation in 2-D mode the code proceeds with a two-dimensional treatment when only one grid point per processor is left in the z direction. The hierarchy mg3dxy_... therefore is very similar to mg3d_... but the grid is coarsened only in the x and y directions.
• Function res3d:

The function res3d calculates the residual of the approximate solution to obtain a measure for the total error. The sum over all grid points of the quantity abs(div grad f -b) or abs[(1-d_e² div grad) f - b] taken in the Poisson or Helmholtz case. As an option the total sum is divided by the number of grid points and the squared speed of light in the Poisson case and by the number of grid points in the Helmholtz case. The result is used by the driver routine multigrid to decide whether to continue or to terminate the multigrid iteration.
• Subroutine sor:

Once only one grid point per processor is left in the x and y direction the multigrid hierarchy stops. In the Poisson case the remaining coarse grid problem is treated either by an increased number of smoothing iterations or with a successive over relaxation. The successive over relaxation is implemented in the subroutine sor. In the Helmholtz case increasing the number of smoothing iterations is the only option implemented so far.

• For best multigrid performance the hierarchy should stop at a very coarse grid, there nx and ny should be similar.
• The smoothers currently implemented completely fail unless the resolution in all spatial directions is very similar, i.e. dx=dy=dz
• For the coarsening two different strategies can be applied:
Strategy (a) works only for periodic boundary conditions. Strategy (b) works always but converges more slowly. In case periodic boundary conditions are applied it is therefore recommended to switch from the default strategy (b) to (a) by using the switch alt_restrict_prolong.

• miniter: The parameter miniter defines the minimum number of multigrid operations that are performed regardless of the size of defect (to avoid that in pathological situations the multigrid is not called at all). Typically #define miniter 3 is fine.
• fixiter: In the two-fluid and the hybrid version the multigrid can be called in a reduced version with a prescribed number of iterations to save the time for calculating the residual. Full convergence is enforced only at each n^th time step. In the two-fluid version n is set by the parameter fixedsteps. In the hybrid version the multigrid solver is called with a prescribed number of fixiter iterations during the substeps of the fluid part, whereas convergence of the helmholtz equation is enforced only when the particle ions are stepped. In the full-particle version this parameter has no effect. A reasonable value is  #define fixiter 2.
• fixedsteps: In the two-fluid version of the code the parameter fixedsteps determines during how many time steps the multigrid is called with a prescribed number of iterations (see parameter fixiter), before full convergence is enforced. In the hybrid and the full-particle versions this parameter is meaningless. A reasonable value is #define fixedsteps 5.
• maxiter: The maximum number of multigrid iterations should be limited to enforce termination, if the multigrid fails to converge. This can happen for example if the parameter eps (see below) is too small to achieve convergence within the finite floating point precision. If convergence is not obtained after maxiter iterations the entire code is aborted. A reasonable value is #define maxiter 1000
• WCYCLE: As default configuration a V-cycle is applied. With the switch #define WCYCLE the multigrid performs a W-cycle.
• GS_LEX, GS_RB, JACOBI: Besides the Jacobi-smoother described above, Gauss-Seidel smoother can be applied either with lexicographical or with red-black-ordering. The default smoother is JACOBI, to explicitly choose the smoother use the switches #define GS_LEX, #define GS_RB, #define JACOBI.
• nu1, nu2, nu3: The parameter nu1 is the number of pre-smoothing steps, nu2 the number of post-smoothing steps and nu3 the number of additional smoothing iteration at the coarsest grid. If coarsegrid_sor is switched on nu3 sets the number of SOR iterations. Typical values are #define nu1 4, #define nu2 4, #define nu3 20.
• eps: The parameter eps defines the maximum admitted size of the residual. In combination with the switch norm_res a typical value for the Poisson case would be #define eps 1e-11 and for the Helmholtz case #define eps 1e-5.
• norm_res: If the switch #define norm_res is used the residual is normalized in the function res3d as described above, otherwise just the total sum is return without any normalization.
• alt_restrict_prolong: The switch #define alt_restrict_prolong switches to restriction strategy (a) as described above instead of using the default (b). It is recommended to use this switch in combination with periodic boundary conditions.
• coarsegrid_sor: The switch #define coarsegrid_sor enables the use of the successive over relaxation on the coarsest grid in the Poisson case, it has no effect in the Helmholtz case.
• mg_verbose: With the switch #define mg_verbose the multigrid prints some statistics after each invocation. Use the switches mg_verbose and mg_verbose2 if unsure about correct multigrid operation and/or performance.
• mg_verbose2: If the switch #define mg_verbose2 is used the residual is printed after each multigrid iteration.