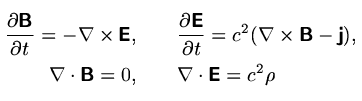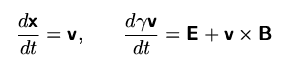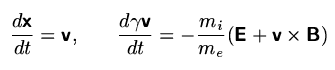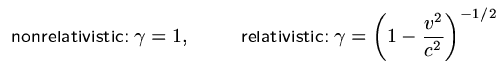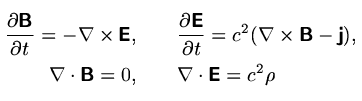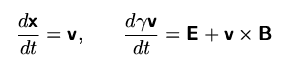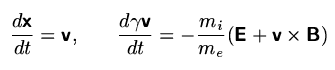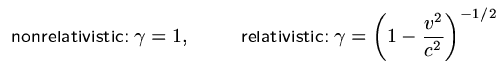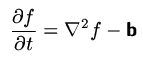Full particle code

This paragraph briefly summarizes the general features of the full-particle code, including the underlying equations, the numerical algorithms for the particle dynamics and Maxwell's equations, the multigrid algorithm for Poisson's equation and the domain decomposition.

General features

The code advances the full Maxwell equations and the individual ions and electrons. For the motion of the particles the user can choose between the non-relativistic and the relativistic equation of motion. The dynamics of the electric and the magnetic are determined by Faraday's and Ampere's laws and the current density which results from the particles' positions and velocities. Although Poisson's equation should remain satisfied automatically discretization errors in the continuity equation may accumulate to a secular violation, therefore the electric field needs to be corrected regularly. The associated Poisson equation is solved in real space employing a multigrid algrorithm and allowing for general non-periodic boundary conditions. The data and the computational work are distributed following a 3-D domain decomposition and all communication is performed with MPI routines.

Equations

The equations are normailzed to the ion cyclotron frequency and the ion inertial length at reference density and magnetic field. The remaining parameters are the ratio between the speed-of-light and the Alfven-velocity and the ratio between electron and ion mass. This leads to the following set of equations for the relativistic and the non-relativistic cases.

Maxwell's equations in normalized form (c=normalized speed of light c/v_A)

equation of motion for the ions

equation of motion for the electrons

parameter gamma in the relativistic/ non-relativistic equation of motion

Numerical techniques - Particle dynamics

The particles positions and momenta are advanced according to the Boris algorithm, which basically consists of the following steps:

advance position with last value for the velocity for half of total time step dt/2
advance velocity for full time step dt

advance velocity for half of total time step dt/2 according to electric force

v_new= v_old+ E dt/2

advance velocity for full time step dt according to magnetic force

v_new - dt/2 (v_new x B) = v_old + dt/2 (v_old x B)

advance velocity for half of total time step dt/2 according to electric force

advance position with present velocity for time dt/2

For further details see: C. K. Birdsall, A. B. Langdon, Plasma Physics via Computer Simulation, IOP Publ., Bristol, 1991

Numerical techniques - Maxwell's equations

Faraday's and Ampere's laws are advanced with an explicit trapezoidal leapfrog algorithm, where all spatial derivatives are taken to second order. Although the dynamics of the electric field is fully determined by Faradays' law a Poisson quation should be solved: Faraday's law dE/dt = c²(curl B - j) implies d/dt (div E) = c² div j = c² d/dt rho provided the particle motion exactly satisfies the equation of continuity. Thus except for discretization errors Farady's law and the equation of continuity guarantee that Poisson's equation remains satisfied if it was satisfied initially. Discretization errors in the continuity equation however may accumulate to a secular violation of Poisson's equation. To correct for this errors one needs to solve the Poisson equation div grad phi = div E - c²rho. The corrected electric field E' = E - grad phi then exactly satisfies Poisson's equation.

Numerical techniques - Multigrid Poisson solver

The Poisson equation is treated with a multigrid solver, since a multigrid algorithm parallelizes very well and does not require Fast-Fourier-Transformations which would enforce periodic boundary conditions. A standard iterative solver substitutes the Poisson equation by a diffusion equation.

The steady state solution then solves the Poisson equation. Advancing the diffusion by an explicit stepping algorithm requires very small time steps, since according to the Courant criterion the time step dt is linked to the smallest scales dt < dx² . Since the large scales modes relax very slowly (relaxation proportional to exp{-k² t}) a prohibitively large number of time steps is required. The basic idea of the multigrid algorithms is to treat the large scale modes on a coarser grid. Small scale modes being absent a larger time step can be chosen since dx is larger. Proceeding recursively from fine to coarse grids and backwards each scale lenght is relaxed on the grid with the appropriate resolution leading to the name multigrid.

For further details see: U. Trottenberg, C. Oosterlee, A. Schüller, Multigrid, Academic Press, London, 2001

Domain decomposition

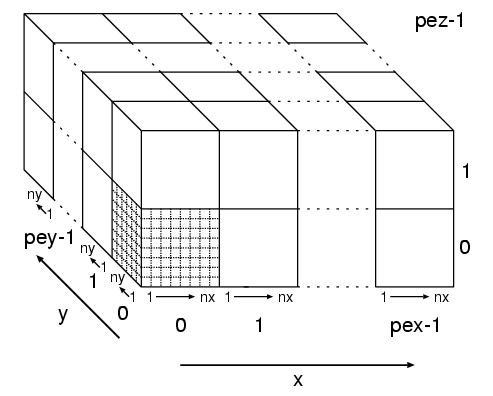
To efficiently use a very large number of processors on a distributed memory machine a three-dimensional domain decomposition is used. pex, pey, pez denote the number of processors in the x,y,z directions whereas nx,ny,nz are the number of grid points within the subdomain treated by one processor. Thus, the total number of grid points per processors is given by nx x ny x nz, the total number of processors is n_pes = pex x pey x pez and the total number of grid points is nx x pex x ny x pey x nz x pez.

Real grid points range from x=1,...,nx whereas x=0 and x=nx+1 represent layers of ghost cells which are used to link the domains of neighboring processing elements. Each particle is treated by the processor that treats the spatial subdomain in which particle is located. If the particle leaves this domain it is transfered to the appropriate processor. Obviously a large density variation can lead to load imbalance and therefore a performance degradation.