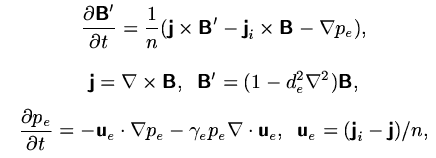Hybrid code

The hybrid code is largely identical with the full particle code. Instead of solving the Maxwell equations and the equation of motion for individual electrons the electrons are replaced by a massive fluid with isotropic pressure and the electron density is equated with the ion density assuming quasi-neutrality. The Helmholtz equation that arises in the fluid equations is inverted with a multigrid algorithm very similar to the one described in section for the full particle code. For the ion dynamics and the domain decomposition the same approaches are used as in the full particle code.

Equations

The dynamics of the electron fluid and the magnetic field follows from the equations (compare M. A. Shay, J. F. Drake, B. N. Rogers, Journal of Geophys. Res. 106, 3759, 2001)

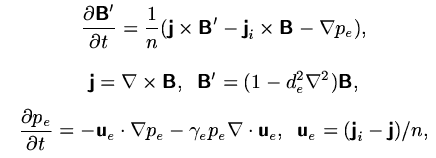
with the electron skin depth d_e. In the equation of motion for the individual ions a simplified electric field is used

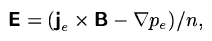
where the electron inertia term is neglected.

Numerical algorithms

Particle density and ion current density result from the ion particle dynamics and enter the fluid equations as external quantities. The basic field quantities which have to be advanced according to the fluid equations are B' and the electron pressure p_e. For the time stepping a trapoezoidal leapfrog algorithm is used as for the Maxwell equations in the full particle version. After advancing B' the magnetic field B is obtained by inverting the Helmholtz equation

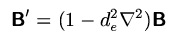
For this purpose the same multigrid algorithm as for the particle code is used.