Zoology 421 Neuron simulations:

Exercise 4. Passive Transmission Along Axons and Dendrites

PLEASE PRINT OUT THESE PAGES FIRST AND THEN KEEP THE PRINTED TEXT BESIDE YOU AS A GUIDE WHEN YOU LOAD AND RUN "NEURON". THIS WILL SAVE YOU HAVING TO JUGGLE BETWEEN NEURON AND NETSCAPE WINDOWS ONCE YOU HAVE THE SIMULATION LOADED.

To begin working with this chapter you should have downloaded and installed Neuron, as described in Chapter 1.

Preparing for the simulation:

First read abut the theory of passive propagation of voltage changes down axons and dendrites.

Then load the simulation and click on the "Init & Run" button at the top right. The simulated axon or dendrite is 5000 mm in length and is impaled at one end by a current electrode. Voltage electrodes are placed 0.01, 0.25, 0.5 and 0.75 of the way along the axon (i.e. 50, 1250, 2500 and 3750 mm from the current electrode).

The various windows and graphs that you see are explained below.

To get some idea of how the simulation works, try moving the current electrode to the middle of the axon by clicking on the middle of the red line in Window D

The voltage distribution will now look like this. Make sure you understand why it has this shape before you move onto the rest of the Exercise.

Return the current electrode to the far left-hand end of the axon (or reload the program!!!)

Hypotheses to be tested and related observations to be made

Does the voltage change (depolarization - membrane potential during stimulation minus resting potential) produced by the injection of a steady level of current decline exponentially as the distance from the current electrode increases? Calculate the length constant of the axon. Explain any deviations from an exponential decline.
Increase the diameter of the axon or dendrite by a factor of two - to 18 mm - and the stimulating current to 23 nA (why do you have to increase the current as well?). Now re-calculate the length constant.
Reduce the diameter of the axon or dendrite by a factor of two - to 4.5 mm - and the stimulating current to 3 nA . Now re-calculate the length constant.
Do your calculations agree with the theory described below?

When you have loaded the simulation you should see Windows arranged as below. Click on the following letters: A B C D E F for a description of the function of each Window.
Return to Instructions

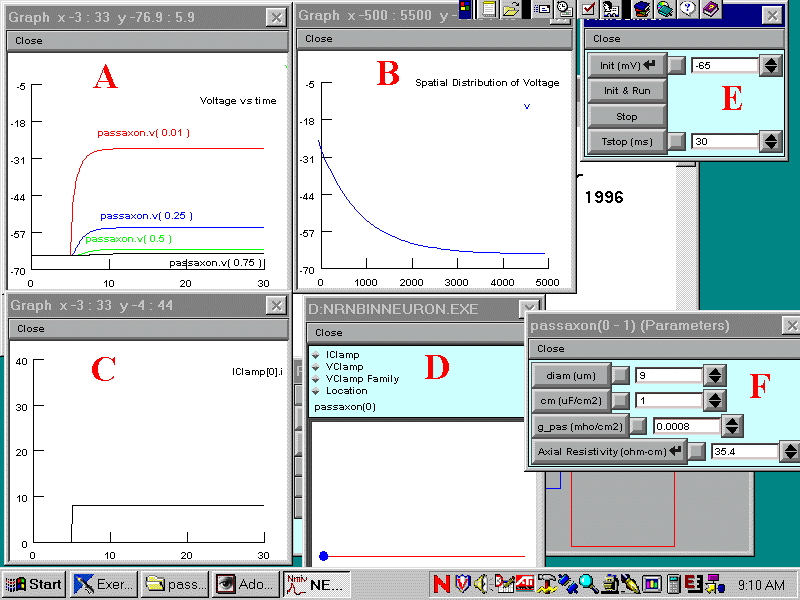
A. Graphs of membrane potential (mV) vs time (ms) recorded by voltage electrodes placed at the various positions along the axon or dendrite.
Return to letters

B. Graph of the calculated membrane potential (mV) as a function of the distance (mm) along the axon.

Return to letters

C. Graph of the current (nA) passed through the stimulating electrode.
Return to letters

D. Stimulation Parameter Window: As shown, this allows you to view and alter the position of the current electrode (blue dot) along the axon or dendrite (red line) click on various places along the red line to move the stimulating electrode.
Click on "IClamp" to view and alter the stimulating current.

You do not need to bother about the other buttons, which are not relevant to this simulation.

Return to letters

E. The Run/Control Box - click on Init & Run to run a simulation.
Return to letters

F. The parameters of the axon:

diam - the axon or dendrite diameter
cm - the specific membrane capacitance
g_pas - the passive membrane conductance
Axial resisistivity, R_a - the resistivity of the cytoplasm

Return to letters

Theory of passive propagation of voltage changes down axons and dendrites:

Because we are adding another dimension to the simulation - distance along nerves and dendrites - the simulations become more complex and you will need a little help with the theory.

The situation that is being simulated is shown below. The axon or dendrite is simulated as a cylinder of membrane which contains only passive, voltage - independent channels - it's much easier to think about this first without adding any voltage-dependent channels The axon is impaled by two electrodes. The current electrode is placed at one end of the axon or dendrite and a voltage electrode can be placed at varying distances along the dendrite or axon.

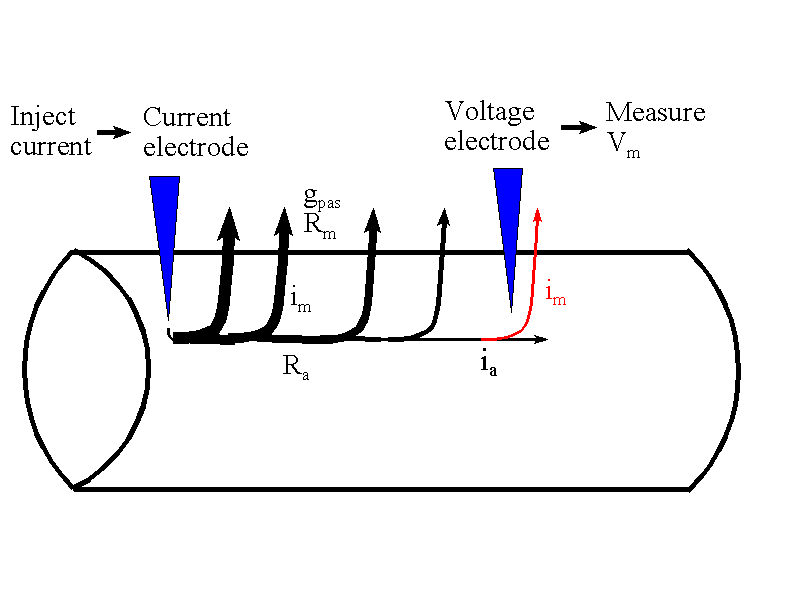
The injected current will flow out across the axonal membrane and create a depolarization of the membrane. However, not all of the current that is injected into the axon reaches the voltage electrode. As it travels down the axon some of it (the membrane current, i_mshown in black in the figure) leaks out through the membrane before it gets there. Only the membrane current that is shown in red, traveling across the axonal membrane close to the site of the voltage electrode, will result in a change in membrane potential at the site of the voltage electrode. Since this current (red line) is necessarily less than that which leaks out close to the current electrode (black lines), the voltage change produced by the stimulating current diminishes as the voltage electrode is placed further down the axon, away from the source of the stimulating current.
The rate at which the voltage signal diminishes depends on the ratio between the axial resistance per cm of axon (r_a) and the membrane resistance of a cm of axon, r_{m ,}(the latter in the case of our simulation being inversely proportional to the passive membrane conductance, 1/g_pas). This is because a high membrane resistance and low axial resistance will tend to keep current flowing down the axon and will increase the amount of current able to flow out of the membrane at the site of the voltage electrode.

For a steady, constant current, the exact form of the decline in the amplitude of the steady voltage change with distance from the electrode is exponential:

V_x=V_o.exp(-x/l)

where:
V_o is the voltage change produced by the stimulating current at the site of the current electrode
V_x is the voltage change produced by the stimulating current at the site of the voltageelectrode positioned at a distance, x, from the current electrode
l is the "space constant" which determines the rate at which V declines with x. Not surprisingly, l depends on the membrane and axial resistance and is equal to (r_m/r_a)^1/2

A large membrane resistance therefore results in a large l, which means that stimulating currents can produce large voltage changes over long distances down the axon.

What does all of this mean for the design of axons and dendrites?

As the diameter of an axon increases, axial resistance declines faster than membrane resistance (because axial resistance depends on the axonal cross sectional area - proportional to the square of the diameter - whereas membrane resistance is directly proportional to the diameter). Since l = (r_m/r_a)^1/2, this means that as axonal or dendritic diameter increases so does l. Therefore:

Voltage changes spread further by passive propagation down large diameter dendrites and axons

or put another way:

There is a limit as to how small a dendrite or axon can be made and still allow voltage changes to pass down it efficiently.

Return to Exercise