What have we learned?

• Basic data wrangling
• incl. regression coefs / sums of squares
• Probability theory
• distributions!
• Foundations of Inference
• hypothesis tests / confidence intervals
• Linear modeling / ANOVA
• (relies on pieces of everthing above!)

• Likelihoods and MLE’s
• … under the hood of GLM and lots more
• Generalizing linear models
• GLS (dependent data)
• random coefficients (LME’s)
• Bayesian Inference
• theory
• MCMC (with STAN)

Some Books

What we didn’t learn: More Advanced Regression

• GLMM
• easy!
• Additive models (GAM’s)
• leading to Generalized Linear Additive Mixed Models (GLAMM)
• Phylogenetic correlations
• easy! … just add the relationship matrix to `gls``
• Lasso / Spline bases / Ridge-regression
• fancy - but effective - stuff for solving some practical problems with outliers / funny distributions / non-linear responses.

What we didn’t learn: Multivariate Stats

For analyzing data with complex (multivariate) responses - e.g. multiple species presence / absence data.

• Multivariate regression
• MANOVA / MANCOVA
• Canonical-correlation analysis (CCA)
• Ordination / Dimension Reduction
• Principle Components (PCA)
• Factor Analysis
• Non-metric multidimensional scaling

What we didn’t learn: Machine Learning / Prediction

Actually: LOTS of overlap with topics we’ve discussed

(more than often acknowledged).

===========================================

Atlantic Cod Stomach Example

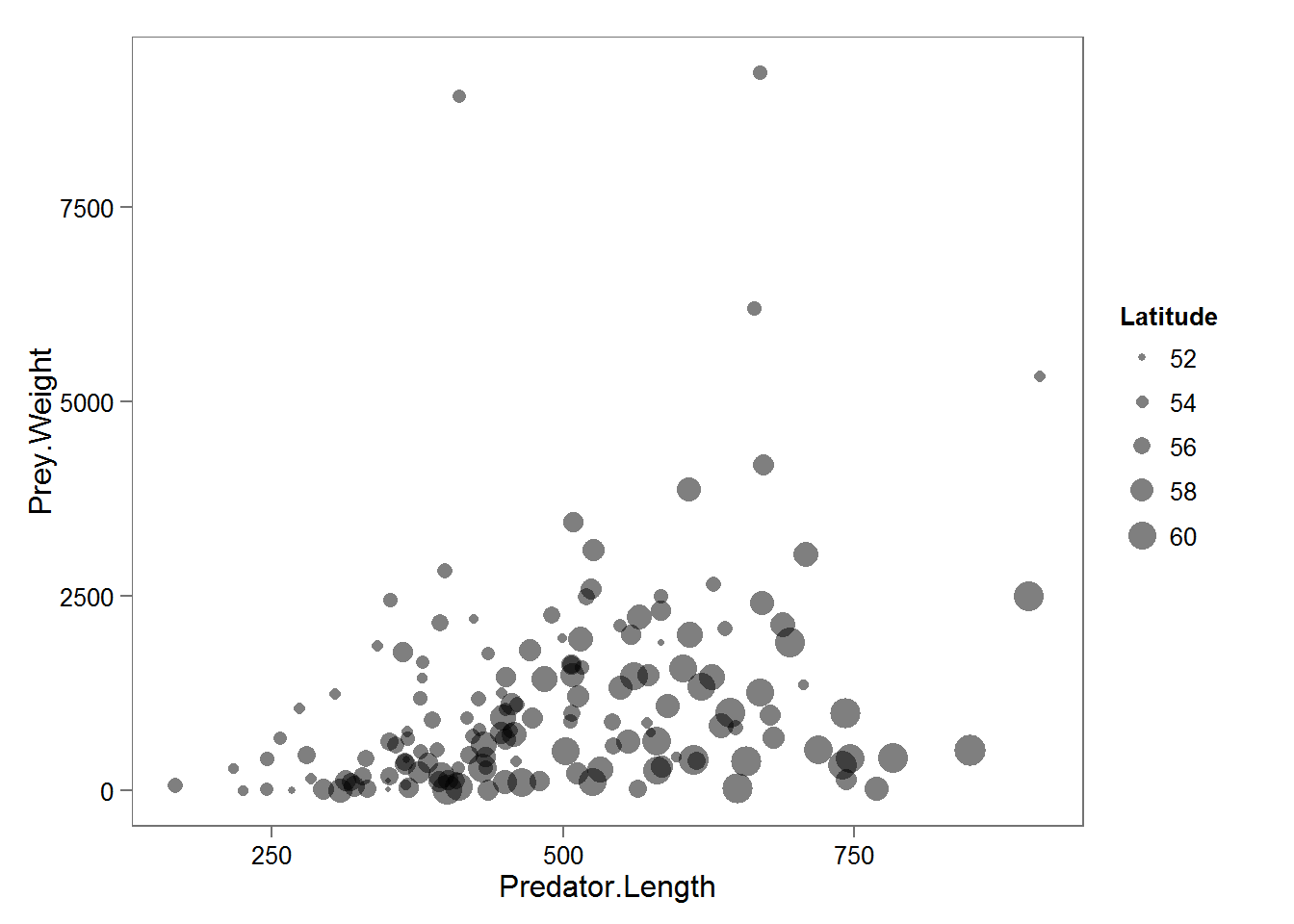
Model

\[W_{mean} = (\alpha_0 + \alpha_1 \text{Latitude})^\beta \times (L - L_{min})\] \[W_{obs} \sim \text{Exp}(mean = W_{mean})\]

where

• \(W\) is average stomach size
• \(\alpha\)’s are intercept / slope of regression against Latitude
• \(\beta\) is a scaling paramter
• \(L_min\) is the minimum size of a (captured) cod

Altantic Cod Stan Code

data {
  int n; //
  real Length[n]; // Predator length
  real WeightObs[n]; // Observed weight of stomach contents
  real Latitude[n]; // Latitudes at observations
}

parameters{
  real alpha0; // intercept & ...  
  real alpha1;  // ... slope of latitude dependence
  real Lmin;  // minimum length of predator for stomach contents
}

model{
  real WeightMean[n];  // mean weight
  // Priors 
  alpha0 ~ normal(0,1e3); 
  alpha1 ~ normal(0,1e3);
  Lmin ~ uniform(0, min(Length)); 
  // Likelihood 
  for(i in 1:n){
    WeightMean[i] <- (alpha0 + alpha1*Latitude[i]) * (Length[i]-Lmin);  
    WeightObs[i] ~ exponential(1/WeightMean[i]);  
  }
}

Atlantic Cod Stomach Example

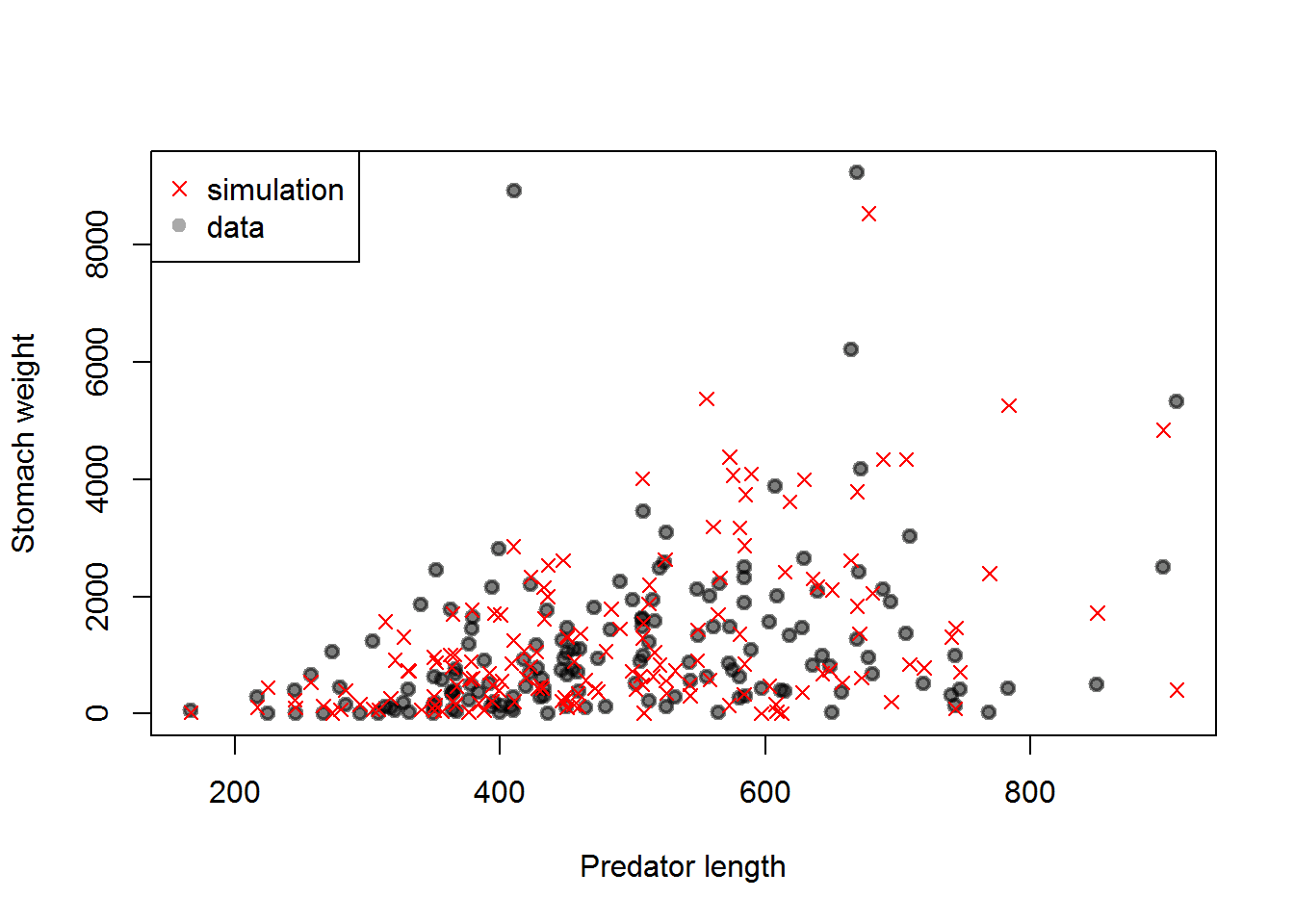
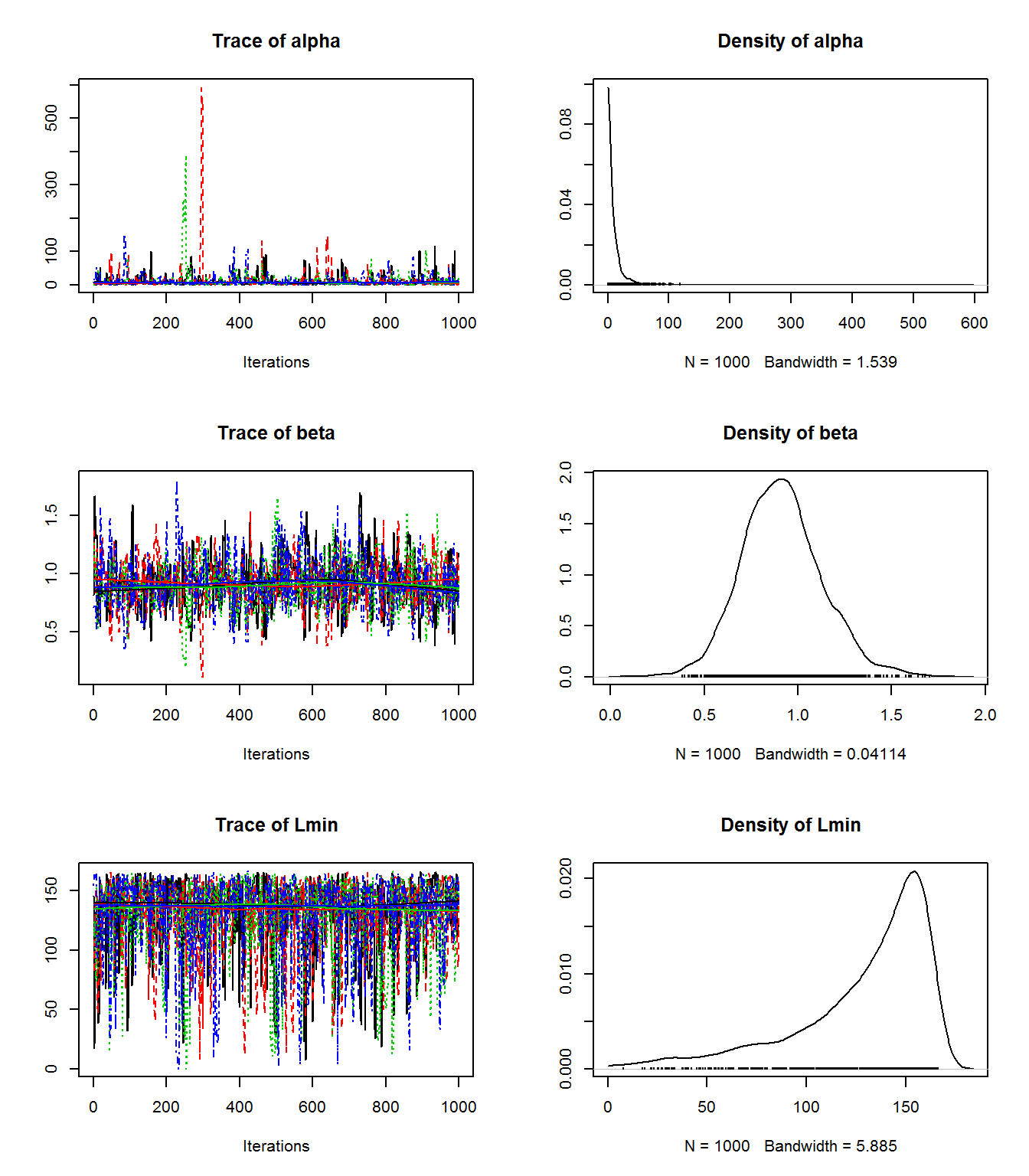
With that, Welcome to ….

The SECOND Annual Mega-Mini-Symposium on Data Analysis and Modeling in Ecology and Environmental Sciences and Genetics And Random Stuff

1. Opening Remarks and Welcome
2. Talks

1. First Speaker on First Topic

2. Second Speaker on Second Topic

3. Third Speaker on Third Topic

4. Fourth Speaker on Fourth Topic

etc…

---

Rubric

For each presentation, please write a brief sentence or two answering the following questions: