| Facilities | People | Research Projects | Educational Projects | Publications | Contact Director |
|---|
MECHANICAL
CHARACTERIZATION OF SHAPE MEMORY ALLOY COMPOSITES
FOR DESIGNING SMART STRUCTURES
| Hugh A. Bruck | Charles L. Moore |
|
Dept. of Mech. Engineering Clark School of Engineering University of Maryland College Park, MD |
|
Abstract
Actuators with large displacement ranges are being designed for smart structures by utilizing the unconventional mechanical behavior of Shape Memory Alloys (SMAs). This behavior is characterized by deformation recovery through thermally activated phase transformations. However, because of this deformation mechanism, conventional constitutive models cannot be employed to predict the mechanical behavior of SMAs. Appropriate constitutive models have been proposed, but their application can be computationally intensive. In this investigation, SMA wire-reinforced fiberglass composites are fabricated to determine the relationship between the mechanical response of the composite and the composition of SMA wire reinforcement. A modified linear Rule-of-Mixtures (ROM) formulation is proposed for predicting the mechanical behavior of the SMA composites. This simple, uniaxial constitutive model provides a reasonable prediction of SMA composite mechanical behavior, and is computationally efficient enough to use with Finite Element Analyses for designing smart structures that contain heterogeneous compositions.
I. INTRODUCTION
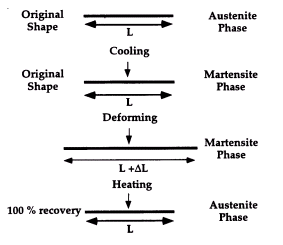
Structures that can actively adapt to changing environmental conditions are becoming a reality. These "smart" structures are being developed for a variety of military and commercial applications. For example, the DARPA/McDonnell Douglas Smart Materials Actuated Rotor Technology and DARPA/Boeing Smart Structures for Rotorcraft Control program are using smart materials to improve the performance of helicopter rotor blades [1-3]. These smart materials actively control the shape of the rotor blades through actuation of trailing edge trim tabs, edge flaps, and passive torque tubes in order to reduce vibrations and improve lift. When large changes in shape are controlled, actuators fabricated with Shape Memory Alloys (SMAs) are used. These active structures take advantage of the unique thermomechanical behavior of SMAs, known as the Shape Memory Effect (Figure 1), which results in large, recoverable deformations when the alloys are heated. The resulting power ratios are very high, which enable SMA actuated systems to be fabricated at much smaller size scales than conventional hydraulic or mechanical actuation systems. The SMA devices used in these structures are constructed from wires and tubes that are "trained" to actuate the structure. The high power ratio of SMAs has been especially beneficial in designing and developing actuators for controlling robotic hands [4,5].

Figure 1. Schematic illustrating the Shape Memory Effect
SMAs possess many other characteristics that are desirable for actuation applications. For example, actuators can be fabricated from a single SMA element, resulting in simpler and more reliable devices. SMA actuators made from Ni-Ti are highly corrosion resistant, and with no additional vibrating parts they are silent, clean, and relatively unaffected by the operating environment. Smooth movements can also be achieved with these actuators, making them ideally suited for spacecraft.
New opportunities for expanding the use of SMAs in the design of smart structure is being realized by embedding NiTi wires into polymers, elastomers, and fiber-reinforced/epoxy composites [6, 7]. The embedded wires can be used to activate flexible materials, like polymers and elastomers, or improve the toughness and buckling resistance of brittle materials, like fiber-reinforced/epoxy composites [8]. In developing these materials, research efforts are focussing on overcoming technical barriers such as: increasing actuator stroke, building reliable smart material data bases, developing robust distributed parameter control strategies, and mathematically modeling smart systems [9].
It is the intent of this study to investigate the design of smarter, more reliable SMA actuated devices using wire-reinforced composites with varying volume fractions. The development of a constitutive model for describing the mechanical behavior of SMA wire reinforced materials will be studied for varying volume fractions of wire reinforcement. The information obtained will be critical in determining the potential of these materials for activating structures, as well as the suitability of SMA composite models for use with Finite Element Analyses (FEA) to design smart structures.
II. Mechanical Behavior of Shape Memory Alloys
The mechanical behavior of SMAs is characterized by phase transformations that are activated through changes in temperature and/or loading. These transformation lead to very large recoverable deformations, otherwise known as the Shape Memory Effect or pseudoelasticity (Figure 2). Three-dimensional T-s-e diagrams are often constructed to describe this behavior for design purposes [10]. However, these diagrams can only be used to predict the cooling behavior of isobarically loaded structures, therefore they may not be useful in predicting their behavior under complex loading and temperature paths.
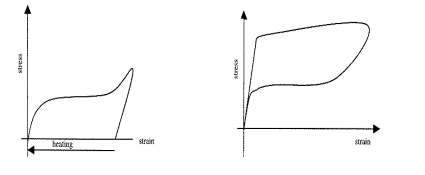
| (a) | (b) |
Figure 2. (a) Shape Memory Effect at T< As and (b) Pseudoelasticity at T>Af for a SMA.
To account for the complex thermomechanical constitutive behavior of SMAs, some general models have been proposed. Tanaka proposed the following model based on the second law of thermodynamics expressed in terms of the Helmholtz free energy [11]:
| (1) | |
| (2) | |
| (3) | |
| (4) |
where, aA, aM, bA, and bM are material constants. In this model, strain, temperature, and martensite volume fraction were used as state variables, with the martensite volume fraction expressed as an exponential function of temperature.
Liang and Rogers proposed a modified rate form of Tanaka's constitutive expression, using a cosine description of volume fraction to eliminate singularities at 100% austenite and 100% martensite phases [12]. A final modification to Tanaka's model was proposed by Brinson, where the coefficients of the constitutive equation are assumed to be non-constant and the martensite volume fraction is equal to the sum of stress-induced and temperature-induced martensite [13]. An alternative model proposed by Boyd and Lagoudis uses Gibbs free energy rather than the Helmholtz free energy [14]. Experimental analaysis by Epps and Chopra concluded that all of the models provide reasonable predictions, although the Brinson model was the most accurate [15]. DeGiorgi and Saleem also compared the computational efficiency of all of the models except Brinson's in a FEA for predicting the deformations of a torsion tube, concluding that all models were adequate with only the Liang and Rogers model being inefficient [16].
III. SMA Composites
While comparisons of constitutive models for SMAs have been undertaken for designing smart structures using FEA, similar comparative analyses have not been performed for SMA composites. Micromechanical models have been proposed to quantify the effects of the shape and volume fraction of reinforcement on the thermomechanical behavior of SMA composites using Mori-Tanaka's mean field and Eshelby's equivalent inclusion methods [17-19]. However, because these models rely on the constitutive models for homogeneous SMAs, they can become far more computationally inefficient to use. Computational efficiency is especially important when considering the design of smart structures using SMA composites. Therefore, the use of simple constitutive models is imperative
Bruck and Rabin investigated the use of simple rule-of-mixtures (ROM) formulations for describing the thermomechanical behavior of metal-ceramic composites [20,21]. In this approach, the deformation behavior at terminal compositions is used as inputs to ROM formulations to predict material behavior at intermediate compositions. The use of ROM formulations, although not as accurate as mean field or inclusion models, was determined to be adequate and greatly simplified Finite Element Analysis. Therefore, the use of ROM formulations for SMA composites of varying composition may also prove to be reasonably accurate and computationally efficient.
IV. Fabrication and Testing of SMA Composites
Model SMA composite specimens were fabricated by embedding untrained NiTi wires with diameters of 15 mils into a woven fiberglass matrix (Figure 3). This matrix was then infiltrated with a compliant adhesive to increase the flexibility of the composite and improve the toughness of the matrix. The composite was then pressed between platens and cured at 80 C for 1 hour. Specimens contained 3, 6, and 9 embedded wires resulting in volume fractions of 0.081, 0.125, and 0.166. A dog-bone geometry was used for tensile testing, with a gage length of 1.5 inches and a width of 0.25 inches. Specimens were tested in an Instron screw-driven load frame at a displacement rate of 0.05 cm/min, resulting in an equivalent strain rate of 0.0002/sec. The specimens were aligned so that the direction of the fibers coincided with the loading direction for the specimen.

Figure 3. Dog-bone
fiber glass composite specimens with
0, 0.081, 0.125 and 0.166 volume fraction
of NiTi wire.
V. Experimental Results and Discussion
Experimental results from testing 3, 6 and 9 wire SMA composites and plain fiberglass specimens can be seen in Figure 4. The mechanical behavior of the composites was reasonably reproducible (Figure 5). It is immediately evident that the composites exhibit greater ductility than either the composite or fiberglass specimens. By increasing ductility, composites provide the basis for fabricating more flexible smart structures with larger actuation strokes. However, this enhanced ductility is obtained at the expense of strength. While the ductility of the composites is 100% greater than the wire and nearly 600% greater than the fiberglass, the ultimate strength is almost identical to the fiberglass composite and about 20% of the wire. The mechanical behavior of the composites exhibited slight variations with composition, with the strength and ductility increasing in conjunction with the wire reinforcement.
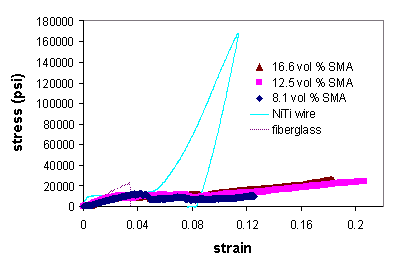
Figure
4. Uniaxial tension data for SMA composites along with NiTi wire and plain fiberglass.
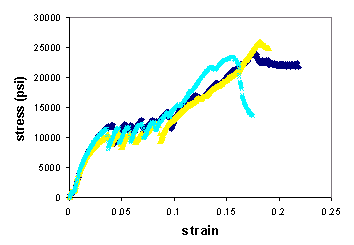
Figure 5. Uniaxial tension data for
3 identical SMA composite specimens.
Because of their increased ductility and reduced strength, the SMA composites can not be modeled using traditional ROM formulations. Therefore, it was proposed to modify the linear ROM formulation to predict their mechanical performance. The traditional linear ROM constitutive model for a fiber reinforced composite loaded in the direction of the fibers is given as follows:
| (5) |
where scomposite is the stress in the composite, ecomposite is the strain in the composite, Vmatrix is the volume fraction of the matrix, smatrix is the stress in the matrix, Vfiber is the volume fraction of the fiber and sfiber is the stress in the fiber. In equation (5), the thermomechanical constitutive models in Section II can be used to describe the stress in the NiTi wires. For a fiberglass composite matrix, the stress in the matrix will be directly proportional to the stiffness of the matrix.
During testing of the composites, damage in the fiberglass matrix and pullout of the NiTi wire was observed. Therefore, it was proposed to modify the linear ROM formulation by using an exponential decay of stress in the fiberglass matrix and strain transmitted to the NiTi wire as follows:
| (6) | |
| (7) |
where Ematrix is the modulus of elasticity of the fiberglass matrix, ewire is the strain in the wire, and a and b are constants determined by a data fit. The results from this fit can be seen in Figure 6 for a = 0.045 and b=5. These values provided reasonable fits to the data for all of the compositions, indicating that the deterioration in matrix strength and strain transmitted to the wires is independent of the volume fraction over the range of compositions tested. This simple constitutive model provides a computationally efficient description of material behavior to use with Finite Element Analyses for designing smart structures.
Upon unloading the 0.166 volume fraction SMA composite specimens after a 20% elongation, 10% of the applied strain was recovered. This is consistent with the recovery predicted by the modified linear ROM formulation seen in Figure 6. Because the deformation mechanisms that are present during loading (e.g., phase transformations, damage evolution in matrix) are not active during unloading, the correlation of measured and predicted recovery strain further verifies the validity of the assumptions made in equations (6) and (7).
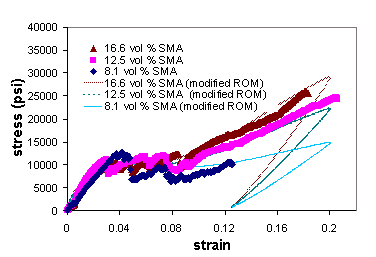
Figure 6. Modified linear ROM fits to SMA composite
data.
VI. Conclusions
Model SMA composites were prepared by embedding 0.081, 0.125, and 0.166 volume fraction of NiTi wire in fiberglass. Composite specsimens were loaded in the direction of the wire reinforcement to determine the variation of their tensile behavior with the volume fraction of wire reinforcement. The composites were found to be twice a ductile as the NiTi wires and seven times as ductile as fiberglass, but possessed ultimate strengths that were almost identical to the fiberglass. Their mechanical response exhibited slight variations over the range of compositions tested, with the strength and ductility increasing as the volume fraction of wire reinforcement was increased. To predict this performance, a modified linear rule-of-mixtures formulation was proposed using an exponential decay of stress in the fiberglass matrix and strain transmitted to the wire reinforcement. This simple constitutive model reasonably predicted the mechanical behavior of the composites using constants that were composition invariant, providing a computationally efficient description of material behavior to use with Finite Element Analyses for designing smart structures.
Acknowledgments
The authors would like to thank Prof. Inderjit Chopra of the Department of Aerospace Engineering for his support.
References
[1] Epps, J.J. and Chopra, I., "Shape Memory Alloy Actuators for In-flight Tracking of Helicopter Rotor Blades", Proc. of the 5th Ann. SPIE Int. Symp. on Smart Struct. and Matls., San Diego, CA (1998).
[2] Liang, C. and Davidson, F., "Applications for Torsional Shape Memory Alloy Actuators for Active Rotor Blade Control - Opportunities and Limitations", Proc. of the SPIE Smart Struct. and Matls. Conf., San Diego, CA (1996).
[3] Giurgiutiu, V., Rogers, C.A., and Zuidervaart, J., "Incrementally Adjustable Rotor-Blade Tracking Tab Using SMA Composites", Proc. of the 38th Struct., Struct. Dyn. and Matls. Conf. and Adapt. Struct. For., Kissimmee, FL (1997).
[4] Chaudhuri, P. and Fredericksen, D.H., "Robot Hand with Shape Memory Musculature", IBM Technical Disclosure Bulletin, 28, 302-3 (1985).
[5] Nakano, Y., Fujie M., and Hosada, Y., "Hitachi's Robot Hand", Robotics Age, 18-20 (1984).
[6] Wei, Z.G., Tang, C.Y., and Lee, W.B., "Design and Fabrication of Intelligent Composites Based on Shape Memory Alloys", J. of Matls. Proc. Tech., 69, 68-74 (1997).
[7] Wei, Z.G., Sandstrom, R., and Miyazaki, S., "Review: Shape Memory Materials and Hybrid Composites for Smart Systems. Part II. Shape-memory hybrid composites", J. of Matls. Sci., 33, 3763-3783 (1998).
[8] Liang, C., Rogers, C.A., and Malafeew, E., "Smart Structures and Materials", AD-Vol. 24/AMD-Vol.123, ed. by G.K. Haritos, ASME, New York, 97 (1991).
[9] Chopra, I., "State-of-the-Art of Smart Structures and Integrated Systems", Proc. of the SPIE Smart Struct. and Matls. Conf., San Diego, CA (1996).
[10] Reynaerts, D. and Van Brussel, H., "Design Aspects of Shape Memory Actuators", Mechatronics, 8, 635-656 (1998).
[11] Tanaka, K., "A Thermomechanical Sketch of the Shape Memory Effect: One-dimensional Tensile Behavior", Res. Mechanica, 18, 251-263 (1986).
[12]&nsbp; Liang, C. and Rogers, C.A., "One-Dimensional Thermomechanical Constitutive Relations for Shape Memory Material, J. of Int. Matls. and Struct., 1, 207-234 (1990).
[13] Brinson, L.C., "One-Dimensional Constitutive Behavior of Shape Memory Alloys: Thermomechanical Derivation with Non-Constant Material Properties", J. of Int. Matl. Sys. and Struct., 4, 229-242 (1993).
[14] Boyd, J.G. and Lagoudas, D.C.," A Thermodynamic Constitutive Model for the Shape Memory Materials. Part I. The Monolithic Shape Memory Alloys", Int. J. of Plast., 12, 805-842 (1996).
[15] Epps, J.J. and Chopra, I., "Comparative Evaluation of Shape Memory Alloy Constitutive Models with Test Data", Proc.s of the 38th AIAA Struct., Struct. Dyn. and Matls. Conf. and Adaptive Structures Forum, Kissimmee, FL (1997).
[16] DeGiorgi, V.G. and Saleem, H., "A Comparison of A Few Shape Memory Alloy Constitutive Models", Proc. of the 6th SPIE Int. Symp. on Smart Matls. and Struct., Newport Beach, CA (1999).
[17] Song, G.Q., Sun, Q.P., and Cherkaoui, M., "Role of Microstructure in the Thermomechanical Behavior of SMA Composites", J. of Eng. Matls. and Tech.-Trans. of the ASME, 121, 86-92 (1999).
[18] Yang, Q.S., "Thermomechanical properties of smart composites", Acta Mechanica Solida Sinica, 9, 357-363 (1996).
[19] Boyd, J.G. and Lagoudas, D.C.," A Thermodynamic Constitutive Model for the Shape Memory Materials. Part 2. the SMA Composite Material", Int. J. of Plast., 12, 843-873 (1996).
[20] Bruck, H.A. and Rabin, B.H., “An Evaluation of Rule-of-Mixtures Predictions of Thermal Expansion in Powder Processed Ni-Al2O3 Composites”, to appear in J. of the Amer. Cer. Soc.
[21] Bruck, H.A. and Rabin, B.H., ”Evaluating Microstructural and Damage Effects in Rule-of Mixtures Predictions of the Mechanical Properties of Ni-Al2O3 Composites for Use in Modeling Functionally Graded Materials”, Journal of Materials Science, 34, 2241-2251 (1999)