Homework Assignment 2


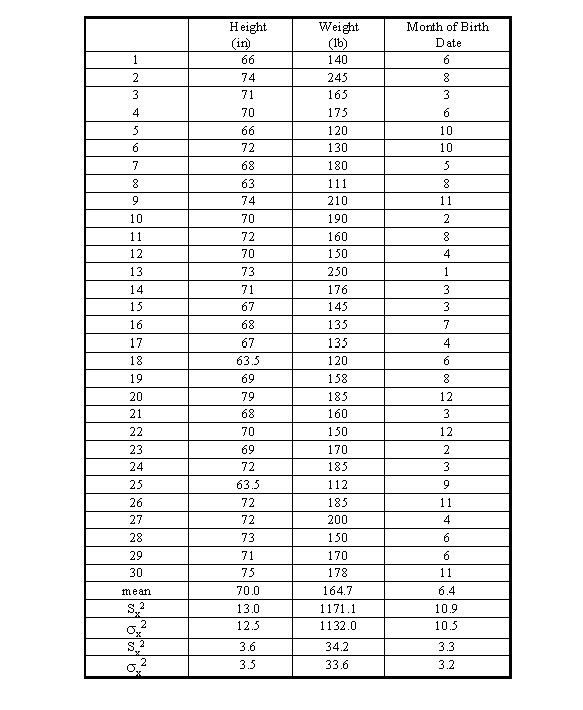
2.4.1 Using the three sets of data about the height, weight, the month of the birth-date of a group of specific students in a specific class, do the following:

(1) Calculate the mean, variance, and standard deviation for each data set.

(2) Construct three histograms for the three data sets.

(3) By examining the constructed histograms, interpret the numerical values of the mean and standard deviation you have obtained.

It is suggested that you use a computer to do problem 1. Any spread sheet program will be useful.


(1) Calculate the mean, variance, and standard deviation for each data set.




(2) Construct three histograms for the three data sets









2 Use the following formulas to calculate Babe Ruth's 15 yearly home run data





3 Calculate the mean, variance, and standard deviation using the following formulas:

(1)


(2)




4. The outcome from throwing a single, true, six-sided die is a random variable. Its mean is equal to 3.50, and the standard deviation is equal to 1.71. Assume Y=(X1-X2)/2 where X1 and X2 represent two dice. Based on the principle of linear operator, calculate and






5. Assume that Z represents a normal random variable with mean 0 and standard deviation 1.

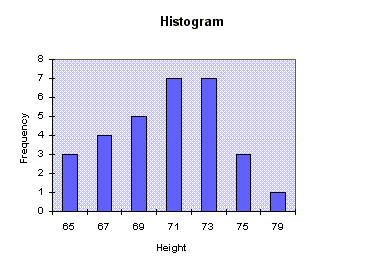
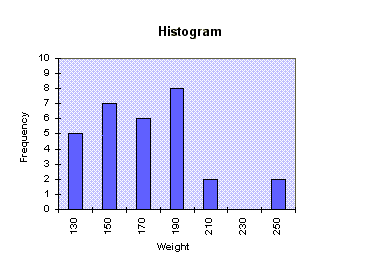
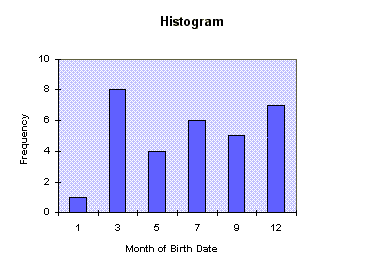
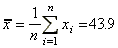
(1) Determine P(Z>1.96); (2) Determine P(-2<Z<2); (3) Determine P(0<Z<3).


(1) Determine P(Z>1.96)

P(Z>1.96)=1-P(Z<1.96)=1-0.9750=0.0250

(2) Determine P(-2<Z<2)

P(-2<Z<2)=2P(0<Z<2)=2(P(Z<2)-P(Z<0)=2*(0.9772-0.5)=0.9544

(3) Determine P(0<Z<3)

P(0<Z<3)=P(Z<3)-P(0<Z)=0.9987-0.5=0.4987



6. The SAT scores for the XYZ university admission are normally distributed with mean 1055 and standard deviation 75. What fraction of the SAT scores lie between 1100 and 1200?

P(1100<X<1200)=P(X<1200)-P(X<1100)


P(1100<X<1200)=P(0.6<Z<1.93)=0.9732-0.7257=0.2475