Assignment 2 Solutions
Problem 1)
True Length = SQRT of (diff x^2 + diff y^2 + diff z^2)
| Column |
Length |
Beam |
Length |
| AF |
4.00 |
AB |
13.38 (root of 11^2+7^2+3^2) |
| BG |
7.00 |
BC |
3.32 (root of 3^2+1^2+1^2) |
| CH |
8.00 |
CD |
11.58 (root of 10^2+5^2+3^2) |
| DE |
5.00 |
AD |
3.74 (root of 2^2+3^2+1^2) |
The areas are easiest solved using vector cross-products.
Divide the top into two triangles.
The problem becomes basic vector manipulation. An area of a
triangle is one half the area of the parallelogram represented by
two vectors.
( i.e. 1/2 (vector1 x vector2) )
Given the three points D(0,3,5) A(2,0,4) C(10,8,8)
Vector DA = (2-0,0-3,4-5) = (2,-3,-1)
Vector DC = (10-0,8-3,8-5) = (10,5,3)
The area is equal to the numerical value of 1/2 (DA x DC)
| 1/2 |
| i
| 2
| 10
|
j
-3
5
|
k |
-1 |
3 |
|
= 1/2 |-4i -16j + 40k| = 21.6333 |
Vector AB = (11,7,3)
Vector AC = (8,8,4) then, 1/2 (AB x AC) = 18.9737
Area of ABCD = Area of DAC + Area of ABC
Area of DAC = 21.6333 ft^2
Area of ABC = 18.9737 ft^2
Area of ABCD = 40.6070 ft^2
Thickness of ABCD = 0.020833 ft.
Volume of ABCD = 0.845964 ft^3
Density of Steel = 490 lb/ft^3 for ASTM A36 Structural Carbon
Steel, Rolled
Total Weight of Top Sheet = 414.5228 lb.
Problem 2)
Again, this problem is solved quickly using vectors.
% Find relative Z values
Az = 20*tan(60) = 34.6410
Cz = 30*tan(30) = 17.3205
% Position of Vertices
B = [0 0 0]
A = [0 -20 -Az] = [0 -20 -34.6410]
C = [-30 0 -Cz] = [-30 0 -17.3205]
% Create vectors
AB = B-A = [0 20 34.6410]
AC = C-A = [-30 20 17.3205]
CA = A-C = [30 -20 -17.3205]
CB = B-C = [30 0 17.3205]
% Find true length of AC (root of x^2+y^2+z^2)
X = norm(AC) = 40.00
% Find vector angles
% ( angle = acos(dot product of two / multiplying norms of two )
AngA = acos(dot(AB,AC)/(norm(AB)*norm(AC))) = 51.3278
AngB = acos(dot(AB,CB)/(norm(AB)*norm(CB))) = 67.9757
AngC = acos(dot(CA,CB)/(norm(CA)*norm(CB))) = 64.3410
Problem 3)
This is a problem of Descriptive Geometry.
View H represents the Top View
View F represents the Front View
The revolution method involves rotating a line, or part, so that the edge you are trying to measure
is at a right angle to you as the viewer. Only then is its True Length (TL) shown.
Slope can ONLY be determined in the front views (where there exists a horizontal plane) and only
when an entity of true length is being referenced in the same view.
FIGURE 1
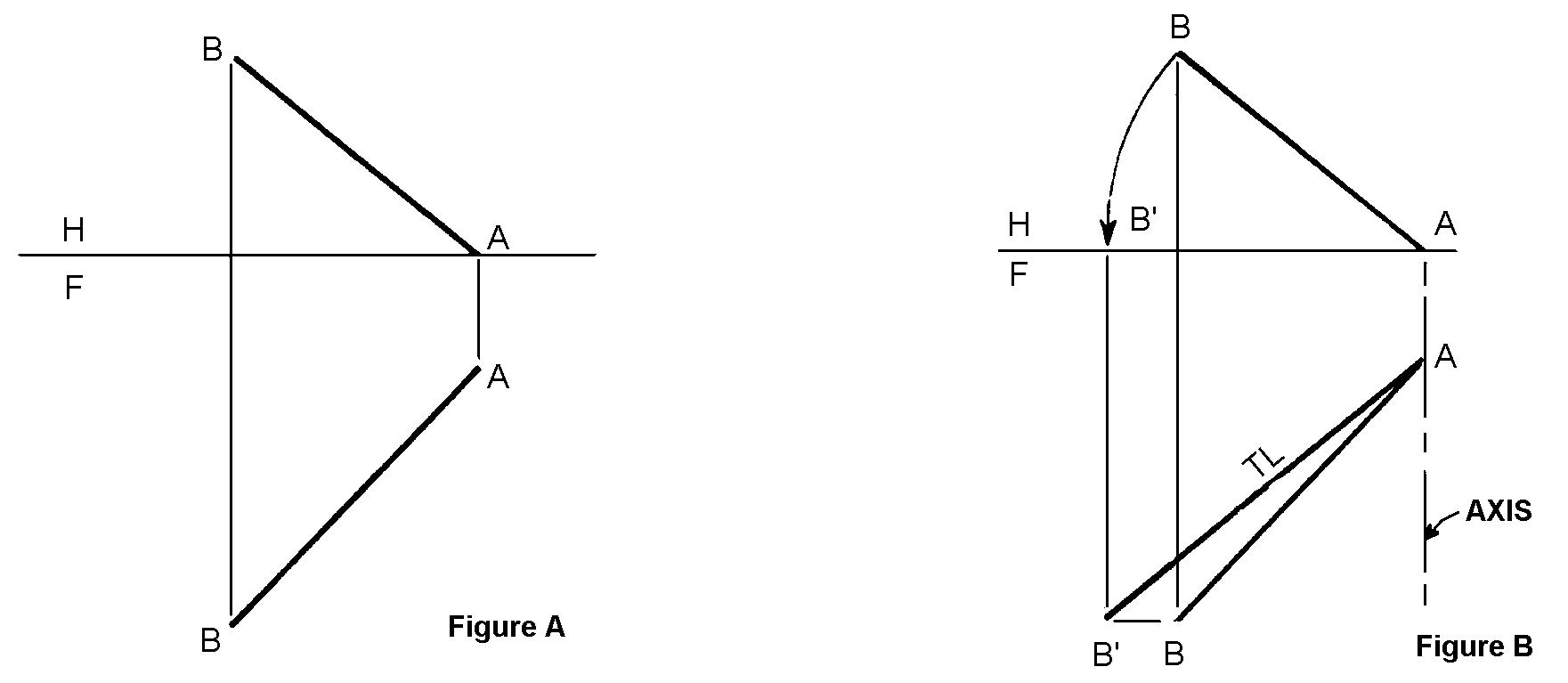
A line projects true length into any view when it appears in an adjacent view parallel to the image
plane of the first view. An oblique line can be revolved about an axis through a point of the line
until the line is parallel to an image plane only when the axis appears as a point. Figure A shows
the top and front views of the given line AB, whose true length is to be found. A vertical axis
through point A in the front view will project as a point in the top view, as shown in Figure B.
Revolve point B in the top view about the axis through point A until line AB is parallel to the
image plane H-F. Project the revolved position of point B, labeled B', to the front view to where
it intersects a horizontal projection from point B in the front view. Connect A to B' to measure
the true length of line AB.
FIGURE 2
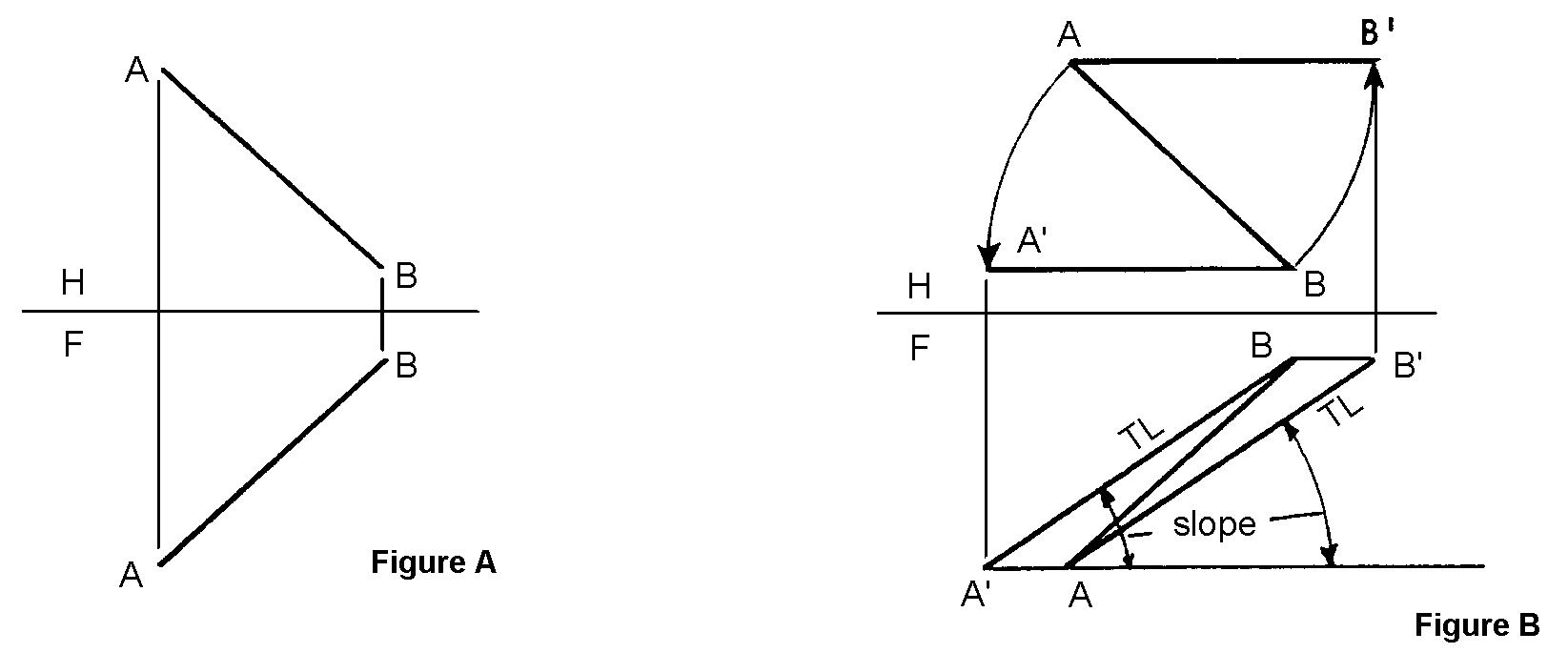
Figure A shows the front and top views of the given line AB, whose true slope is to be found.
The true slope of a line can be measured in a view in which the line appears true length. As
shown in Figure B, the axis about which line Ab is to be revolved can be through either point A or
point B. If the axis is chosen through point A, revolve point B to B' where line AB' is parallel to
the reference plane H-F. Project B' to the front view, where line AB' appears true length. The
required slope is the angle between line AB' and a horizontal line. If the axis is chosen through
point B, revolve point A to A', where line A'B is parallel also to plane H-F. Project A' to the front
view, where line A'B is true length. The required slope is then measured as the angle between line
A'B and the horizontal line. Note than A'B and AB' are parallel to each other, verifying the fact
that their slopes must be equal since they represent the same line.

