ENME 414 Computer Aided Design

Homework Assignment 2 - Descriptive Geometry

Due Wednesday, February 18, 1997

Statement: Descriptive geometry represents the study of identifying the relationships between the geometric features in three-dimensional space and the basic geometric elements, such as points, lines, and planes in two-dimensional space. Descriptive geometry serves as the foundation to formulate the framework and algorithms in the CAD software development. Thanks to the rapid development of information technology, the subject of descriptive geometry no longer plays a critical role in learning engineering graphics. However, it is still important to understand of the two-way conversions from a 3D space to a 2D space, and vice versa.


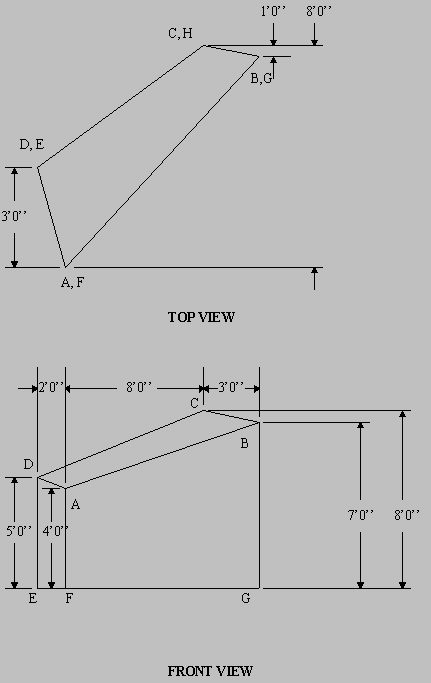
  1. A storage bin has been designed. It is shown in the following figure. Before constructing the bin, raw material has to be prepared. As illustrated, six cylindrical columns made of steel, AH, BI, CJ, DK, EL, and FG, are needed. Six rectangular beams made of steel, AB, BC, CD, DE, EF, and AG, are needed. The top surface, ABCDEF, should be covered by a sheet of steel.
    2. (1). Use a spreadsheet to prepare a list indicating the true length of each of the six columns and beams.
    (2). Calculate the weight of the top cover sheet, ABCDEF. Assume that the thickness of the steel sheet is ¼."

  2. Two tubes AB and BC are to be connected by a third tube AC, thus completing the circulation of air among the three locations, A, B and C. Note that location B is at the top of a hill. The top of the hill is 20 ft north of A and 30 ft east of C. The slopes of AB and BC are 60 degrees and 30 degrees, respectively.
    3. 1. Draw the front, top, and right side views of the design configuration.
    2. Find the true length of the third tube AC.
    3. Find the true size of the angle for the special fitting.
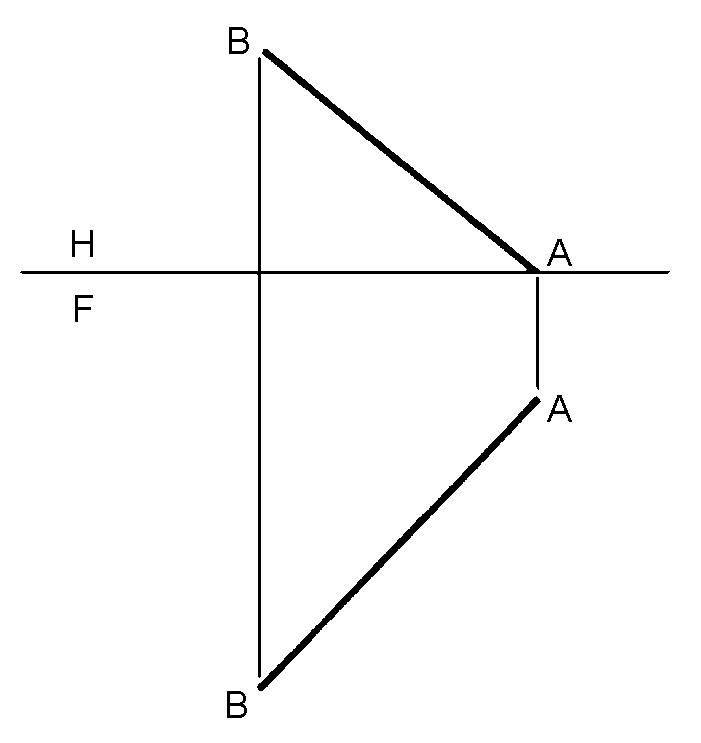
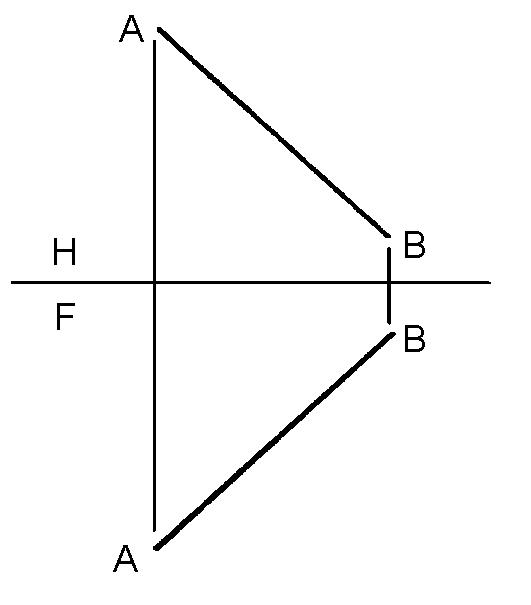
  3. The revolution method in descriptive geometry assumes that the observer is considered to occupy a fixed position while the object is rotated into different positions to obtain different views. Certain problems can be more easily solved by revolution. The following problems to calculate the true length and slope of lines should be solved using the revolution method.
    4. 1. In Figure 1, find the true length of a given line AB.
    2. In Figure 2, find the true slope of a given line AB.

Figure 1

Figure 2