Wigner's Nobel Prize
- Click here for an article from the ArXiv.
- Click here for the same article with sharper images.
- Since Wigner received his Nobel prize in 1963, many people invented many different
programs carrying Wigner's name, in order to elevate themselves.

Photo with Toll and Wigner (1986).
Faculty photo of 1963. I am
the youngest man in this photo.
- Many distinguished people, including Louis Michel and Arthur Wightman, accused me
of taking advantage of Wigner's name. They seem to be right. My plan to approach
Wigner was to study his papers and find further applications to physics. At one of
the campus meetings in 1982, I told about this plan to John S. Toll who was the
chancellor of the University of Maryland at that time. Toll was very happy to hear
about my plan, and told me Wigner would like my method best. Toll was right.
Toll was kind enough to invite me and Wigner at the Chancellor's residence when Wigner came to Maryland in 1986, and we had this photo.
John S. Toll was John A. Wheeler's student at Princeton, and came to the University of Maryland in 1953 to build the physics department. He hired me as an assistant professor in 1962 one year after I got my degree in 1961. He always gave me correct advices whenever I needed them. When he invited Paul A. M. Dirac to Maryland in September of 1962 for a week, Toll assigned me as Dirac's servant. Click here for an interesting story.
- Wigner published many papers. What is the best way to reach his heart and mind?
He was awarded the Nobel Prize in Physics in 1963 for
his contributions to the theory of the atomic nucleus and the elementary particles, particularly through the discovery and application of fundamental symmetry principles.
Wigner was of course happy to get the prize. Here is a photo of Wigner at the Nobel dinner in December of 1963. He went there with his former high-school class mate. Wigner had one daughter and his friend had three daughters. Thus, there are four young ladies in this photo. You will be interested to hear that I have photos with three of those four young ladies.

Wigner was very happy to get the prize. However, he was not 100% happy, because the prize citation did not mention the contribution he made in his 1939 paper on the Lorentz group. The prize committee did not know the physical content of this paper. Should we blame them? Yes and No.
We can rephrase the question in the following way. Did Wigner deserve the prize for this paper alone? Some people say Yes, and some others say No. Both seemed to be right in 1963. How about Wigner? Wigner thought Yes, but he was eager to provide a stronger YES.
In his 1939 paper, Wigner provided the Lorentz covariant interpretation of the spin of a massive particle, by considering the subgroups of the Lorentz group whose transformations leave the momentum of a given particle invariant. He called them "little groups."
- If a particle is at rest, there is a Lorentz frame in which it is at rest.
In this frame, the momentum is invariant under three-dimensional rotations.
Thus, the little group is O(3), leading to the concept of the spin. If
the particle moves, the little group is a Lorentz-boosted O(3) still with
three generators.

Wigner did not get the prize for his 1939 paper because his did not provide the physics of this matrix. - For a massless particle, there are no Lorentz frames where it is at
rest. This particle can be rotated around the momentum, leading to
the concept of helicity. In addition, Wigner found two additional
transformations which leave this light-like momentum invariant.
However, he could not provide the physics of those transformations.
Click here for an illustration.
For this reason, Wigner did not get the prize. It is safe to say.
- Wigner however was clever enough to give a group theoretical interpretation
to these matrices. The Lorentz group has six generators consisting of
three rotation and three boost generators. If we use the notations
Ji and Ki for those generators respectively, the rotation generators
satisfy a closed set of commutation relations. Thus the rotation group is
a subgroup of the Lorentz group as we noted before for the massive particle.
In addition, Wigner constructed the three generators
-
J3 ,
N1 = K1 - J2 ,
N2 = K2 + J1 .These generators satisfy the closed set of commutation relations
[ N1 , N2 ] = 0 ,
[ J3 , N1 ] = i N2 ,
[ J3 , N2 ] = - i N1 .Wigner, in his 1939 paper , noted that this set of commutation relations is identical to that for the E(2) group or the two-dimensional Euclidian group with with one rotational and two-translational degrees of freedom.
- In 1987, I and Wigner published
a paper showing that there is the
cylindrical group isomorphic to the E(2) group and thus to the
little group for massless particles. It is a cylindrical group
with one rotational and one translational degrees of freedom. This
group can explain the helicity and the gauge degrees of freedom, as
illustrated in this figure.
Click here detailed calculations.
This 1987 paper gives the physical interpretation of the E(2)-like little group introduced by Wigner in 1937, and published 1939. It took the physics world fifty years to complete the job of introducing the little group as the fundamental group governing the internal space-time symmetries of massive and massless particles.
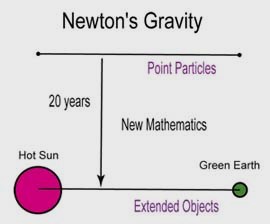
Newton initially formulated his gravity law between the sun and earth assuming that they are point particles. It took him 20 years to work out the same law for extended objects. 
- Is this the end of Wignerism? No. It is only a beginning of a new
phase of physics. Isaac Newton formulated his gravity law between
the sun and earth assuming that they are point particles. It took
him 20 years to complete the law for extended objects. He had to
develop a new mathematics, known today as integral calculus.
Likewise, Bohr and Einstein met occasionally to talk about physics. Bohr was worrying about the electron orbit in the hydrogen atom. Einstein was worrying about how things look to moving observers. Did they talk about how the electron orbit looks to a moving observer? If they did, we do not know about it. Wigner's little groups, defined for the Lorentz-covariant world, force us to back to this Bohr-Einstein issue. Click here for a story. The hydrogen orbit is an issue of the internal space-time symmetry.
Indeed, Wigner's 1939 paper leads us to examine whether Einstein's Lorentz covariance holds inside relativistic extended particles. On this issue, I also published a paper with Wigner in 1990. By that time, Wigner became very weak physically. I thus had to do most of the work for that paper. Click here for the paper. If the paper is boring to read, you can go to this webpage with colorful illustrations.
- If a particle is at rest, there is a Lorentz frame in which it is at rest.
In this frame, the momentum is invariant under three-dimensional rotations.
Thus, the little group is O(3), leading to the concept of the spin. If
the particle moves, the little group is a Lorentz-boosted O(3) still with
three generators.
- You may wonder whether all these can be found in a single book. Yes, you can go to the Amazon.Com to order the book. This book covers also applications of the Lorentz group to current issues on optics and entanglements. If you do not want to purchase the book, you can borrow a copy from me. Send your request to yskim@umd.edu.
copyright@2016 by Y. S. Kim, unless otherwise specified.
Click here
for his home page.