I believe in
Feynman's One Physics.
|
- According to Feynman, we have to use Feynman diagrams for scattering
problems. As for Bound states, Feynman suggested harmonic oscillators
instead of Feynman diagrams. However,
the paper Feynman wrote with Kislinger and Ravndal is mathematically
inconsistent. However, by importing
Dirac's mathematics, it is possible to construct a covariant harmonic
oscillator formalism with the following properties.
- The formalism is fully consistent with all known principle of quantum mechanics and special relativity.
- Its wave functions carry a Lorentz-covariant probability wave interpretation.
- When applied to hadrons consisting of quarks, the same formalism produces the quark model for slow hadrons and Feynman's parton model for fast-moving hadrons.
Yes, indeed, we have a satisfactory bound-state model. On the other hand, it appears to be so different from Feynman diagrams that we are led to the question of whether these two different formalisms lead to the same physics. Feynman would ask this question if we do not.
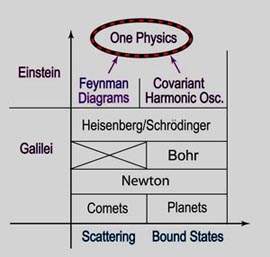
- A preliminary work has been done on this problem, and we can present
the history diagrams shown on this webpage. The key to this question is
both Feynman diagrams and the covariant oscillator formalism allow
off-mass shell energy-monemtum relations.
We all know how particles become off-shell in Feynman diagrams. Observable hadrons are on their mass shells, but quarks inside the hadron are not their mass shells. This is the key to the answer, and both Feynman diagrams and covariant oscillators lead to the same physics. This is the way Feynman wanted or still wants to do physics. For a published paper on this subject, Click here.
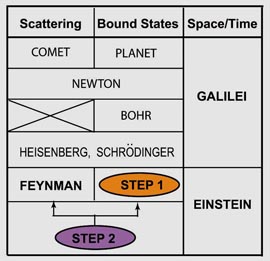
Let us look at the history of physics. The difference between comets and planets has been a constant head ache to human beings. It was not until Newton to see that they are the same thing. In quantum world, Bohr intoduced a model for quantized bound states, but was not able to explain scattering problems. Schroedinger and Heisenberg solved this problem and unified both scattering and bound-state problems. As we all know, it was a great leap forward in physics.
Can then Schroedinger's picture be extended to Einstein's relativistic world? If we approched this problem through two separate routes, one for scattering states and the other for bound states, we have no apologies. The only problem is to show that they lead to the one and same physics.
The difference between an ellipse and hyperbola has also been a big head ache to scientists, especially to mathematicians. They introduced a cone to unify these two geometrical objects. They can be combined into one word "conic section."
We have seen how physicists do conic sections by inventing dynamics which can explain both scattering and bound-state problems. You do not have to be this ambitious. There are many small problems in physics having to do with placing circles and hyperbolas into one package. You will be surprised to see that the ultilayer problem in ray optics can accommodate this interesting problem. You may click here for a published paper on this problem.
Further Contents of Lorentz Invariance

|
However, my feeling was that we should be able to add some other figures to those hyperbolas. With this point in mind, I read Dirac's papers.
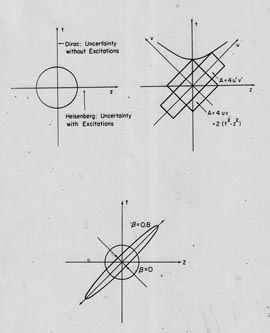
|
This is one way to combine quantum mechanics with special relativity, and is also one way to combine hyperbola with ellipse.
To many people, this ellipse is known as the squeezed state of light.
Y.S.Kim (2007.9.15)