Dirac's Lorentz Covariance

|
-
The word "Lorentz Violation" is mentioned quite often these days. Does
this mean Einstein was wrong in 1905? It is possible but is highly unlikely.
Then what does this word mean?
We write many formulas in physics, but we often are not able to see its contents in Einstein's Lorentz-covariant world. If their formulas can explain everything other than Lorentz covariance, it could be a Lorentz violation.
Then, the present form of non-relativistic quantum mechanics constitutes a Lorentz violation. This was one of Dirac's life-long concerns. I often brag about my audience with him in 1962. I had my second audience in 1978. By 1978, I had studied many of Dirac's papers and was able to ask him key questions.
Dirac did not think the Copenhagen view of quantum mechanics is completely satisfactory, but we should live with wave functions and and their probabilistic interpretation. He added that we should worry about the Lorentz covariance of wave functions. What he said was quite consistent with the papers he had published by that time.
Let us look at some of his papers.
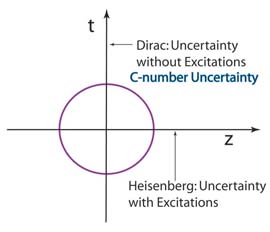
1927. Dirac's First Lorentz Violation
-
In his paper published in Proc. Roy. Soc. (London) A114,
243 (1927), Dirac observes that there is an uncertainty relation
between the time and energy variables which enables radiation
decays. He observes that there are no excitations along the
time axis. This space-time asymmetry makes it very difficult
to combine quantum mechanics with special relativity.
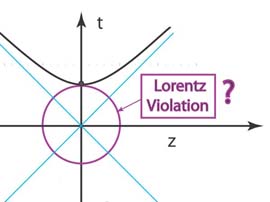
1945. Dirac's Second Lorentz Violation
|
-
In his paper in Proc. Roy. Soc. (London) A183 (1945), Dirac's
observes that quantum mechanics is a physics of harmonic oscillators
and that special relativity is a physics of the Lorentz group. Thus
it may be possible to combine quantum mechanics with relativity by
constructing a representation of the Lorentz group using harmonic
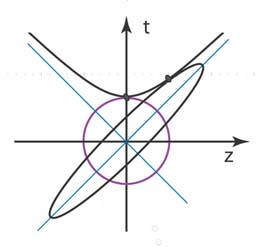
oscillators. He wants to have localized wave functions also in
the time variable. As a consequence, he ends up with the Gaussian form
exp{-(z2 + t2)} ,
which is localized within the circular region shown with the Lorentz-invariant hyperbola. The circle given does not appear to be consistent with special relativity. This constitutes Dirac's second Lorentz violation.
|
1963. Dirac's Coupled Oscillators
-
In his paper,
J. Math. Phys. 4 , 901 (1963), Dirac considers two
coupled harmonic oscillators, and ended up with a representation of the
O(3,2) deSitter group which contains the O(3,1) Lorentz group as a subgroup.
Some years later, it was found that the
oscillator coupling corresponds to the Lorentz boost.
1949. Dirac's Third Lorentz Violation
|
|
-
In his classic paper in
Rev. Mod. Phys. 21 , 392 (1949),
Dirac considers three possible forms of relativistic quantum mechanics.
However, in all of the three cases, he ends up with the "real problem" of
particles on their mass shells. At that time, Feynman diagrams did not
exist, the concept of off-mass shell particle did not exist.
These days, it is a widely accepted view that particles in bound states are not necessarily on their mass shells. Click here for further details.
In the same paper, Dirac introduces the light-cone coordinate system.
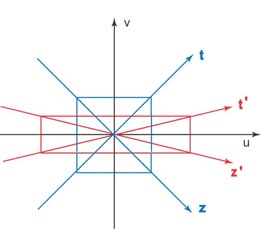
These Lorentz Violations disappear if we combine all three
Violations.
|
-
It is not difficult to produce this figure by combining all three
of the above figures. In so doing, we can construct a representation
Poincaré group for relativistic extended particles.
This result is not surprising in view of
Dirac's 1963 paper on coupled oscillators, but it took some years to
appreciate this point.
Paul A. M. Dirac is known as a great physicist who produced physics by creating beautiful algebras. It is gratifying to note that his algebraic language can be translated into beautiful geometries. During this process, we can achieve a better understanding of physics.
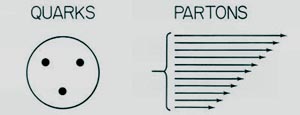
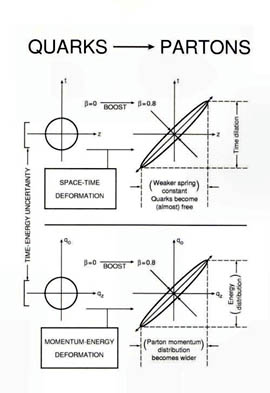
Feynman's Parton Picture
-
Indeed, it is possible to show that the quark model and parton model
are two limiting cases of one Lorentz-covariant theory constructed
as above.
|
| ||||
| ||||
| ||||
|
-
The parton model is valid in the limit of light speed. The
question is how about in between. We can talk about
the proton form factor.
Proton Form Factors
|
-
The proton is the first hadron we can think of. It is known to have
an extended charge distribution, observed in the electron-proton
scattering. The scattering amplitude without the electronic
component called the proton form factor.
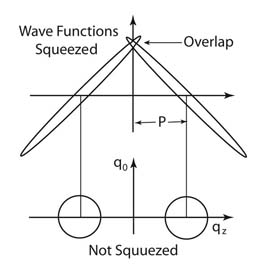
If the incoming electrons are not fast, and the recoil effect of the proton can be ignored, the form factor is the Fourier transformation of the charge distribution with respect to the momentum transfer.
The question is what happens when the electron energy becomes high, and the momentum transfer becomes large. According to what we observe in high-energy labs, the form factor shows a dipole decrease, even though there are some recent deviations discussed in the literature.
This dipole decrease can be interpreted in terms of the overlapping wave functions shown in this figure. We need a more extensive webpage explain fully what is going on here, and I intend to construct this webpage in the future. This figure is from my book with Marilyn Noz.