This experimental signal in this case study was unusual because it did not look like a typical signal when plotted; in fact, it looked a lot like noise at first glance. The figure below compares the raw signal (bottom) with the same number of points of normally-distributed white noise (top) with a mean of zero and a standard deviation of 1.0 (obtained from the Matlab/Octave 'randn' function).
As you
can see, the main difference is that the signal has more
large 'spikes', especially in the positive direction.
This difference is evident when you look at the descriptive
statistics of the signal and the randn function:
|
DESCRIPTIVE STATISTICS |
Raw signal |
random noise |
|
Mean |
0.4 |
0 |
|
Maximum |
38 |
about 5 - 6 |
|
Standard Deviation (STD) |
1.05 |
1.0 |
|
Inter-Quartile Range (IQR) |
1.04 |
1.3489 |
|
Kurtosis |
38 |
3 |
|
Skewness |
1.64 |
0 |
You can see that the standard
deviations of these two are nearly the same, but the other
statistics (especially the kurtosis
and
skewness) indicate that the probability
distribution o f the signal is far from normal; there are far
more positive spikes in the signal than expected for pure
noise. Most of these turned out to be the peaks of interest
for this signal; they look like spikes only because the
length of the signal (over 1,000,000 points)
causes
the peaks to be compressed into one screen pixel or less
when the entire signal is plotted on the screen. In the
figures on the left, iSignal is used to "zoom in"
on some of the larger of these peaks (using the cursor arrow
keys). The peaks are very sparsely separated (by an average
of 1000 half-widths between peaks) and are well above the
level of background noise (which has a standard deviation of
roughly 0.9 throughout the signal).
f the signal is far from normal; there are far
more positive spikes in the signal than expected for pure
noise. Most of these turned out to be the peaks of interest
for this signal; they look like spikes only because the
length of the signal (over 1,000,000 points)
causes
the peaks to be compressed into one screen pixel or less
when the entire signal is plotted on the screen. In the
figures on the left, iSignal is used to "zoom in"
on some of the larger of these peaks (using the cursor arrow
keys). The peaks are very sparsely separated (by an average
of 1000 half-widths between peaks) and are well above the
level of background noise (which has a standard deviation of
roughly 0.9 throughout the signal).
The researcher
who
obtained this signal said that a 'good' peak was 'bell
shaped', with an amplitude above 5 and a width of 500-1000
x-axis units. So that means that we can expect the
signal-to-background-noise ratio to be at least 5/0.9 =
5.5. You can see in the three example peaks on the left that
the peak widths do indeed meet those expectations. The
interval between adjacent x-axis points is 25, so that means
the we can expect the peaks to have about 20 to 40 points in
their widths. Based on t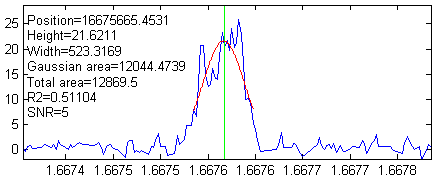 hat, we can expect
that the positions, heights and widths of the peaks should
be able to be be measured fairly accurately using
least-squares methods (which reduce the uncertainty of
measured parameters by about the square root of the number
of points used - about a factor of 5 in this case). However,
the noise appears to be signal-dependent; the noise on the
top of the peaks is distinctly greater than the noise on the
baseline. The result is that the actual signal-to-noise
(S/N) ratio of peak parameter measurement for the larger
peaks will not be as good as might be expected based on the
ratio of the peak height to the noise on the background.
Most likely, the total noise in this signal is the sum
of two major components, one with a fixed standard deviation
of 0.9 and the other roughly equal to 10% of the peak
height.
hat, we can expect
that the positions, heights and widths of the peaks should
be able to be be measured fairly accurately using
least-squares methods (which reduce the uncertainty of
measured parameters by about the square root of the number
of points used - about a factor of 5 in this case). However,
the noise appears to be signal-dependent; the noise on the
top of the peaks is distinctly greater than the noise on the
baseline. The result is that the actual signal-to-noise
(S/N) ratio of peak parameter measurement for the larger
peaks will not be as good as might be expected based on the
ratio of the peak height to the noise on the background.
Most likely, the total noise in this signal is the sum
of two major components, one with a fixed standard deviation
of 0.9 and the other roughly equal to 10% of the peak
height.

To automate the detection of large numbers of peaks, we can
use the findpeaksG or iPeak functions. Reasonable
values of the input arguments AmplitudeThreshold, SlopeThreshold, SmoothWidth, and FitWidth
for those
functions can be estimated based on the expected peak height
(5) and width (20 to 40 data points) of the "good" peaks. For
example, using  AmplitudeThreshold=5, SlopeThreshold=.001, SmoothWidth=25, and FitWidth=25, these function
detect and measure 76 peaks above an amplitude of 5 and with
an average peak width of 523. The interactive iPeak function is especially
convenient for exploring the effect of these peak detection
parameters and for graphically inspecting the peaks that it
finds. Ideally the objective is to find a set of peak
detection arguments that detect and accurately measure all
the peaks that you would consider 'good' and skip all the
'bad' ones. But in reality the criteria for good and bad
peaks is at least partly subjective, so it's usually best to
err on the side of caution and avoid skipping 'good' peaks
at the risk of including a few 'bad' peaks in the mix, which
can be weeded out manually based on unusual position,
height, width, or appearance.
AmplitudeThreshold=5, SlopeThreshold=.001, SmoothWidth=25, and FitWidth=25, these function
detect and measure 76 peaks above an amplitude of 5 and with
an average peak width of 523. The interactive iPeak function is especially
convenient for exploring the effect of these peak detection
parameters and for graphically inspecting the peaks that it
finds. Ideally the objective is to find a set of peak
detection arguments that detect and accurately measure all
the peaks that you would consider 'good' and skip all the
'bad' ones. But in reality the criteria for good and bad
peaks is at least partly subjective, so it's usually best to
err on the side of caution and avoid skipping 'good' peaks
at the risk of including a few 'bad' peaks in the mix, which
can be weeded out manually based on unusual position,
height, width, or appearance.
Of
course, it must be expected that the values of the peak
position, height, and width given by the findpeaksG or iPeak functions will only be
approximate and will vary depending on the exact setting of
the peak detection arguments; the noisier the data, the
greater the uncertainty in the peak parameters. In this
regard the peak-fitting functions peakfit.m and ipf.m usually give more
accurate results, because they make use of all the data across the peak,
not just the top of the peak as do findpeaksG and
iPeak. For example, compare the results of the peak near
x=3035200 measured with iPeak (click to view) and with peakfit
(click to
view). Also, the peak fitting functions are better for
dealing with overlapping peaks and for estimating
the uncertainty of the measured peak parameters, using
the bootstrap options of those
functions. For example, the largest peak in this signal has
an x-axis position of 2.8683e+007, height of 32, and width
of 500; the bootstrap method determines that the
standard deviations are 4, 0.92, and 9.3,
respectively.
Because the signal in the case study was so large (over
1,000,000 points), the interactive programs such as iPeak, iSignal, and ipf
may be sluggish in operation, especially if your computer is
not fast computationally or graphically. If this is a
serious problem, it may be best to break the signal up into
two or more segments and deal with each segment separately,
then combine the results. Alternatively, you can use the condense function
to average the entire signal into a smaller number of points
by a factor of 2 or 3 (at the risk of slightly reducing peak
heights and increasing peak widths), but then you should
reduce SmoothWidth and FitWidth by the same factor
to compensate for the reduced number of data points across
the peaks. Run testcondense.m for a
demonstration of the condense function.