Unit III - Part B
3.3 Exponential Models
Among the most significant non-linear patterns of variation are those that
are modeled well by exponential relations. It's not at all uncommon
to read scientific or economic news reports that describe some variable
growing or decaying exponentially over time. Thus an understanding of exponential
change is useful in making sense of important practical events.
To understand the patterns of change that can be expected with exponentially
related variables, there are several basic questions that you should be
adept at dealing with:
* Given a situation where the relation between variables is described
by a set of data points, a graph, or some conditions described in words,
you should be able to recognize when the pattern seems likely to be well
modeled by an exponential rule and to express that rule in symbolic form.
* Given the rule for an exponential model, you should be able to interpret
that rule to describe the situation being modeled and to use the rule to
answer important questions about the situation.
The following problems have been selected to illustrate some of the many
important applications of exponential models and to develop your skill in
working with them.
If It Sounds Too Good To Be True . . . It Probably Is!
Human gullibility in the face of get-rich-quick schemes is legendary. It
is a failing that afflicts even the best and brightest and most ambitious
among us. For example, during the summer of 1994, newspaper and television
reports described eager Washington investors lining up to participate in
a chain-letter-type scheme called Airplane. The game starts when
a "pilot" recruits two "co-pilots" who join him in recruiting
four "crew members" who join in recruiting eight "passengers."
Each "passenger" pays an entry fee to the "pilot".
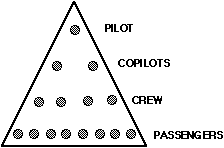
When the "airplane" is full, the pilot leaves the game and each
co-pilot takes half the crew members and half the passengers to start his
or her own "airplane."
If each passenger pays an entry fee of $1000, the "pilot" makes
$8,000. But there are some risks for potential players in such pyramid schemes.
What's the catch in pyramid schemes that makes them illegal in 46 states?
1. Work out answers to the following specific questions to help in reasoning
about
the "catch" and explaining it to someone else.
(a) Sketch diagrams of the airplanes formed at the next several stages of
the process.
(b) Make a table showing the numbers of passengers required to fill the
airplanes at each succeeding stage of the process:
Stage of Process 1 2 3 4 5 6 7 8 9 10 20 30
Passengers Required 8
2. The "pilot" who starts the game gets payments from each of
the copilots and crew members as well as the 8 passengers. Pilots who form
their own airplanes by splitting off from the original or some descendant
get money only from the passengers on their planes.
(a) How much money will the original pilot clear if all goes well?
(b) How much money will each succeeding pilot clear if all goes well?
(c) What is the total of money that will be paid by the passengers only
at stages 1, 2, 3, 4, ... , 10 of the game?
Some organizations need to spread accurate information to many people quickly.
One way to do this efficiently is by a telephone calling tree. For example,
the Madison Soccer Club has boys and girls from about 750 families who play
soccer each Saturday in the fall. When it is rainy, everyone wants to know
if the games are canceled. The club president makes a decision and then
starts calling. He calls two families, each of them calls two more families,
each of them calls two more families, and so on. This calling pattern can
be diagrammed by a tree that starts like this:
...
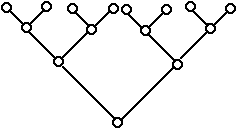
3. At the start of the calling process, only one club member, the president,
knows whether the game is on or not. In the first stage of calling, two
new people get the word. In the next stage, four others hear the decision,
and so on.
(a) Make a table showing the number of club members who will hear the decision
at each of the next 8 stages of the calling process. Then plot the data.
Stage of Calling 0 1 2 3 4 5 6 7 8 9 10
Tree
Members Who Hear 1 2 4 ...
(b) How does the number of members hearing the message grow as the calling
tree progresses in stages? How is that pattern of change shown in the plot
of the data?
(c) How many stages of the tree will be needed before all 750 families know
the decision? How many telephone calls will be required?
4. How will word pass through the club if each person in the tree calls
three other members, instead of just two?
(a) Sketch a tree diagram for several stages of this calling plan.
(b) Make a table showing the number of club members who will hear the decision
at each of the first ten stages of the calling process. Then plot the data.
Stage of Calling 0 1 2 3 4 5 6 7 8 9 10
Tree
Members Who Hear 1 3 ...
(c) How does the number of members hearing the message increase as the calling
tree progresses in stages? How is that pattern of change shown in the plot
of the data?
(d) How many stages of the tree will be needed before all 750 families know
the decision? How many telephone calls will be required?
5. Next suppose that the club president needs to consult with the other
four members of the club executive committee by a conference call before
making a decision about canceling a day's games. How will word pass through
the club if each person on the executive committee then calls two other
club families, they each call two other families and so on?
(a) Sketch a tree diagram for several stages of this calling plan.
(b) Make a table showing the number of club members who will hear the decision
at each of the first ten stages of the calling process. Then plot the data.
Stage of Calling 0 1 2 3 4 5 6 7 8 9 10
Tree
Members Who Hear 5 ...
(c) How does the number of members hearing the message increase as the calling
tree progresses in stages? How is that pattern of change shown in the plot
of the data?
(d) How many stages of the tree will be needed before all 750 families know
the decision? How many telephone calls will be required?
6. The procedures for calculating numbers of people informed at each stage
of a calling tree can be described in several different ways with algebraic
equations and then computed with help of a graphing calculator.
(a) You've undoubtedly noticed that the number of families learning the
play/no-play decision at each stage depends on the number who heard at the
previous stage. Use the words NOW and NEXT to write an equation showing
this pattern of information spread in (3). Then adjust the equation to find
rules for (4) and for (5).
(b) Try this key sequence on your graphing calculator, notice the results,
and figure out what the calculator is doing:
Press 1 and then ;
Press then 2 and then again;
Press repeatedly.
Then vary the procedure so it will produce the results of problem (4).
Then vary the procedure so it will produce the results of problem (5).
(d) Most calculators also have a key that is also helpful in these situations.
Explore the output of the rule y = 2^x using the calculator's table command
to make a table of (x,y) values for x = 0 to x = 20 or higher.
(d) What modification of the rule in (c) will give the calculations required
in problem (4)? How about problem (5)?
(e) What calculations are invoked by the instruction 2^x and how is that
direction written in standard algebraic notation for each of the calling
tree variations?
The patterns of information spread in a calling tree occur in many other
quite different situations. For example, if bacteria infect some part of
your body, the infection spreads when the bacteria grow and split into two
genetically equivalent cells that grow and split again and again.
7. Suppose a single bacterium lands in a cut on your hand and begins spreading
an infection by growing and splitting into two bacteria every 20 minutes.
(a) Make a table showing the number of bacteria after each twenty minute
period in three hours (assuming none of the bacteria are killed by white
blood cells). Plot the (time periods, bacteria count) data.
Describe the pattern of growth of bacteria causing the infection.
(b) Use NOW and NEXT to write an equation relating the number of bacteria
at one time to the number 20 minutes later. Then use the equation and your
calculator to find the number of bacteria after 15 twenty-minute periods.
(c) Write an equation in the form "y = " showing how the number
of bacteria after any number of 20-minute periods can be calculated without
finding the number at all intermediate times. Use that equation, the list,
and the command of your calculator to check the results of (a) and (b).
(d) How would the rules for predicting bacteria growth change if the process
began with 20 or 500 bacteria instead of a single one:
(i) What would the NOW ... NEXT equations become?
(ii) What would the "y = " equations become?
(e) How are the table, graph, and equations of bacteria growth similar to
and different from the calling tree examples and typical patterns of linear
models?
(f) One of the most common illnesses in young people is strep throat--a
bacterial infection that can cause painful sore throats. How does what you
have learned about exponential growth explain the way such strep throats
seem to develop very quickly?
8. Jurassic Park , the popular book and movie about a dinosaur theme
park, is loosely based on the idea that ancient dinosaur DNA might be recovered
from fossils and copied in laboratories until the genetic material for dinosaurs
was available. The possibility of actually "recreating" dinosaurs
is remote. But chemists have invented processes for copying genetic materials.
The 1993 Nobel Prize for chemistry was shared by two scientists who developed
such processes. In the PCR (polymerase chain reaction) process invented
by Kary Mullis, a sample of DNA is doubled by an operation that takes about
5 minutes.
(a) Suppose a chemist starts the PCR process with a sample that holds only
7 copies of a special piece of DNA.
(i) Write two different equations that can be used for calculating the number
of copies of that DNA that will be on hand in a series of 5-minute periods.
(ii) Use either of your equations from above to find the number of copies
of the DNA produced after 2 hours.
(iii) Use your equations to find the number of 5-minute periods required
to first produce 1 billion copies of the DNA.
(b) How would your answers to part (a) change if the starting DNA sample
held 10, 20, or 30 copies of the DNA to be copied?
9. The sketch below shows the first stages in formation of a geometric design
called a fractal . At each stage in growth of the design, the middle
of every segment is replaced by a triangular tent. The new design is made
up of more, but shorter, segments. The name fractal is used for designs
in which small parts have shape that is similar to that of the whole figure.

(a) Make a sketch showing at least one more stage in the growth of this
fractal design.
(b) Continue the pattern begun in this table:
Stage of Growth 0 1 2 3 4 5 6 7
Segments in Design 1 4 ...
(c) Write an equation using NOW and NEXT to show how the number of segments
at any stage of the design can be used to find the number at the next stage.
(d) Write a rule that can be used to find the number of segments in the
pattern at any stage x , without finding the numbers at each stage
along the way.
(e) Use the rule and your calculator to produce a table and a graph showing
the number of segments in the fractal pattern at each of the first 10 stages
of growth and at the 20th and 30th stages.
(f) At what stage will the number of small segments first reach 1 million?
*(g) In moving from one stage to the next in the fractal design, each segment
is divided into three equal length parts and a tent is raised over the middle
section with sides equal in length to the parts on each side.
(i). If the original line segment is one inch long, how long is each segment
of the pattern in stage 2? In stage 3? In stage x?
(ii) How long is the total fractal pattern at any stage x? [Hint: Combine
the number of segments at stage x with the length of each segment at that
stage.]
Conclusions and Connections
1. When you compare the situations, tables, graphs, and equations
modeling the patterns in questions 1-9, what similarities do you see in
all cases? What differences?
2. When you compare the equations y = 3 + 2x and y = 3(2), what do the numbers
3 and 2 tell in each case about patterns in tables and graphs?
3. What information can you tell in general about the patterns in tables
and graphs
of exponential models with rules of the form y = A(b)?
The examples of related changing variables in questions 1-9 all involved
some quantity increasing as time passed. Of course, in many cases important
quantities decrease as time passes or as some other variable increases.
One very simple and familiar example is the pattern of heights for a bouncing
ball.
10. Most popular American sports involve balls of some sort. In playing
with those balls one of the most important factors is the bounciness or
elasticity of the ball. For example, if a new golf ball is dropped onto
a hard surface, it should rebound to about of its drop height. Suppose a
high shot drops downward from a height of 27 feet onto a road and keeps
bouncing up and down again and again.
(a) Make a table and plot of the data showing expected heights of the first
ten bounces.
Bounce Number 0 1 2 3 4 5 6 7 ...
Rebound 27 ...
Height
(b) How does the rebound height change from one bounce to the next? How
is that pattern shown by the shape of the data plot?
(c) What equation relating NOW and NEXT shows how to calculate the rebound
height for any bounce from the height of the preceding bounce?
(d) What equation helps estimate the rebound height after any number of
bounces?
(e) How will the data table, plot, and equations for calculating rebound
height change if the ball drops first from only 15 feet?
As is the case with all mathematical models, data from actual tests of golf
ball bouncing will not match exactly the predictions from equations of ideal
bounces. You can simulate the kind of quality control testing that factories
do by running some experiments in your classroom:
11. Get a golf ball and a tape measure or meter stick and collect data on
the rebound height for successive bounces of the ball. Compare the pattern
of your data to that predicted by the model based on the goal of rebound
to of drop height. See if a factor other than might give a better model.
12. To see if the bouncing ball data pattern applies to other balls, repeat
the experiment with a tennis ball or a basketball. In those cases you will
have to study the data to find a reasonable estimate of the rebound height
factor. Instead of testing a specific model, you will be using data to help
discover a mathematical model of the bouncing behavior.
One of the amazing properties of mathematical ideas is that patterns discovered
in one context turn up in quite different and unexpected places. Then calculations
done the first time can be applied to the new situations. This recurrence
of fundamental patterns is an especially impressive property of exponential
models.
For example, drugs are a very important part of the human health equation.
Many drugs are essential in preventing and curing serious physical and mental
illnesses; many other drugs cause damaging addiction and physical or mental
impairment.

For the 5 million Americans of all ages who suffer from diabetes, insulin
is an extremely valuable drug. To provide that essential hormone, when the
body's pancreas production fails, diabetics take the drug insulin. However,
once in the blood stream, insulin begins breaking down into other chemicals
and soon passes from the body. A typical pattern of decrease for insulin
in the blood is shown in the following graph.
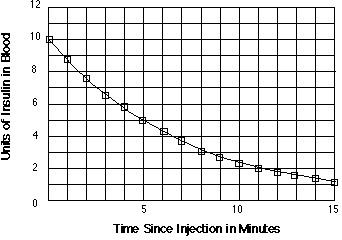
13. Medical scientists are usually interested in the time is takes for a
drug to be reduced to one half of the original dose. They call this time
the half-life of the drug. What appears to be the half-life of insulin?
14. The pattern of decay shown on the graph for insulin can be modeled well
by an exponential equation in the form y = A(b) .
(a) Enter five or six data points from the given graph and use the calculator
menu to find the values of A and b that give its recommended best fitting
model [Choose ExpReg, which you can scroll down to find on the and menus.]
(b) Test the calculator-generated rule to see how well data and graphs it
produces fit the pattern in the given information.
(c) Explain what the values of A and b tell about the action of insulin
in the blood.
(d) What equation relating NOW and NEXT would show how the amount of insulin
in the blood changes from one minute to the next if only one shot is given
directly into the blood stream?
[Because insulin decays and is filtered out of the blood so quickly, there
are various medical procedures used to provide a sort of timed-release supply,
rather than a single quick shot directly into the blood stream.]
15. The insulin graph shows data points for each minute following the original
dose. But the curve connecting those points reminds us that the insulin
breakdown does not occur in sudden bursts at the end of each minute! It
occurs continuously as time passes.
One quite reasonable model for that pattern is y = 10(0.9). What would each
of the following calculations tell about the insulin decay situation, and,
based on the graph above, what would you expect as reasonable values for
those calculations?
(a) 10(0.9 ) (b) 10(0.9)
(c) 10(0.9 )
16. Mathematicians have figured out ways to do calculations with fractional
exponents so that the results fit in the pattern from whole number exponents.
One of those methods is built into your graphing calculator. Enter the rule
y = 10(0.9^x) in the menu of your calculator and then complete the
following table of values showing the insulin decay pattern at times other
than whole hour intervals.
Time in minutes 0 0.5 1.5 2.5 3.5 4.5 5.5 6.5
Insulin in blood 10
Then compare the entries in this table with data shown by points on the
earlier graph.
17. The most famous antibiotic drug is penicillin. After its discovery in
1929, it became known as the first miracle drug, because it is so
effective in fighting serious bacterial infections. Drugs act somewhat differently
on each person, but, on average, a dose of penicillin will be broken down
in the blood so that one hour after injection only 60% will remain active.
Suppose a hospital patient is given an injection of 300 milligrams of penicillin
at noon.
(a) Write an equation of the form y = a (b ) that can be used to calculate
the amount of penicillin remaining after any number of hours x .
(b) Make a table showing the amount of that penicillin that will remain
at half-hour intervals from noon until 5 pm.
(c) Sketch a graph of the relation from part (a) and explain what the pattern
of that graph shows about the rate at which penicillin decays in the blood.
(d) Use the equation from (a) and tables and/or graphs it produces to find
the time when less than 10 mg remain.
(e) Find the half-life of penicillin in a typical patient--the time when
half the original dose has broken down in the blood. Will this half-life
be different for different initial dose sizes? [Try some variations on the
300 mg dose.]
Most harmful addictive drugs are illegal to possess and to use. In many
situations drug tests are used to detect and screen out users. Most drugs
decay in the human blood stream in patterns that are modeled well by exponential
rules.
18. Some athletes try using anabolic steroid drugs to increase their weight
and strength. Unfortunately, those drugs have very damaging side-effects
and the drugs leave the human body fairly slowly. With an injection of the
steroid ciprionate, about 90% of the drug and its by-products will
remain in the body one day later. Then 90% of that amount will remain after
a second day, and so on.
Suppose that an athlete tries steroids and injects a dose of 100 milligrams
of ciprionate. Analyze the pattern of that drug in the athlete's body by
answering the following questions.
(a) Make a table showing amount of the drug remaining in the user's blood
stream at various times.
Time since use (days) 0 1 2 3 4 5 6 7
Steroid present (mg) 100 90 81 ...
(b) Make a plot of the data in part (a) and write a short description of
the pattern shown in the table and the plot.
(c) Write two equations that describe the pattern of steroid in the drug
user's blood.
* Write one equation showing how the amount of drug changes from one day
to the next.
* Write a second equation in the form y = A (b) that shows how one could
calculate the amount of drug after any number of days.
(d) Use your calculator and one of the rules in part (c) to estimate the
amount of steroid left in the drug user's blood after 0.5 and 8.5 days.
(e) Find the half-life of this steroid and see if that time depends on the
size of the original dose.
(f) Drug tests, like those used in the Olympic Games are very sensitive.
How long will it take the steroid to be reduced to only 1% of its original
level in the blood? That is, how many days will it take for 99 milligrams
to be removed from the original dose?
19. Cocaine is a dangerous drug that some people use for "recreation."
It metabolizes in the blood rapidly. One hour after ingestion, half the
original amount of cocaine has decayed into other chemicals and that halving
process continues the next hour and so on.
Suppose a drug addict gets 50 milligrams of cocaine into the blood stream.
(a). How much of that 50 mg will remain in the addict's system after:
* 1 hour?
* 2 hours?
* 3 hours?
(b) Write an equation for calculating the amount of cocaine that will remain
x hours after the initial dose.
(c) Use the equation from part (b) and your calculator to make a table showing
the amount of cocaine left at half-hour intervals from 0 to 5 hours. Then
sketch a graph showing the pattern of decay for that drug over the five
hour time interval.
(d) Tests for drugs are very sensitive; they detect even small amounts in
the blood. How long will it take the 50 milligram does of cocaine to decay
to less than 0.05 milligrams?
20. A key ingredient in the illegal drug marijuana is the chemical Delta-9-THC.
If 10 milligrams of Delta-9-THC are introduced to the blood stream of a
typical adult, 70% of that chemical will still be present one day later.
After another day, 70% of that amount will remain, and so on.
(a) Write two different equations that can be used to calculate the amount
of a 10 milligram dose of Delta-9-THC remaining in the body after any number
of days.
(b) What is the half-life of Delta-9-THC?
(c) How long will it take for the original 10 milligram dose to be reduced
to 0.1 milligrams? Show how the answer to this question can be found in
a table of (time, drug amount) data and in a graph of that
data.
21. Radioactive materials have many important uses in the modern world--from
fuel for power plants to medical x-rays and cancer treatments. But the radioactivity
that produces energy and tools for "seeing" inside our bodies
has some dangerous effects too. The wastes from production and testing of
nuclear weapons continue emitting damaging radiation for years.
The radioactive chemical strontium-90 is produced in many nuclear reactions
and, if absorbed in the food chain, can cause cancer in humans. It decays
rather slowly--if any amount is stored at the beginning of a year, 98% of
that amount will still be present at the end of that year.
(a) If 100 grams of strontium-90 are released in an accident at a nuclear
power plant, how much of that radioactive substance will still be around
after 1 year? After 2 years? After 3 years?
(b) Write two different equations that can be used to calculate the amount
of strontium-90 remaining at any year in the future, from an initial 100
grams.
(c) Make a table and a grpah showing the amount of strontium-90 that will
remain from an initial amount of 100 grams at the end of every 10 year period
during a century:
Years 0 10 20 30 40 50 ...
Amount left (g) 100 ...
(d) Use one of the equations in part (b) to find the amount of strontium-90
left from an initial amount of 100 grams after 15.5 years.
(e) Use one of the equations from part (b) to find the half-life of strontium-90.
(f) Use one of the equations from part (b) to find the number of years that
must pass until only 10 grams remain.
The next sketches show several stages in evolution of one of the most interesting
and famous fractal patterns, the Sierpinski Carpet, names after a Polish
mathematician. Starting with a solid square "carpet" one meter
on a side, smaller and smaller squares are cut out of the original in a
sequence of steps. Notice how, in typical fractal style, small pieces of
the design are similar to the design as a whole.
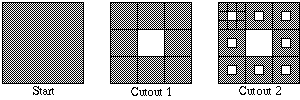
22. At the start of a Sierpinski carpet there is one square meter of carpet.
But as cutting proceeds, there seems to be less and less carpet and more
and more hole.
(a) Make a sketch showing the new holes that will appear in the third cutout
from the carpet.
(b) The carpet begins with an area of 1 square meter.
(i) How much of the original carpet remains after the first cutout?
(ii) What fraction of the carpet left by the first cutout remains even after
the second cutout. How much of the original 1 square meter of carpet remains
after the second cutout?
(iii) What fraction of the carpet left by the second cutout remains even
after the third cutout. How much of the original 1 square meter of carpet
remains after the third cutout?
(c) Following the pattern in the first three stages, how much of the original
1 square meter of carpet will remain after cutout 4? How about after cutout
5?
(d) What equation shows the relation between carpet area at any stage and
the next?
(e) What areas would you predict for the carpet left after cutouts 10? 20?
30?
(f) What equation would allow you to calculate the area of the remaining
carpet after any cutout x without going through all the cutouts from 1 to
x?
(g) What modeling equation would give area of the carpet after x cutout
stages if the original carpet had an area of 9 square meters, instead of
only 1?
Conclusions and Connections
1. Compare the equations, tables, and graphs for the bouncing ball, Sierpinski
carpets, drug decay, and radioactivity decay relations.
(a) In what ways are all examples similar?
(b) In what ways do they differ?
(c) How are the decay examples similar to and different from the exponential
growth examples?
2. For an equation of the form y = A(b), what conclusions can you draw about
the tables and the graphs of (x, y) values when:
(a) b is a number between 0 and 1?
(b) b is a number greater than 1?
3. For an equation of the form y = A (b) what conclusions can you draw about
the tables and the graphs of (x, y) values from the value of A?
4. Linear equations most often have the form y = mx + b.
(a) What do the values of m and b tell about the tables and graphs of
linear equations?
(b) How is the information provided by values of m and b in a linear
equation similar to and how different from that provided by A and b
in exponential equations like y = A (b)?
5. If you were asked to describe to someone the kinds of patterns of change
that are modeled well by exponential rules, what characteristics would you
mention and what examples would you choose to make the most interesting,
effective, or powerful illustrations?
Our planet Earth is home for millions of different species of animal and
plant life. But biologists estimate that between 50 and 100 species of life
become extinct every day. Much loss is due to human actions that
change the environment for animal and plant life. The extinction of life
forms can often be reversed by protection of species and their habitat.
For example, the Kenai Peninsula of Alaska is a natural home for wolves,
moose, bear, and caribou. But, when a gold rush of 1895-96 brought thousands
of prospectors to the area, hunting and changes to the environment reduced
all those populations. Wolves disappeared from the Kenai by about 1915.
In the late 1950's a few wolves reappeared in the Kenai, and wolves were
protected from hunting in 1961. The graph shows Kenai wolf populations growth
under protection.

Think About This Situation
(a) How would you describe the pattern of change shown in this plot?
(b) How would you expect that pattern to continue?
(c) What mechanisms do you expect are at work to cause the observed pattern
of change?
In 1989 the oil tanker Exxon Valdez ran aground in waters near the Kenai
peninsula. Over 10 million gallons of oil spread on the waters and shoreline
of the area, again endangering wildlife. That oil spill was eventually cleaned
up - some evaporated, some was picked up by specially equipped boats, and
some sank to the ocean floor as sludge.
Even in a fairly small and contained situation, clean up of pollution is
not a simple matter. For scientists planning environmental cleanups, it
is important to be able to predict the pattern of dispersion in such contaminating
spills.
Suppose that someone spilled 20 ounces of a water-soluble pollutant into
a 15 gallon tropical fish tank. To avoid the messy and tricky task of draining
and cleaning the tank, the owner decided that each day she would remove
3 gallons of polluted water and replace it with clean water. How long do
you think it would take to remove all of the pollutant?
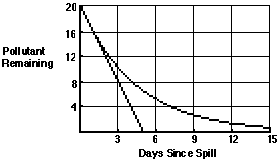
Think About This Situation
The two graphs on the diagram below show two possible patterns in removal
of the fish tank pollutant.
(a) What pattern of change is shown by each graph?
(b) Which shows the pattern of change that you would expect? Why?
The factors that cause populations to grow and chemical pollution to decline
in the ways that they usually do can be seen in some simple simulation experiments.
Try the following experiments, study the patterns of data they produce (using
data in table and scatter plot form), devise explanations for why those
patterns occurred, and then think of "real life" situations that
might behave in similar fashion.
Share the work on these experiments with different groups in the class and
then compare results. Have several groups do each experiment so you can
see similarities and differences in outcomes of the same and different experiments.
In each experiment, after you have read the directions ,make a prediction
of the pattern you expect to occur in the outcome data and record your thinking
that led to that prediction.
Experiment 1: Begin this experiment with a paper plate divided
into four sections, one of which is shaded, and a paper cup containing 200
kernels of unpopped popcorn.
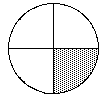
Pour the kernels of corn from the cup onto the plate at its center. Shake
the plate gently to spread the kernels around. Then remove all kernels that
end up on the shaded sector. Note the number of kernels removed and the
number remaining. Then repeat the pour-shake-remove process with the kernels
that remain.
(a) Collect the data from your experiment in a table like this:
Toss number 0 1 2 3 4 5 6 7
Kernels removed
Kernels left 200 ...
(b) Make a scatter plot of the (toss number, kernels left)
data.
(c) Describe and try to explain the pattern observed.
Experiment 2: Begin this experiment by pouring about 20 kernels of
corn onto a plate that as been divided into quarters, with one quarter shaded.
After shaking the plate to spread the kernels roughly evenly around, count
the number of kernels that land on the shaded sector of the plate. Add
that number of kernels to the test supply. Note the number of kernels
added and the new total supply. Repeat the pour-shake-count-add process
about 10 times.
(a) Record the data in a table of data like this:
Toss number 0 1 2 3 4 5 6 7
Kernels added 0
Kernels in supply 20 ...
(b) Plot the ((toss number, kernels in supply ) data.
(c) Describe and try to explain the pattern observed.
Experiment 3: Begin this experiment with a collection of about 200
identical coins. Toss those coins onto a flat surface and remove all coins
that land with heads up.
Toss the remaining coins again and remove all that land with heads up. Repeat
the toss and remove process to a total of about 8 trials.
(a) Record the data in a table of data like this:
Toss number 0 1 2 3 4 5 6 7
Coins removed 0
Coins in supply 200 ...
(b) Plot the ((toss number, coins in supply ) data.
(c) Describe and try to explain the pattern observed.
Experiment 4: Begin this experiment by tossing about 10 coins onto
a flat surface. Count the number of coins that land with heads down and
add that number of coins to the test supply. Note the number of coins added
and the new total of coins in your test supply. Repeat the toss-count-add
process to a total of at least ten trials.
(a) Record the data in a table of data like this:
Toss number 0 1 2 3 4 5 6 7
Coins added 0
Coins in supply 10 ...
(b) Plot the ((toss number, coins in supply ) data.
(c) Describe and try to explain the pattern observed.
Experiment 5: Begin this experiment with a supply of about 30 red and
120 white beads that have been thoroughly mixed in a bag or jar.
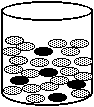
Remove a scoop of about 30 beads from the mixture (without looking at the
colors) and replace them with a scoop full of all white beads. Note the
number of red beads removed and the number remaining. Then shake the new
mixture. Repeat the remove/replace/mix process for a total of at least 10
trials.
(a) Record the data in a table of data like this:
Trial number 0 1 2 3 4 5 6 7
Red beads removed 0
Red beads in supply 30 ...
(b) Plot the ((trial number, red beads in supply ) data.
(c) Describe and try to explain the pattern observed.
3.4 Doing Business
Exponential models turn out to be useful in analyzing many kinds of business
situations. For example, it seems like every couple of weeks we hear about
somebody winning a big payoff in a state lottery somewhere. The wins can
be 1, 2, 5, or even as big as 50 million dollars. Those big money wins are
usually paid off in annual installments for about 20 years. How would you
react if this news report was actually about you?
College Park Student Wins Big Lottery
Prize--$50,000
A College Park One option is to
student has just won receive $5,000
$50,000 from a payments each year
Maryland lottery for the next 10
ticket that was a years. In the other
birthday present from plan the lottery will
friends. In a new invest $25,000 in a
lottery payoff special savings
scheme, the student account that will
(whose name has been earn 10% compound
withheld) has two interest for 10
payoff choices: years. At the end of
that time the student
will be paid the
balance in the
account.
Think About This Situation
Which of the two lottery payoff schemes would you choose, if it was you
who had just won the big prize?
(a) Which scheme do you think would give the greatest total payoff?
(b) How much money do you think you'll get after 10 years in the special
savings
account scheme?
The answers to these questions have a surprising connection to work you've
done in studying exponential growth patterns.
Of the two lottery payoff schemes, one has quite a simple rule: $5,000 per
year for 10 years, giving a total payoff of $50,000. The plan to put $25,000
in a savings account paying 10% compound interest might not be as familiar.
* After one year your balance will be
25,000 + (.10 x 25,000) = 1.10 x 25,000
= 27,500.
* After the second year your balance will be
27,500 + (.10 x 27,500) = 1.10 x 27,500
= 30,250
During the next year the savings account balance will increase in the same
way, starting from $30,250, and so on.
1. Write equations that will allow you to calculate the balance of this
deposit:
(a) For any year, from the year before.
(b) After any number of years x.
2. Use the equations from (1) to make a table and a graph showing the growth
of this special lottery savings account for a period of 10 years.
Time 0 1 2 3 4 5 6 7 8 9 10
$ 25,000 27,500 30,250 ...
3. Describe the pattern of growth in this savings account change as time
passes.
(a) Why is the balance not increasing at a constant rate (in dollars per
year)?
(b) How could the pattern of increase be predicted from the modeling rules?
(c) How long would it take to double the $25,000 savings account?
4. Compare the results in (2) to two other possible savings plans over 10
years:
(a) $35,000 earning only 5% annual interest.
(b) $15,000 earning 15% interest
The world population and populations of individual countries grow in much
the same pattern as money earning interest in a bank. For example,
* Mexico is the most populous country in Latin America, with a current
population of about 92 million. It is growing at a rate of 2.2% per year.
* Nigeria is the most populous country in Africa, with a current population
of 98 million. It is growing at a rate of 3.1% per year.
5. Make a table showing the predicted populations of these two countries
over the next 10 years. Then make a graph of the data for each country.
(a) Describe the patterns of growth expected in each country.
(b) Explain how the different patterns of growth are shown in the scatter
plots.
(c) What equations could be used to predict the populations of these countries
for any number of years x in the future?
(d) Use the equations from (c) to find out when:
(i) Mexico's population might reach 150 million.
(ii) Nigeria's population might reach 200 million.
6. In 1994 the population of Iraq was 19.9 million and growing at a rate
of 3.7% per year, one of the fastest growth rates in the world.
(a) Make a table showing the projected population of Iraq in each of the
next six years, to 2000.
(b) Write two different kinds of equations that could be used to calculate
population estimates for Iraq at any time in the future.
(c) Use one of the equations in part (b) to estimate the population of Iraq
in 2020.
(d) What factors might make the estimate of part (c) an inaccurate forecast?
7. One way to think about rates of growth is to calculate the time it will
take for a quantity to double in value. For example, it is common to ask
how long it will take a bank investment or a country's population to double.
(a) The U. S. population is currently about 260 million and growing exponentially
at a rate of 0.7% per year. How long will it take for our population to
double?
(b) If you calculate 0.7% of 260 million you get 1.82 million. How long
would it take the U. S. population to double if it increased linearly
at the rate of
1.82 million per year?
(c) How long does it take a bank deposit of $5,000 to double if it earns
interest compounded yearly at the rate of 2%? How about 4%? How about 6%?
How about 8%? How about 10%.
8. Suppose that at the birth of any child the government put $5,000 in a
special college savings fund earning 5% interest per year.
(a) Make a table and graph showing the value of that account each year for
18 years.
(b) How would the value of the account after 18 years be different if the
initial deposit was $10,000?
(c) How would the value of the account after 18 years be different if the
interest rate was 10% and the initial deposit was $5,000?
9. Banks frequently pay interest more often than once each year. Suppose
your bank pays interest compounded quarterly. If the annual percentage rate
is 4%, then the bank pays 1% interest at the end of each 3 month period.
(a) Explore the pattern of growth of a $1000 deposit in such a bank over
5 years (20 quarters).
(b) Compare the quarterly compounding with annual compounding at 4%.
(c) Repeat the calculations and comparisons if the annual rate is 8%.
Conclusions and Connections
1. What is there about money earning interest in the bank and growth of
human populations that makes it reasonable for them to grow in similar exponential
patterns?
2. Even though money in the bank might earn the same rate of interest over
a period of years, the actual dollar change in such an account increases
from one year to the next. Why is that happening?
3. Look back at the experiments you performed with popcorn, coins, and beads.
How do your explorations of exponential models help to explain the data
patterns observed in those earlier experiments?
4. In mid-1994 the world population was estimated to be 5.607 billion and
the
percent growth rate to be 1.6 percent. What do these estimates imply for
the growth in world population given in terms of
(a) People per hour
(b) People per day
(c) People per week
(d) People per month
(e) People per year
5. What is the estimated doubling time of world population, based on current
growth rate estimates? What are the consequences of such growth? What
factors might change everything?
6. What are the uses and limitations you can imagine for exponential models
of population growth?