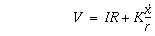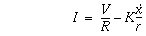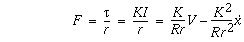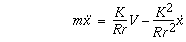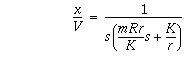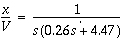Mathematical Model
The first step in any control system design is to model your system. The basic plant you'll be working with is a simple cart riding on a track. The track is assumed to be frictionless, and the cart is actuated by a voltage-controlled rotary motor which drives the cart's wheels through a gear system.
The differential equation of the frictionless cart of mass m is simply,
The system is driven by a DC motor with the following dynamics:
where I is the current through the motor, r is the radius of the gear connecting the motor to the track, K is a combined motor torque constant, and R is the resistive load of the motor. Solving this equation for I results in:
The torque produced by the motor is proportional to the current I,
Combining these relations, the applied force on the cart due to the motor is,
Substituting in the known system parameters m, R, r, and K results in the final transfer function,