Studio 4 : MATLAB for controls - state space analysis

State space modeling of dynamic LTI systems allows the control system designer to bring the vast array of tools from linear system theory to bear on the design problem. In addition to MatLab's standard selection of linear systems tools, a number of specialized state-space design and analysis tools are available through the Control Systems Toolbox.
Key Commands:

	ss		- conversion to state-space
	ssdata		- extraction of state-space data from a SYS model
	rss		- random stable state-space models
	ss2ss		- state transformations
	canon		- canonical state-space realizations
	ctrb		- controllability matrix
	obsv		- observability matrix

A. model creation using ss(), ssdata(), rss()

To begin, consider the same spring-mass-damper system from Lab 2:

The differential equation for this simple system is

.
An easy state-space form to convert this system into is the controllability canonical form (CCF). As you learned in lecture, this conversion is done using the following state definitions:

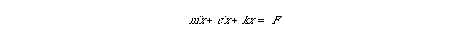	x1 = x
	x2 = dx/dt

In this manner, the CCF form of the system becomes:

The output equation in this state-space model assumes the system output is simply the mass position, x(t).

To create this state-space system within Matlab, use the ss() function, which generates a SYS object, just like the tf() command for transfer function system representations:

A = [0 1; -2/3 -8/3]
B = [0; 1/3]
C = [1 0]
D = 0
sys = ss(A, B, C, D)

Using this SYS object, all the MatLab system response tools such as step(), lsim(), etc., can be used on the state-space model of this system.

Given a SYS object, the component A, B, C, D matrices of the state-space model may be extracted using the ssdata() command, which has the following syntax:

        [A,B,C,D] = SSDATA(SYS) retrieves the matrix data A,B,C,D
        for the state-space model SYS.  If SYS is not a state-space 
        model, it is first converted to the state-space representation.

Finally, the rss() command may be used to generate a random state-space model. For full syntax, enter "help rss" within MatLab.

B. State transformations using ss2ss(), canon()

State transformations are important for converting between various canonical state-space forms, and for reconfiguring a given state-space models into a transformed model with controllable, uncontrollable, observable, and unobservable components decoupled.

Consider a state transformation z = Lx, where x is the original state vector, L is a linear transformation matrix, and z is the transformed state vector. Under this transformation, the resulting system becomes:

                .       -1        
                z = [LAL  ] z + [LB] u
                        -1
                y = [CL   ] z + D u

The ss2ss() function performs this transformation directly. For example, the system created in part A can be converted into diagonal canonical form using the following transformation discussed in lecture:

	x = Tz   where   T = [p1 p2 ... pn],  pi = ith eigenvector of A

First, note that MatLab's transformation is slightly different from lecture, where the transformation is defined as x = Tz (well, actually, we used "xbar" instead of "z" in class, but you get the idea). Thus, the MatLab transformation matrix L is the inverse of the transform T defined above.

Next, form the transform matrix T using the "eig()" function, which is defined as:

    	[V,D] = EIG(X) produces a diagonal matrix D of eigenvalues and a
    	full matrix V whose columns are the corresponding eigenvectors.

This, the desired transformation matrix is,

	[T,D] = eig(A)

Now the transformed system can be generated by entering:

	diagonalsys = ss2ss(sys, inv(T))

The resulting transformed A,B,C,D matrices can be extracted using ssdata():

       [Abar, Bbar, Cbar, Dbar] = ssdata(diagonalsys)

       Abar =
          -0.2792         0
           0.0000    -2.3874
       
       Bbar =
           0.1642
           0.4093
       
       Cbar =
           0.9632   -0.3863
       
       Dbar =
            0

Note that the A matrix has been converted to a diagonal form. Furthermore, the diagonal elements are -0.2792 and -2.3874, which corresponds to the eigenvalues of the original matrix A as was seen from the eig() command above. As discussed in lecture, this should be expected due to the invariance of the system's characteristic equation under any given similarity transformation.

Also, note that both eigenvalues of the system are negative. This implies that the unforced (natural, homogeneous) response of the system is stable, i.e. if you pull the mass to some initial position y(0) = x1(0) = yo, then both the displacement (x1) and velocity (x2) of the system will decay exponentially to y=0.

The above approach works for any given transformation, i.e. transformation into CCF or OCF. However, MatLab actually provides a more convenient method for converting a system into diagonal canonical form, using the "canon()" function. This is just a shortcut to what we did above, providing both the transformed system equations and the transformation matrix itself in a single function. Try entering:

	[diagonalsys2, L] = canon(sys, 'modal')   
		                                 (Q: why is it called "modal"?)

You should find that diagonalsys2 and the original diagonalsys are the same, and that the returned transformation matrix L is equal to the inverse of the eigenvector matrix T determined previously.

C. Controllability, observability matrices

Recall that the controllability matrix, U, and observability matrix, V, are defined as,

	U = [B  A*B  A^2*B ... A^(n-1)*B]
`
	V = [C C*A C*A^2 ... C*A^(n-1)]'	(note the transpose here)

The MatLab ctrb() and obsv() functions will create these matrices for you automatically. For example, the observability matrix for our 2-state spring-mass-damper example can be found by hand, and by ctrb(), as follows:

	U1 = [B A*B]

		U1 =
       		0    	0.3333
    		0.3333  0.2222

	U2 = ctrb(sys)

		U2 =
       		0    	0.3333
    		0.3333  0.2222

Clearly, the output is the same. This can save a bit of effort for many important operations, such as when forming transformation matrices for conversion to CCF or OCF which require U and V, respectively.

D. State-space / transfer function conversion

you can readily convert back-and-forth between state-space and transfer function representations of an LTI system using MatLab. Once you have a MatLab SYS object defined as in part A, the transfer function form of the system is found through "tf(sys)". Similarly, given a SYS object created from a transfer function, a state-space model of the system can be found using "ss(sys)". For example, convert the state-space model in part A as follows:

	sys2 = tf(sys)

		Transfer function:
		        0.3333
		----------------------
		s^2 + 2.667 s + 0.6667

Now convert it back to state-space form as,

	sys3 = ss(sys2);
	[A3 B3 C3 D3] = ssdata(sys2)

		A3 =
   			-2.6667   -0.6667
    			1.0000         0
	
		B3 =
    			0.5000
         		0
	
		C3 =
         		0    0.6667
	
		D3 =
     			0

Uh oh, the new state-space system isn't the same as the original system. What hapened? When MatLab does the TF -> SS conversion, it doesn't necessarily pick the same states that we used to generate the controllability canonical form we chose in part A. However, this simply means a similarity transformation is needed to convert between the two systems - the dynamics of the two systems are identical.

Assignment:

Note: you must turn in all m-files and m-fil output for these problems.

Consider the following differential equation:

 ...      .
3 x  +  2 x  -  x = 2 u

      ..
y = 5 x   +  5 u

1. CCF transformation

a. Convert the system into controllability canonical form (CCF) by hand.

b. Derive the transfer function G(s) of the system by hand.

c. Write an m-file to create G(s) in MatLab, then convert the system into a state-space representation.

d. Now, convert the system into CCF by creating the transformation x = P xbar, where P is the transformation matrix P = U*M, and U and M are defined as in lecture. Note that U can be readily generated within MatLab.

e. Should your result from 2d match your result from 2a? Why or why not?

3. OCF transformation

Adding to your m-file, transform the system to OCF.

4. Matlab diagonalization

a. Determine the eigenvalues and eigenvectors of the A matrix in your m-file.

b. From 4a, should the diagonalized A matrix have the eigenvalues on its diagonal? Why or why not?

c. First, using the "canon()" function, diagonalize the system.

d. Second, diagonalize the system within MatLab by forming the diagonalization transformation matrix as discussed in lecture.