ENME462
Studio 8
State Space Design
This studio is adapted from the CMU / U. Michigan control
system tutorial web site
Key Matlab commands: acker,
lsim, place, rscale
Assignment: there is no assignment for this studio. Please
pay attention during the studio and try to connect what you have learned in
class with this real-world design example.
State-space equations
There are several different ways to describe a system of linear differential
equations. The state-space representation is given by the equations:
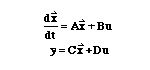
where x is an n by 1 vector representing the state (commonly position and velocity
variables in mechanical systems), u is a scalar representing the input (commonly
a force or torque in mechanical systems), and y is a scalar representing the
output. The matrices A (n by n), B (n by 1), and C (1 by n) determine the relationships
between the state and input and output variables. Note that there are n first-order
differential equations. State space representation can also be used for systems
with multiple inputs and outputs (MIMO), but we will only use single-input,
single-output (SISO) systems in these tutorials.
To introduce the state space
design method, consider a magnetically suspended ball as shown in the figure below:

The current through the coils induces a magnetic force which can balance the
force of gravity and cause the ball (made of a magnetic material) to be suspended
in midair. The modeling of this system has been established in many control
text books (including Automatic Control Systems by B. C. Kuo, seventh
ed.). The equations for the system are given by:
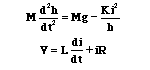
where h is the vertical position of the ball, i is the current through the
electromagnet, V is the applied voltage, M is the mass of the ball, g is gravity,
L is the inductance, R is the resistance, and K is a coefficient that determines
the magnetic force exerted on the ball. For simplicity, we will choose values
M = 0.05 Kg, K = 0.0001, L = 0.01 H, R = 1 Ohm, g = 9.81 m/sec^2 . The system
is at equilibrium (the ball is suspended in midair) whenever h = K i^2/Mg (at
which point dh/dt = 0). We linearize the equations about the point h = 0.01
m (where the nominal current is about 7 amp) and get the state space equations:
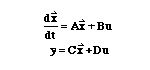
where: 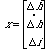 is the set of state
variables for the system (a 3x1 vector), u is the input voltage (delta V), and
y (the output), is delta h.
is the set of state
variables for the system (a 3x1 vector), u is the input voltage (delta V), and
y (the output), is delta h.
Enter the system matrices as:
A = [ 0 1 0
980 0 -2.8
0 0 -100];
B = [0
0
100];
C = [1 0 0];
One of the first things you want to do with the state equations is find the
poles of the system. Recall that the poles are the values of s where det(sI
- A) = 0, or the eigenvalues of the A matrix:
You should get the following three poles:
poles =
31.3050
-31.3050
-100.0000
Note that one of the poles is in the right-half plane, thus the system is unstable in open-loop.
Recall our use of the lsim() Matlab command to simulate systems represented
in transfer function form. Lsim() can also be used to simulate a system represented
in state space form. Let's simulate the open-loop system when the ball is initially
5mm below it's equilibrium point (recall that the first state, x1, is the ball
position relative to equilibrium):
t = 0:0.01:2;
u = 0*t;
x0 = [0.005 0 0];
[y,x] = lsim(A,B,C,0,u,t,x0);
plot(t,y)
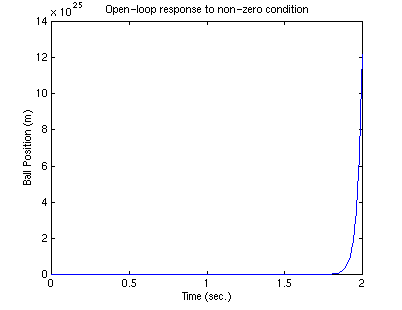
As expected from the RHP pole, the ball displacement blows up over time (of
course it also goes out of the range where our linearization is valid).
Control design using pole placement
While we could certainly use the root locus method to design a feedback system
to position the poles of the closed loop system at some desired location, let's
design a controller for this system using pole placement via state
space methods. As we saw in class, the schematic of a full-state feedback system
is the following:

The term "full state feedback" is used because all states are used
in the feedback system. Recall that the state equation for this feedback system
has the following form:
dx/dt = (A-BK)x + Br
Thus the characteristic polynomial for the closed-loop system is the determinant
of (sI-(A-BK)), i.e. the eigenvalues of (A-BK). Since the matrices A and B*K
are both 3 by 3 matrices, there will be 3 poles for the system. By using full-state
feedback we can place the poles anywhere we want. We will use the Matlab function
place to find the control matrix,
K, which will give the desired poles.
Before attempting this, we have to first decide where we want the closed-loop
poles to be. Suppose the criteria for the controller are:
settling time < 0.5 sec
overshoot < 5%,
This suggests we place the two dominant poles at -10 +/- 10i (at zeta = 0.7
or 45 degrees with sigma = 10 > 4.6*2). However, this is a 3rd order system...where
does the 3rd pole go? Since we don't want this 3rd pole interfering with the
transient response resulting from the dominant poles, let's put the 3rd pole
at least 5x further into the left-half plane than the design points, i.e. p3
= -50. We can change this later depending on what the simulated closed-loop
behavior is. First, define your design poles:
p1 = -10 + 10i;
p2 = -10 - 10i;
p3 = -50;
Now use place() to design the feedback vector K, and lsim() to simulate the resulting
closed-loop system:
K = place(A,B,[p1 p2 p3]);
lsim(A-B*K,B,C,0,u,t,x0);
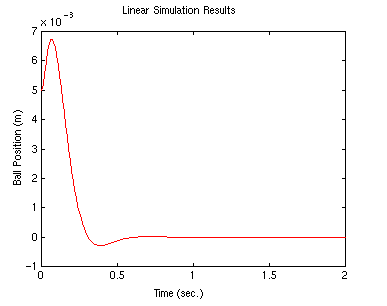
First, note that the overshoot is too large. This is because there are also
zeros in the transfer function which can increase the overshoot; you do not
see the zeros in the state-space formulation. Try placing the poles a bit further
to the left to see if the transient response improves (this should also make
the response faster).
p1 = -20 + 20i;
p2 = -20 - 20i;
p3 = -100;
K = place(A,B,[p1 p2 p3]);
lsim(A-B*K,B,C,0,u,t,x0);
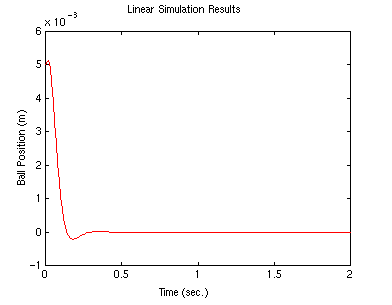
This time the overshoot is greatly improved.
Compare the control effort required (K) in both cases. In general, the
farther you
move the poles, the more control effort it takes.
Note: If you want to place two or more poles at the exact same position, place()
will not work. You can use a function called acker()
which works similarly to place():
K = acker(A,B,[p1 p2 p3])
Introducing the reference input
Now, let's apply a step input u = 0.001m (we choose a small value for the step,
so we remain in the region where our linearization is valid). Replace t,u
and lsim in your m-file with the
following,
t = 0:0.01:2;
u_ss = 0.001; % desired steady-state output of 1mm displacement
u = u_ss * ones(size(t));
lsim(A-B*K,B,C,0,u,t)
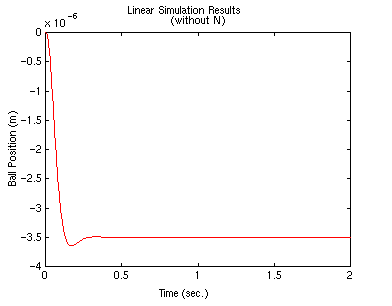
What happened?? The system does not track the step well at all; not only is
the magnitude not one, but it is negative instead of positive.
Recall the schematic of the feedback system, and note that we don't compare
the output to the reference; instead we measure all the states, multiply by
the gain vector K, and then subtract this result from the reference. There is
no reason to expect that K*x will be equal to the desired output. To eliminate
this problem, we can scale the reference input to make it equal to K*x_steadystate.
This scale factor is often called Nbar; it is introduced as shown in the following
schematic:
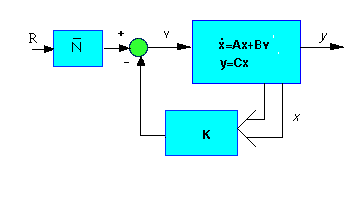
From this schematic, we see that Nbar should be the ratio of the desired displacement
(u_ss = 0.001m) and the steady-state displacement when r(t) = u_ss. There are
several ways to determine Nbar. Since we have not discussed methods for determining
steady-state error from a state space model, let's do this the easy way: look
at your lsim() result above, and determine the steady-state output value of
-3.5E-6
To find the response of the system under state feedback with this introduction
of the reference, we simply note the fact that the input is multiplied by this
new factor, Nbar:
Nbar = u_ss / -3.5e-6
lsim(A-B*K,B*Nbar,C,0,u,t)
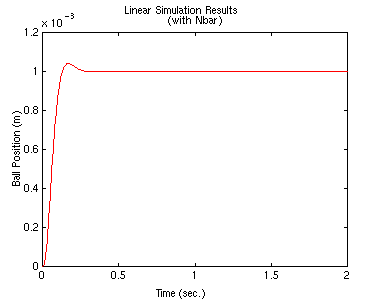
and now the step input is tracked quite well.
Observer design
When we can't measure all the states x (as is commonly the case), we
can build an observer to estimate them, while measuring only
the output y = C x. For the magnetic ball example, we will add three
new, estimated states to the system. The schematic is as follows:
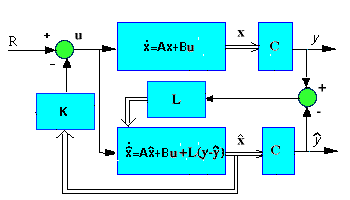
The observer is basically a copy of the plant; it has the same input and
almost the same differential equation. An extra term
compares the actual measured output y to the estimated output 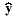 ; this
will cause the estimated states
; this
will cause the estimated states 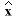 to approach the values of the
actual states x. The error dynamics of the observer are given by the poles of
(A-L*C).
to approach the values of the
actual states x. The error dynamics of the observer are given by the poles of
(A-L*C).
First we need to choose the observer gain L. Since we want the
dynamics of the
observer to be much faster than the system itself, we
need to place the poles at least five times farther to the left than the
dominant
poles of the system. If we want to use place(), we need
to put the three observer poles at different locations.
op1 = -100;
op2 = -101;
op3 = -102;
Because of the duality between controllability and observability, we can
use the
same technique used to find the control matrix, but replacing the
matrix B by the matrix C and taking the transposes of each matrix (consult
your text book for the derivation):
L = place(A',C',[op1 op2 op3])';
The equations in the block diagram above are given for 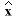 . It is
conventional to write the combined equations for the system plus observer
using the original state x plus the error state: e = x -
. It is
conventional to write the combined equations for the system plus observer
using the original state x plus the error state: e = x - 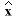 .
We use as state feedback u = -K
.
We use as state feedback u = -K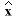 . After
a little bit of algebra (consult your textbook for more details), we arrive at
the combined state and error equations with the full-state feedback and an
observer:
. After
a little bit of algebra (consult your textbook for more details), we arrive at
the combined state and error equations with the full-state feedback and an
observer:
At = [A - B*K B*K
zeros(size(A)) A - L*C];
Bt = [ B*Nbar
zeros(size(B))];
Ct = [ C zeros(size(C))];
To see how the response looks to a nonzero initial condition
with no reference input, add the following lines into your m-file. We
typically assume that the observer begins with zero initial condition,
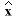 =0. This gives us that the initial condition for the error
is equal to the initial condition of the state.
=0. This gives us that the initial condition for the error
is equal to the initial condition of the state.
lsim(At,Bt,Ct,0,zeros(size(t)),t,[x0 x0])
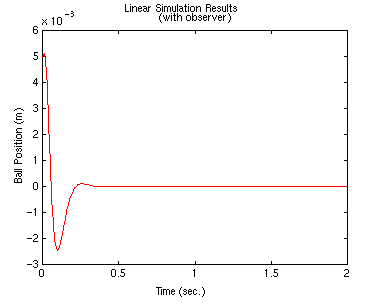
Responses of all the states are plotted below. Recall that lsim gives us x
and e; to get 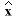 we need to compute x-e.
we need to compute x-e.
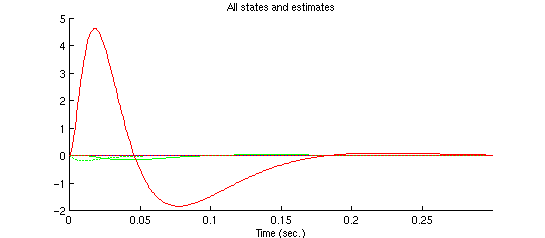 Zoom in to see some detail:
Zoom in to see some detail:
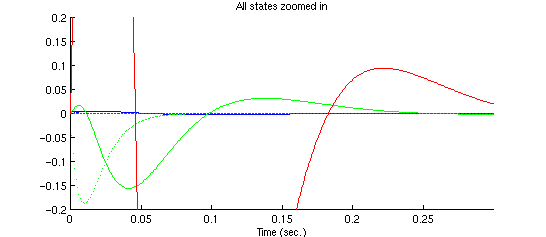
The blue solid line is the response of the ball position 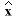 , the
blue dotted line is the estimated state
, the
blue dotted line is the estimated state 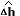 ;
;
The green solid line is the response of the ball speed 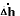 , the
green dotted line is the estimated state
, the
green dotted line is the estimated state 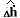 ;
;
The red solid line is the response of the current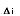 , the red dotted
line is the estimated state
, the red dotted
line is the estimated state 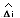 .
.
We can see that the observer estimates the states quickly
and tracks the states reasonably well in the
steady-state.
The plot above can be obtained by using the plot command.
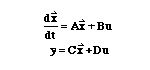

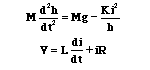
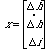 is the set of state
variables for the system (a 3x1 vector), u is the input voltage (delta V), and
y (the output), is delta h.
is the set of state
variables for the system (a 3x1 vector), u is the input voltage (delta V), and
y (the output), is delta h. 







 ; this
will cause the estimated states
; this
will cause the estimated states  to approach the values of the
actual states x. The error dynamics of the observer are given by the poles of
(A-L*C).
to approach the values of the
actual states x. The error dynamics of the observer are given by the poles of
(A-L*C).


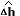 ;
; 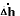 , the
green dotted line is the estimated state
, the
green dotted line is the estimated state 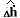 ;
; 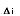 , the red dotted
line is the estimated state
, the red dotted
line is the estimated state 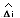 .
.