CTM Example: DC Motor Speed Modeling

DC Motor Speed Modeling

ENME462

A common and very important actuator in control systems is the DC motor. It directly provides rotary motion and, coupled with wheels or drums and cables, can provide transitional motion. The basic electric circuit of the armature and the free body diagram of the rotor are shown in the following figure:

For this example, we will use the following values for the physical parameters:

moment of inertia of the rotor (J) = 0.01 kg.m^2/s^2
damping ratio of the mechanical system (b) = 0.1 Nms
electromotive force constant (K=Ke=Kt) = 0.01 Nm/Amp
electric resistance (R) = 1 ohm
electric inductance (L) = 0.5 H
input (V): Source Voltage
output (theta): position of shaft
The rotor and shaft are assumed to be rigid

The motor torque, T, is related to the armature current, i, by a constant factor Kt. The back emf, e, is related to the rotational velocity by the following equations:

In SI units (which we will use), Kt (armature constant) is equal to Ke (motor constant).

From the figure above we can write the following equations based on Newton's law combined with Kirchhoff's law:

Using Laplace Transforms, the above modeling equations can be expressed in terms of s.

By eliminating I(s) we can get the following open-loop transfer function, where the rotational speed is the output and the voltage is the input.

Design requirements

Since one of the most basic requirements of a motor is that it should rotate at the desired speed, the steady-state error of the motor speed should be less than 1%. In this case we would like to achieve a rotational speed of 1 rad/sec. Another performance requirement is that the motor must accelerate to its steady-state speed quickly after being turned on. In this case, we want it to have a settling time of 0.5 sec. Finally, since a speed faster than the reference may damage the equipment, we want to limit the overshoot to 5% or less. Thus, for a reference input r(t) = u(t), the motor speed output should have:

target speed = 1 rad/sec for 1 V applied voltage
Ts < 0.5 sec
%OS < 5%
ess < 1%

Open-loop response

We can represent the above transfer function within Matlab by defining the numerator and denominator matrices as follows:

Create a new m-file and enter the following commands:

J=0.01;
b=0.1;
K=0.01;
R=1;
L=0.5;
num=K;
den=[(J*L) ((J*R)+(L*b)) ((b*R)+K^2)];
G = tf(num,den);

Now let's see how the original open-loop system performs. Add the following commands onto the end of your m-file and run it in the Matlab command window:

step(G)
title('Step Response for the Open Loop System')

You should get the following plot:

From the plot we see that when 1 V is applied to the system, the motor can only achieve a maximum speed of 0.1 rad/sec, ten times smaller than our desired speed. Also, it takes the motor 3 seconds to reach its steady-state speed; this does not satisfy our 0.5 seconds settling time criterion. Clearly we cannot achieve our design goals using open-loop control.

Recall that we want to control motor speed, Ts, %OS, and ess. One approach would be to place a voltage amplifier with a gain of K in front of the open loop system. If a large enough gain was used, we could increase the output speed to reach the target speed. However, as we learned in lecture, such an open-loop control approach will not allow us to affect %OS, Ts, or ess. A closed-loop controller is needed.

Closed-loop response

Feedback can be used to modify both transient and steady-state performance of a closed-loop system. Although we have not covered specific methods for control system design (coming soon), we can use this motor example to see what happens when we add a simple closed loop around the plant. Specifically, we will perform proportional control here. Proportional control is one way to modify the transient performance of a system. In essence we will add controller with a transfer function K (simple gain) in series with the plant, and place a unity-gain negative feedback loop around KG(s).

Keep in mind that G(s) is the transfer function between input voltage and motor speed. For this example, we will use motor speed as the controlled system output c(t), and apply a reference input r(t) which is the desired motor speed d(theta)/dt. The block diagram looks like this:

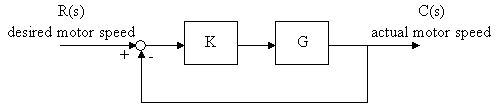
Use MatLab to define the closed-loop transfer function for this block diagram. You can either derive an analytical expression for T(s), or use MatLab's feedback() function to do this for you, with the following syntax:

feedback(G,H)

where G and H are sys objects. This command will produce the closed loop transfer function for a negative feedback system with forward path transfer function G(s) and feedback path transfer function H(s). Negative feedback is assumed. If positive feedback is desired, use feedback(G,H,+1).

For the closed-loop motor system, find T(s) for the case where K=10 and plot the step response:

K = 10;
T = feedback(K*G, 1)
step(T)

Note that we have increased the amplitude by a factor of 5, and are now only at 50% (rather than 10%) of our target value. More importantly, the settling time is improved by a factor of about 3: we are now much closer to the desired performance specification of Ts < 0.5 sec. Note that %OS remains within the specifications, since the feedback has not induced any overshoot.

Assignment:

1. Hand in printouts of all work for the above example (m-files and plots).

2. Play around with changing the value of K. Can you find a K that will simultaneously meet all performance specs?

3. By increasing the value of K, all specs can be improved. What is the cost of doing this? In other words, is there a practical reason that we may not be able to select an arbitrarily large value of K? Explain.