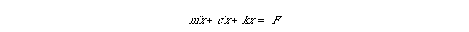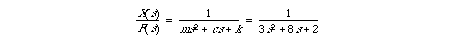ENME462
Studio 3
MatLab System Modeling
-
tf()
-
tfdata()
-
roots()
-
tf2zp()
-
zp2tf()
-
poly()
-
residue()
-
impulse()
-
step()
-
lsim()
- pole()
- zero()
- pzmap()
A. Overview of the MatLab Control System Toolbox
MatLab offers a special toolbox for analyzing control systems called (surprise!)
the Control System Toolbox. To see the various commands provided by this toolbox,
type the command:
A simple demonstration of some of the features of this toolbox
can be seen by running the command:
Run this command and you will be rewarded with a number of plots
that may not mean much to you yet. That's ok, we'll get there soon.
In version 5 of MatLab, many of the functions in the control
toolbox require a special data object called a system, or SYS. A SYS object
is an internal MatLab representation of an LTI (linear time invariant) dynamical
system. A SYS object may be created in several ways. In this studio we will
focus on creating system objects from transfer function polynomials using
the tf command.
(NOTE: COMMANDS CAMPATIBLE WITH MATLAB
VERSION 4 ARE DISCUSSED FOR THOSE WHO WANT TO USE PRE-v5 AT HOME. IN GENERAL,
COMMANDS WHICH REQUIRE A SYS DATA OBJECT IN v5 CAN BE USED IN MATLAB v4 BY
PASSING (num, den) INSTEAD OF (sys) TO THOSE FUNCTIONS.)
B. Model Creation via tf()
This section only applies to MatLab
version 5, since earlier versions do not support the SYS data object.
Recall that transfer functions provide a convenient way of
expressing the relationship between the input and output of a linear system
when all initial conditions are zero. The roots of the numerator of a transfer
function are called the zeros of the system, and the roots of the denominator
are called the poles of the system.
Consider a simple mechanical spring-mass-damper system:
Assuming zero initial conditions, a free body diagram of
this system results in the following differential equation of motion:
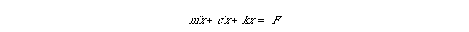
Taking the Laplace transform of this equation and solving for the transfer
function X(s) / F(s) results in:
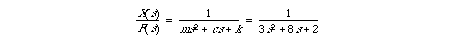
Let's define the numerator and denominator of the transfer function separately
(you'll see why soon). The numerator is simply a scalar. At the MatLab
prompt, type:
The denominator is a little trickier, since it is a polynomial
of the Laplace variable s. In MatLab, a polynomial is represented as a row
vector containing the polynomial coefficients in descending order. For example,
the polynomial 2s3 + s + 5 would be represented by the vector [2, 0, 1,
5]. For the current problem, the denominator polynomial is 3s2 + 8s + 2.
To define the polynomial in MatLab, type:
Now that we have defined the numerator and denominator of
the transfer function, a SYS data object for the spring-damper system can
be created, using the tf() function. To define
the SYS data object for this system (let's call it
sys ), type:
MatLab should respond by showing the transfer function of
the system. We now have a variable sys which
can be used to analyze the spring-mass-damper system. Unfortunately, not
all MatLab functions are able to take a SYS object as an argument. For these
functions, we will have to describe the system by its numerator and denominator
polynomials instead.
Once you have a SYS object, the original numerator and denominator
of the system can be recovered using the tfdata()
function. Try typing:
[num, den] = tfdata(sys,'v')
MatLab shouold respond by displaying the original numerator
and denominator.
C. Poles and zeros
A transfer function can be described by its poles (roots of the denominator)
and zeros (roots of the numerator). The roots()
function can be used to find the roots of a polynomial. To find the zeros
and poles of our example system, type:
zeros = roots(num)
poles = roots(den)
Alternately, the zeros and poles may be found simultaneously
using the tf2zp() function, where
tf2zp stands for "transfer function to zeros & poles".
To do this, type:
[zeros2, poles2] = tf2zp(num, den)
You should find that zeros and
poles are the same as zeros2 and
poles2 . In both cases, you should find there are no finite zeros, and
the poles are located at s = -2.3874 and s = -0.2792.
Another useful MatLab function, called
zp2tf() , can be used to define a transfer function from a set of poles
and zeros. In this case, the arguments of the function are the poles and zeros
placed in row vector form, and the result of the function is 2 vectors containing
the numerator and denominator polynomials. For example, the poles of our example
are located at s = -2.3874 and s = -0.2792, and there are no finite zeros.
To find the transfer function given this information, type:
[num2, den2] = zp2tf([], [-2.3874, -2.3874], 1/3)
Which should return the following:
num2 = 0 0 0.3 333
den2 = 1.0000 2.6 666 0.6666
The third argument of the zp2tf()
function is the scalar gain of the transfer function. Why is this needed?
Given a set of poles, there are an infinite number of polynomials which have
those poles as their roots; if we find one such polynomial, then any scalar
multiple of that polynomial will possess the same roots. When you give MatLab
a set of zeros and poles, it chooses polynomials for the numerator and denominator
which are scaled so that the highest order coefficient of each polynomial
is equal to one. In order to produce the desired transfer function, you need
to tell MatLab what the scalar gain should be based on this fact. For our
example system, a scalar gain of 1/3 is used since, by observation of the
original transfer function, we would need to divide both the numerator and
denominator through by 3 to produce numerator and denominator polynomials
with the highest order coefficient of each polynomial equal to one.
A final way to go between a transfer function representation
of a system and a pole/zero representation is to use the
poly() function. This is the inverse of the
roots() function, but now we provide the roots of a polynomial as arguments
to the function (in vector form), and the result of the function is a polynomial
which possesses those roots. Just as with zp2tf()
, poly( ) returns a polynomial with a highest-order
coefficient of one. Using our previously defined variables, type:
num3 = poly(zeros)
den3 = poly(poles)
These commands will produce the following output:
num3 = 1
den3 = 1.0000 2.6667 0.666
To produce the original transfer function, a scalar value of
1/3 must be multiplied on the numerator. This is analogous to including the
scalar gain of 1/3 to the zp2tf() function.
Another way of finding poles of a system, along with the zeros,
is by using Matlab's pole(), zero(), and pzmap()
functions. Each of these functions works on a SYS data type. Use
the help command for more info on these functions. You will use them
in the assignment at the end of this lab.
D. Partial Fraction Expansion and Residues
MatLab can also be used to perform partial fraction expansion of transfer
function expressions. This can be very handy for examining the response of
individual components of a larger transfer function. First, verify that you
still have the original numerator and denominator polynomials,
num and den , properly defined. To perform
a partial fraction expansion on this transfer function, type:
[R, P, K] = residue(num, den)
R is a vector containing the residues,
P is a vector containing the component poles, and
K is sometimes called the
direct term .
The residue() function breaks
the transfer function defined by num and
den into its n component residues, where
n is the order of the denominator:
num(s) R(1) R(2) R(n)
------ = -------- + -------- + ... + -------- + K(s)
den(s) s - P(1) s - P(2) s - P(n)
If the order of the denominator is larger than the
order of the numerator, then K will be zero (can you explain why?)
E. Impulse response
Now that you know how to create SYS data objects and represent
systems in terms of transfer functions and poles/zeros, we can look at the
time response of linear systems. In this studio we'll consider the response
of a linear system to two types of inputs: impulse and step functions.
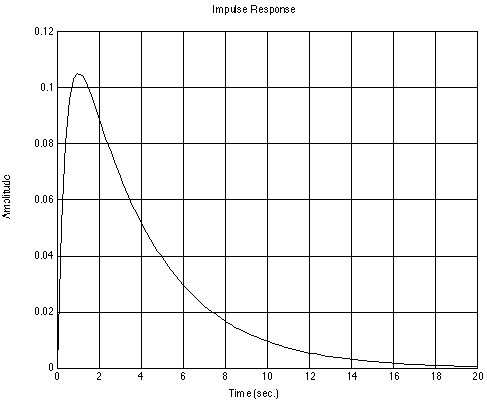
The impulse response of an LTI system can be plotted using the
impulse() function. To try this with our example
system, type:
impulse(sys)
recall that in Matlab v4, you need to replace the 'sys' object with 'num,den',
i.e.:
impulse(num,den)
The output should look like:
Note: you won't see the grid lines unless you execute the "grid" command
after making the impulse plot
This plot shows the time response of the mass when a unit impulse force
is applied to the mass at time t=0s. If you want to see the response for
a longer period of time, the impulse() function
will also take a time vector as an argument. Try this:
impulse(sys, [0 : 0.1 : 40])
You should get the same basic plot as before, but with a 40s
time axis.
Note that instead of using the SYS data object as input to
the function, we could also have used the numerator and denominator polynomials,
num and den , defined
earlier. In general, it is better to stick with using SYS, since some MatLab
functions will require this, and future versions of MatLab may require it
for all control toolbox functions (get used to
it now!).
In some cases, getting a pretty plot isn't enough. Instead,
you may want the actual numbers for the mass position as well as the associated
time vector. To get this information, type:
Make sure you type the semicolon at the end of the first line,
or else the entire output and time vectors will be displayed on the screen.
The values describing the position of the mass are now held in
x , and the corresponding values of time are held in
t .
F. Step response
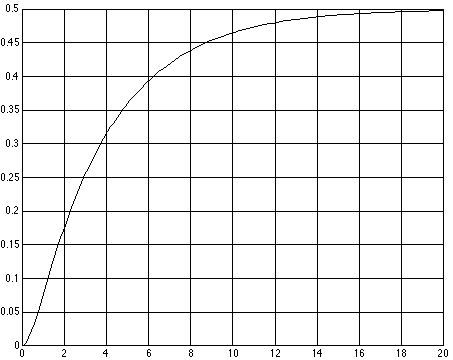
Step response can be found using MatLab's step()
function, which operates the same way as impulse().
In this case, the forcing function is a unit step applied at time t=0s.
To plot the step response of our system, type:
step(sys)
[x, t] = step(sys)
plot(t,x)
After typing the plot command, you should see the following:
The x-axis corresponds to the time vector returned by [x, t] = step(sys), and
the y-axis shows the response vector, x(t).
If a longer time period is desired in the plot, say t = 0 to 50 sec, you can
create the required time vector as:
t = [0 : 0.2: 50];
and then pass this vector to the step() function:
x = step(sys, t)
or
x = step(num, den, t)
G. General linear simulation
A more general technique for simulating the response of a linear system to
an arbitrary input signal is the lsim() function.
To see how this function works, say we want to simulate the response of our
system to a function F(t) = 1 for t<10s, F(t) = 0 for t>10s. First, generate
a time vector containing the time points of interest, say for 0 < t < 20s
in 0.1s increments:
t = [0:.1:20];
Next, create an input vector F where the ith element of the vector contains
the value of F(ti), and ti is the value contained in the ith element of the
time vector:
F = zeros(size(t));
F(1:(length(t)+1)/2) = ones((size(t)+1)/2);
If you don't fully understand the syntax of setting up the forcing function,
don't worry about it too much. With more experience using MatLab this sort of
expression will become second nature to you. To plot the response of the system
to this input, type:
x = lsim(sys, F, t);
As you can see, lsim() takes a
SYS , input F , and time
t as arguments, and returns the output x . This
is a very powerful function which allows you to simulate any arbitrary input
function you might want to investigate.
H. Time response of 2nd order systems
Let us briefly consider the response of second order systems. You are given
the following second order (open-loop) system whose transfer function is:
1 G(s)
R(s)= --- _______________
s | b | C(s)
-------------| ------------ |--------->
|s^2 + a s + b |
---------------
Depending on the pole locations, the system is either overdamped, critically
damped, underdamped, or undamped. The following examples illustrate the different
cases:
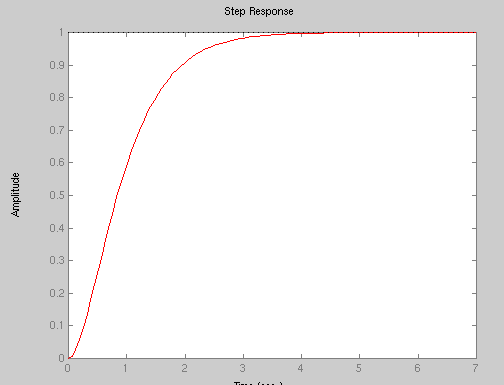
(1) Overdamped
4
G(s) = ------------ (1)
s^2 + 5 s +4
Create the system in Matlab and apply the step() function. The step response
of system (1) is
(2) Critically damped
4
G(s) = ------------ (4)
s^2 +4 s + 4
Create the system in Matlab and apply the step() function. The step response
of system (4) is
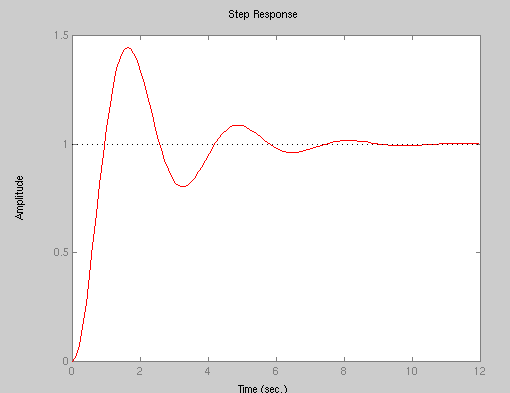
(3) Underdamped
4
G(s) = ------------ (2)
s^2 + s +4
Create the system in Matlab and apply the step() function. The step response
of system (2) is
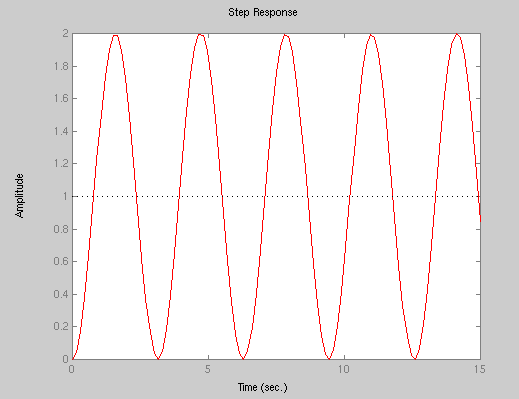
(4) Undamped
4
G(s) = ------------ (3)
s^2 + 4
The step response of system (3) is
We will shortly be working with 2nd order systems in lecture. Understanding
the relationship between pole locations and dynamic behavior of 2nd order
systems is important for many control problems.
Assignments
1. For the above four cases, do the following:
a. create each system in Matlab and apply the step() function
to plot the step response.
b. calculate the poles of the plants (use the MatLab roots()
or pole() function).
c. use MatLab to plot the pole/zero locations of each plant (use the
pzmap() function)
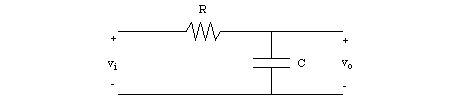
2. Derive the transfer function of the following electrical
network by hand. The input is the voltage vi(t)
and the output is the voltage vo(t) .
3. Write a MatLab m-file which will do the following (turn in
m-file and output file including all plots)
a. Calculate the poles and zeros of the transfer function
G = Vo/Vi
b. Use these poles and zeros to represent the transfer function
within MatLab. Don't forget the scaling factor!
c. Re-represent the system in MatLab by entering the numerator
and denominator polynomials. Check that the results agree with 5(b).
d. Plot the impulse response of the system.
e. Plot the response to an input voltage of vi(t) = 2V, i.e.
a scaled step input voltage.
f. Use lsim() to plot the response to an input defined by:
vi(t) = 3V for 0s < t < 9s
vi(t) = 0V for 9s < t