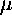 , r2 = -i
, r2 = -i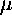 with nonzero
with nonzero 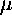
There is an error in Boyce/diPrima in table 9.3.1 on page 484 about types of critical points of almost linear systems:
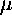 , r2 = -i
, r2 = -i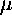 with nonzero
with nonzero 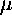
In these cases even very near the critical point the trajectories of the nonlinear system can be very different from those of the linear system.
Here is a correct table. One can construct examples where ``other'' types than the ones in table 9.3.1 occur.