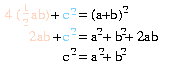with one angle right.
Construct three more just like it,
all equal by sight.
Arrange them into a square,
long sides in middle,
shorter sides on the outside,
long next to little.
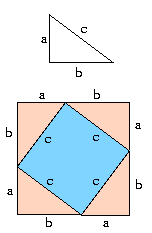
is sum of the parts,
so the triangle and square
which long sides demark
are equal in area
to the square outside.
Thus yielding the conclusion
which can't be denied
that the hypot'nuse's length,
upon being squared,
equals the sum of squared lengths
of the shorter pair.