Fundamentally, the LE4PD is a modified Rouse-Zimm approach to modeling protein dynamics that accounts for residue-specific friction coefficients, long-ranged hydrodynamic interactions between residues in the protein, and a protein-specific potential of mean force between residues that is built using informaton from atomistic molecular dynamics simulations. The coupled equations of motion for the coarse-grained sites (the alpha-carbons) in real space are subject to a linear transformation to yield a set of uncoupled equations of motion in a mode space of the same dimensionality, although typically the first ten or modes are those where most of the focus is applied, as they correspond to the most slowly decaying modes in the system. However, the behavior of all the modes must be taken into account accurately to describe faithfully e.g. time correlation functions where the dynamics are mapped back to the real space from the mode space. But performing a functional analysis of the dynamics in the mode space is absolutely critical for interpreting the functional behavior of the protein.
Fundamentally, in the mode space, as well as in the real space, the equation of motion of the modes is governed by an overdamped Langevin equation, where the force acting on each mode or bead is dictated by a combination the hydrodynamics and the correlations between the bond vectors defined between adjacent beads in the protein. Overall, the interactions between the beads in the protein are modelled as entropic springs with the beads also subject to the random impacts of the solvent governed by the random noise term in the Langevin equation and the associated fluctuation dissipation theorem.
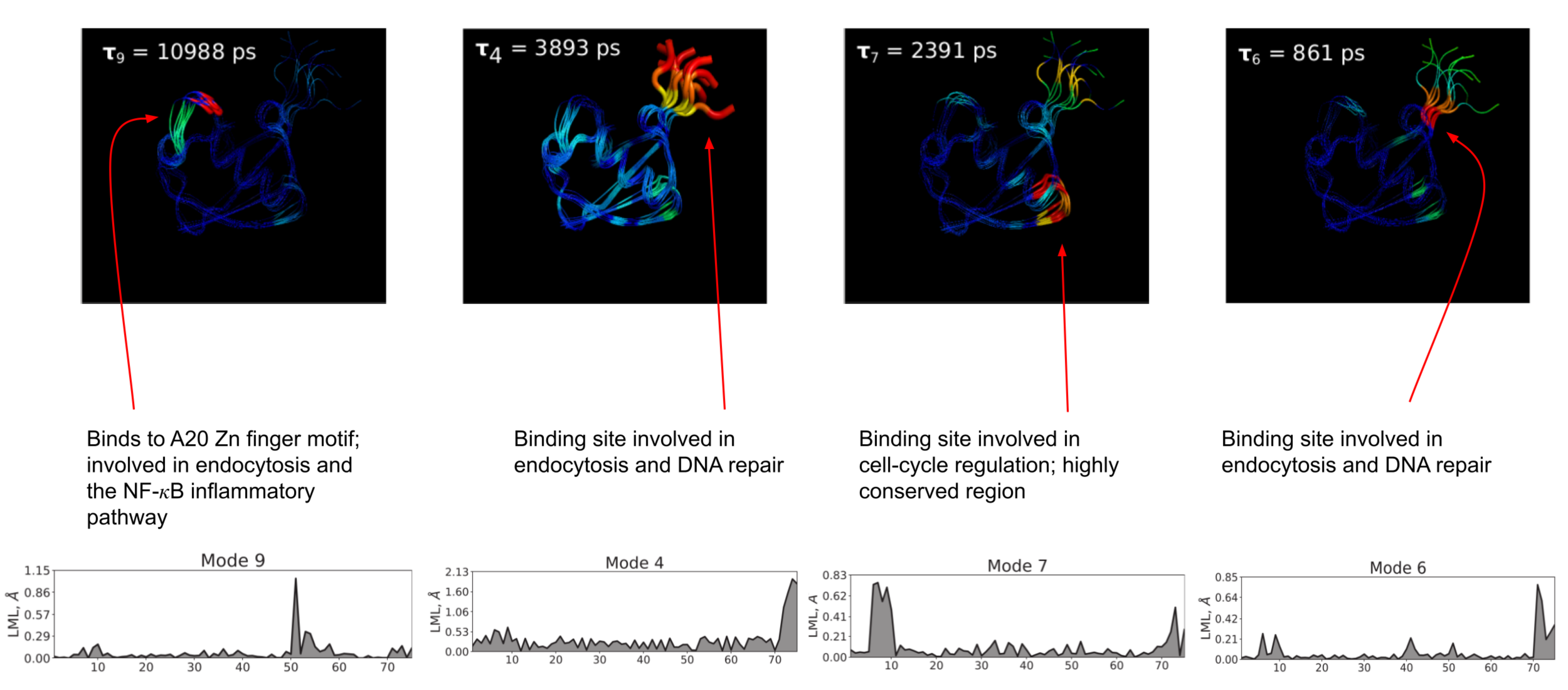
However, since the model is both coarse-grained at the alpha-carbon level and the springs between beads are assumed to be harmonic, we must account for free-energy barriers along the mode coordinates in some manner if we want to correctly account for the timescales of the important dynamics of the protein. To take account of barriers, we take inspiration from Zwanzig's diffusion in a rough protential model and calculate the relevant free-energy barrier along each mode, using it to effectively renormalize the diffusion coefficient along that mode. Previously, the barriers were found by approximating a characteristic roughness of the free-erngy surface. I took a slightly more precise approach by approximately the slowest dynamics on the first ten modes of ubiquitin using a discrete-state kinetic model known as a Markov state model (MSM). We assume that the slowest modes in the system are slow enough to be ammenable to the MSM formulation and that all faster modes, since they cannot be described using the MSM approach, do not possess metastable minima, and, hence, their free-energy landscapes are merely rough, without any significant energy barriers impeding transport. Since the landscapes for the faster modes are merely rough, we can use the previous heuristic for these modes while treating the kinetics of the slow modes carefully through the MSM construction. This approach allowed for a better interpretation of the slow moded space, and we are able to postulate how these slow mode dynamics are related to the functional dynamics of ubiquitin.

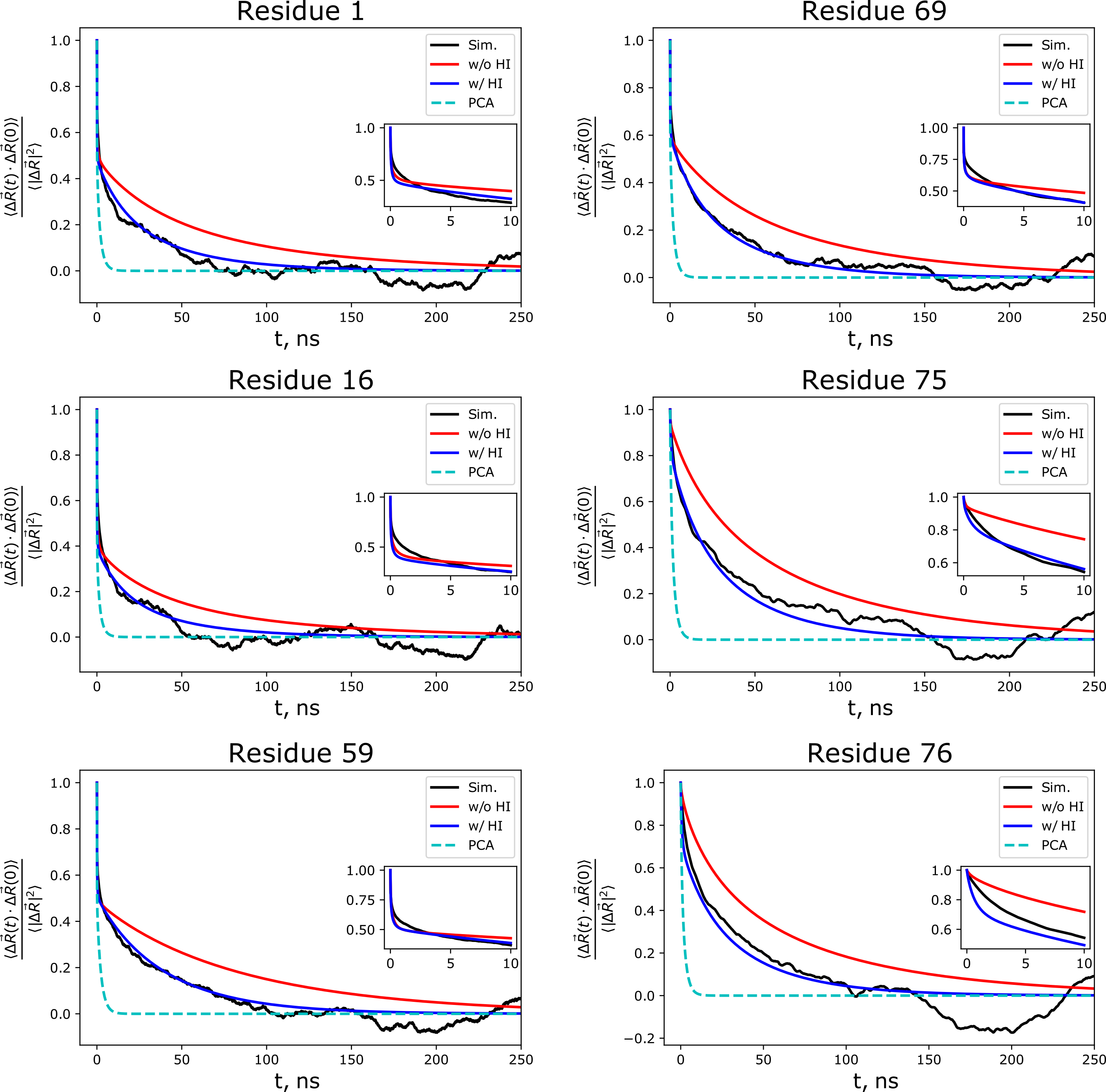
This MSM technique can also be combined with the anisotropic version of the LE4PD mentioned above to create the LE4PD-3N approach to modelling protein dynamics. With the LE4PD-3N, we shift from the simulation box frame of reference to the body-centered frame of reference, which removes rotational and translational motions from the system, yielding a set of 3N-6 internal modes of motion. As with the isotropic LE4PD, once rescaling due to the free-energy barriers along each of the mode coordinates, the lowest index modes give the slowest internal dynamics of the protein. Due to the analytical mapping onto the PCA in alpha-carbon coordinates, we are able to show the importance of hydrodynamic effects and free-energy barriers to the predicted slow dynamical motions of the proteins, including the improved ability of the LE4PD-3N to reproduce the simulated time correlation functions from the simulation trajectory.
The study comparing the LE4PD-3N method with PCA for modeling the dynamics of ubiquitin was followed up by a study comparing the results of the LE4PD-3N method to the time-lagged extension of PCA, tICA. We performed a detailed comparison of the predicted slow mode dynamics and kinetics between the two approaches and found that the LE4PD-3N is slightly more robust at predicting the dynamics due to its lack of the lagtime parameter present in tICA. However, if the lagtime in tICA is tuned precisely, it can do very well at predicting the decay of the autocorrelation function in regions of the protein undergoing the slowest dynamical transitions.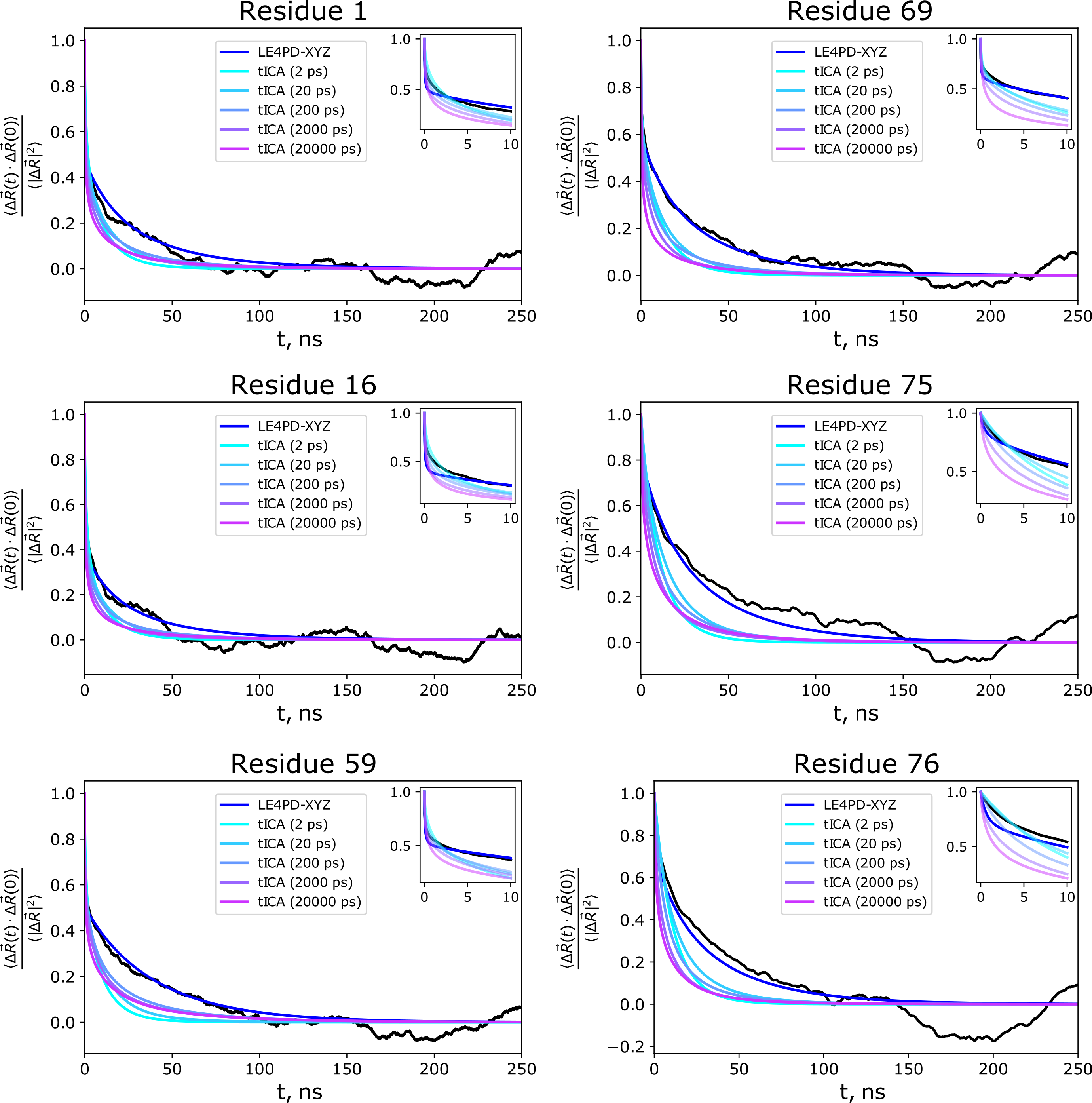
As another application of MSMs to biological systems, we performed long (1 microsecond) simulations of deoxyadenosine dinucleotide (dApdA) in aqueous solution of varying NaCl concentration. The free-energy landscape of the dApdA molecule projected in the two-dimensional space of the radial separation between the nucleobases and the twist angle around this axis was used to as the reduced state space for construction of an MSM that was subsequently coarse-grained using the robust Perron cluster-cluster analysis (PCCA+) method. The coarse grained transition matrix dedscribing the conditional transition probabilites among these coarse-grained macrostates was used to interpret the unstacking mechanism as well as its associated timescale. We find that each macrostate defines a physically relevant set of conformations, e.g. right-handed structures, left-handed structures, unstacked, stacked and achiral. The structural statistics in each macrostate was combined with Schellman's matrix method to calculate the circular dichroism (CD) spectra for each macrostate. We found that, in agreement with prior conjectures, that the CD spectrum is due almost exclusively to a linear combination of two states. However, in contrast to that conjecture, we found that the CD spewctrum is due mostly to the predominant left- and right-handed states, not a right-handed and unstacked state. Using the average CD from this state gave very similar results to using just the average structure from each macrostate. Thus, we provided a computationally convenient method to extract the relevant metastable states, a determination of how the conformational diversity of dApdA contributes to its CD spectrum, and postulate a mechanism, including the associated kinetics, for the unstacking transition of this simple nucleic acid system.
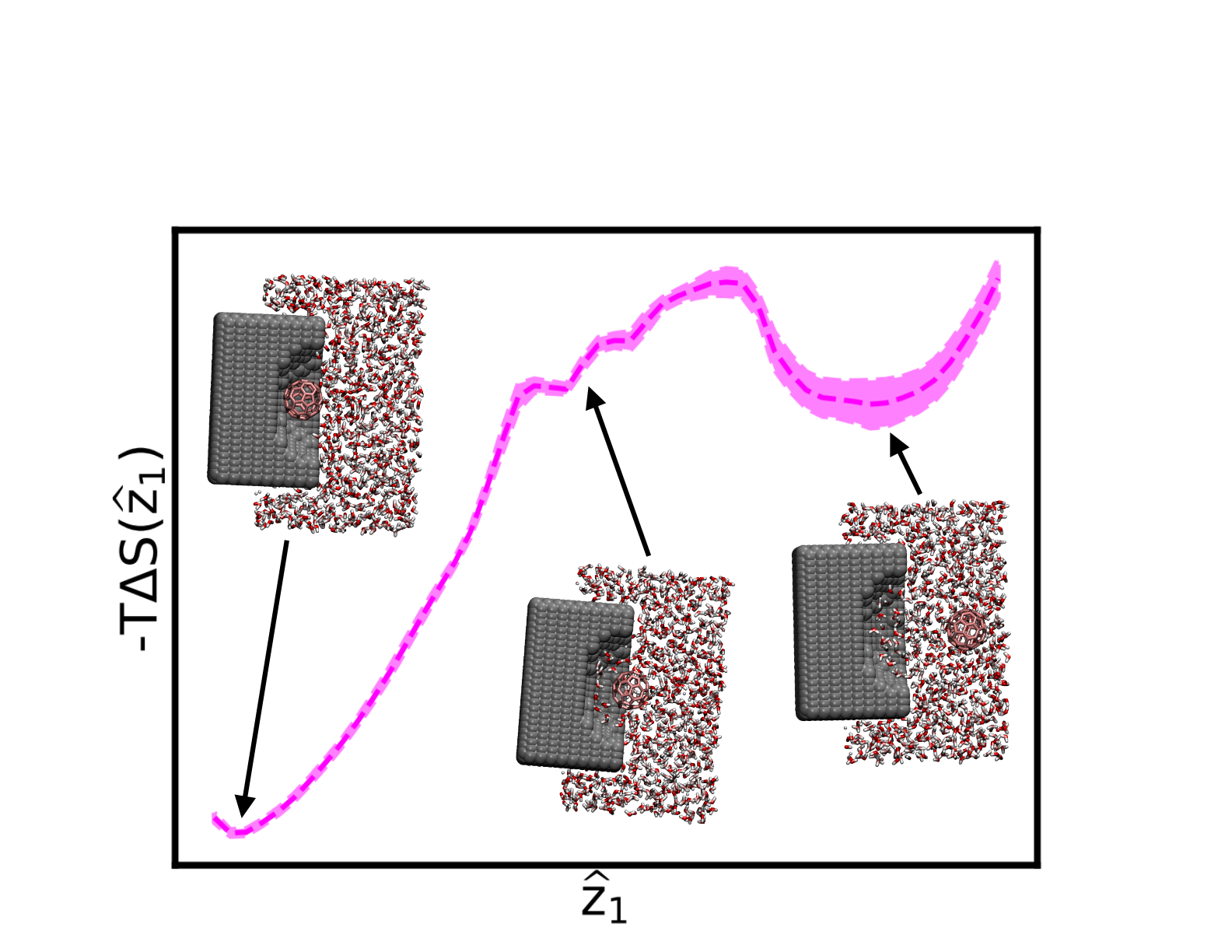
While I have studied some nucleation phenomena while at UMD, my focus to date has been on calculating the thermodynamic profiles of RCs learned using the SPIB approach. One of my recent projects has focused on determining good RCs for the unbinding of two model hydrophobic ligands, a united-atom methane particle and a C60 buckyball fullerene, from rigid, hydrophobic pockets. From this analysis, we confirm that a thermodynamically-optimized, one-dimensional RC for the unbinding for both the methane and buckyball involves surmounting an entropy barrier to unbind, with energetic considerations playing a minor role. Furthermore, we find that solute wetness is the main driver of methane dissociation while pocket wetness plays a major role for the buckyball system until the transition state, after which solute wetness dominates the RC. These observations should yield transferable knowledge to the important features describing ligand unbinding in more complication and physiologically relevant systems, such as drug-protein interactions. This study is published in the Journal of Physical Chemistry B. A preprint is available on the arXiv.