



Anil Deane/UMCP
Paul Fischer/ANL
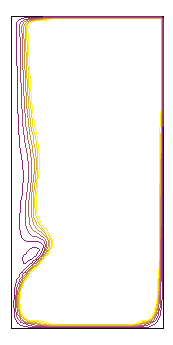
Full Rod Scenario. Co-rotating rod.
 |
 |
 |
 |
 |
| omega_rod = 0 | 2 | 5 | 10 | 15 |
Figure1. Shows contours that as a full rod is rotated at increasing rates the vortex bubble is eliminated. However note that a new bubble at the top (near the lid) appears.
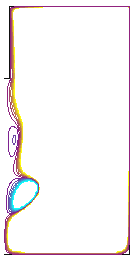
Top Short Rod Scenario. Co-rotating rod.
 |
 |
 |
 |
 |
|
|
|
|
|
|
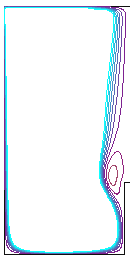
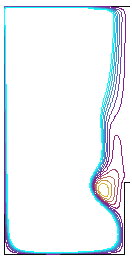
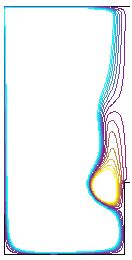
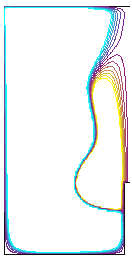
Bottom Short Rod Scenario. Co-rotating rod.
 (a) (a) |
 (b) (b) |
 (c) (c) |
 (d) (d) |
|
|
|
|
|
Figure 3. Shows that a co-rotating rod at the bottom, with extent close to that of the bubble increases the bubble size as the rotation rate is increased. Note the presence of the short rod modifies the bubble shape and size of the bubble from the no-rod and the full-rod cases.
Bottom Short Rod Scenario. Counter-rotating rod.
 |
 |
 |
|
|
|
|
Figure 4. Shows that a counter-rotating rod at the bottom, fails to supress the bubble and causes unsteadiness as the rotation rate is increased.

Anil Deane, Laboratory for Computation and Visualization
Institute for Physical Science and Technology