[December 3, 2002]
Biological Sciences:
Neuroscience
GLOBAL
OPTIMIZATION OF CEREBRAL CORTEX LAYOUT
Christopher Cherniak*‡, Zekeria Mokhtarzada*,
Raul Rodriguez-Esteban*, B. K. Changizi†
*Committee for Philosophy and the Sciences, Department of Philosophy, University of Maryland, College Park, MD 20742.
†Huntington Memorial Hospital, 100 West California Boulevard, Pasadena, CA 91109.
‡To whom reprint requests should be addressed. cherniak@umd.edu
Corresponding author: Christopher Cherniak, 301-405-5704 [lab], 301-405-5690 [fax], cherniak@umd.edu
[See
also supplementary material: University
of Maryland Institute for Advanced Computer Studies Technical Report
UMIACS-2003-103.
www.cs.umd.edu/Library/TRs/CS-TR-4535/CS-TR-4535.pdf ]
GLOBAL
OPTIMIZATION OF CEREBRAL CORTEX LAYOUT
Christopher Cherniak, Zekeria Mokhtarzada,
Raul Rodriguez-Esteban, B. K. Changizi
Functional
areas of mammalian cerebral cortex seem positioned to minimize finely costs of their
interconnections, down to a best-in-a-billion optimality level. The optimization problem here, originating
in microcircuit design, is: Given
connections among components, what is the physical placement of the components
on a surface that minimizes total length of connections? Because of unfeasibility of measuring
longrange “wirelength” in the cortex, a simpler adjacency cost was validated. To deal with incomplete information on brain
networks, a Size Law was developed that predicts optimization patterns in
subnetworks. Macaque and cat cortex
rank better in this connection optimization than the wiring of comparably
structured computer chips, but somewhat worse than the macroeconomic
commodity-flow network among U.S. states.
However, cortex wiring conforms to the Size Law better than the
macroeconomic patterns, which may indicate cortex optimizing mechanisms involve
more global processes.
Simple "Save
wire" generative principles from combinatorial network optimization theory
predict layout of sensory areas of macaque and of cat cerebral cortex.
The areas appear to be positioned on the cortex to minimize interconnecting
wiring, in some cases to current limits of detectability.
This picture of large-scale component placement optimization in the
cortex resembles earlier findings for ganglion layout in the nervous system
of Caenorhabditis elegans (1, 2),
and for optimization of neuron arbors (3, 4),
but to orders of magnitude finer optimality (5, 6).
Computer searches of all of the tens of millions of alternative possible
roundworm ganglion placements had indicated that the actual layout of the nematode
requires the least total wirelength for the nervous system's one thousand
connections. On the model of these
worm ganglion searches, we have worked out methods for optimality searches
of layouts of cerebral cortex areas: To
avoid difficulties of wirelength measurement, a more manageable adjacency
cost was calibrated as a surrogate. To
detect optimization of subnetworks when the complete network is inacessible,
and to distinguish local from larger-scale optimization mechanisms, a Size
Law was articulated (7).
We present evidence that the cortex areas
appear optimally placed, down to the limits of present computing resources.
If these types of results are confirmed, they constitute a predictive
success story of recent quantitative neuroanatomy.
This is a much
finer degree of neuro-optimality than previously reported (e.g., 3, 5, 6). We have also analyzed non-neural networks–-a benchmark computer
microchip, and macroeconomic patterns among U.S. states–-Aas a calibration of these methods, we have also analyzed layout of non-neural networks:
a benchmark computer microchip, and macroeconomic patterns among U.S.
states. Some chip layouts minimize connection costs
better than chance, but worse than the cortex layouts. The economic network performs even better than
the cortex, but apparently only via simple local processes.
Component placement optimization (also characterized as a quadratic assignment problem) has been a research focus in computer science for design of large-scale integrated circuits (8, 9). Briefly defined, the problem is: Given connections among a set of components, find the spatial layout of the components that minimizes total connection costs. This task, like many other network optimization problems (e.g., Travelling Salesman), is NP-hard (non-deterministic polynomial-time hard). The formal concept of NP-hardness, and the related concept of NP-completeness, need not be defined here (10, 11, 12); they have long been conjectured to be linked with a problem being intrinsically computationally intractable--i.e., not generally solvable without exhaustive search of all possible solution-candidates.
Of course, a cerebral cortex is vastly more complex than the 300-neuron C. elegans nervous system; it is also molded by experience much more extensively. And, even when connections are reported between two cortex areas, connection lengths and densities are usually not available. In addition, the two-dimensional cortical sheet is intricately folded, so that measuring distance between two areas becomes a three-dimensional problem. Observing the actual course of an axon bundle in the white matter is yet another layer of difficulty. Finally, widespread axonal bifurcation of corticocortical connections in cat and monkey visual systems has been reported, with estimates of branching ranging above 30% for some populations of projecting neurons (13). Such a bifurcation can save around 10% of the corresponding length of two separate connections (14, 4). However, cerebral connection compendia only describe links between pairs of areas (15, 16); they therefore cannot systematically represent these branchings, and so remain inaccurate as a basis for computing wirecosts. Is optimization still discernable through so many barriers?
Adjacency Rule Costing
The adjacency rule is, If two components a and b are connected, then a and b are adjacent. Two components are adjacent if immediately contiguous topologically (as are, e.g., U.S.A. and Canada). The rule is a candidate for a network wire-minimizing heuristic (17); in fact, it is also extensively confirmed for macaque and cat visual cortex areas, rat olfactory areas, and C. elegans ganglia (1, 2, 18, 19). Conformance of a cortex layout to such a "myopic" adjacency rule is much more feasible to compute than its total wirelength cost: Just compare interconnections and contiguities of the layout's areas, and score how many rule-violations occur. (For example, in Table 1 below, the seventh row "VOT" is {0, 2, 0, 2, 0, 1, 0}; it adds 2 to the total cost of the actual layout, since two areas are connected (i.e., value greater than 0) but not adjacent (i.e., not shaded).)
How useful would such adjacency costing be? The basic point remains, that component placement optimization is a computationally intractable, NP-hard problem; hence, a quick and dirty heuristic like the adjacency rule cannot provide a general solution to such a problem. (In fact, as noted elsewhere (18, 20), most of the worm's interganglionic connections are not to adjacent ganglia, but rather to more remote loci. Similarly for the majority of connections in macaque and in cat cortex (see Table S7).)
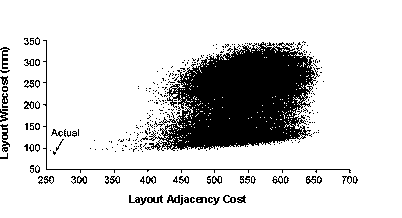
So a first question would be, How closely correlated here in fact are layout wirecosts and adjacency performance? As explained, we cannot expect to have accurate wirelength data for cerebral cortex. However, another strategy is to use our earlier C. elegans databases as a testbed for such queries; a positive picture for the worm would motivate exploring a similar working hypothesis for the cortex. In fact, the nematode layouts that perform best for the above simple adjacency rule also perform very well in terms of wirecost. This type of comparison can be generalized: Fig. 1 is a dispersion diagram for 100,000 randomly sampled worm ganglion layouts (21). The amorphous cloud of points indicates that, generally, adjacency rule conformance is not an efficient means to good wirecost. However, the narrow trail of points at the far lower left of the diagram suggests a special case: extremely good--near-optimal--adjacency rule performance does correlate well with very good wirecost. (See also Fig. 6 below.)
Fig. 1. Adjacency rule conformance, vs total wirecost, of 100,000 C. elegans ganglion layouts randomly sampled from the set of all 11! possible layouts (2). Correlation between adjacency rule performance and wirecost is not strong (r2 = 0.051); in general, the adjacency rule is not an effective means to good wirecost. However, the small set of layouts best fitting the adjacency rule--the points at the far left--behave markedly differently: they correspond closely to the best wirecost layouts. (The larger point at the far left represents the actual, minimum-wirecost layout.) Thus, good adjacency rule scores seem worth exploring as a surrogate for layout wirecost. (See Fig. S1.)
It should be noted that the scattergram shows that merely connecting components to their neighbors will not optimize wire cost; only a layout that is optimized in turn for adjacency rule conformance will do that. Hence, a regress: optimal wirecost can be approximated via optimal adjacency rule conformance, but now the wirecost minimization problem has been replaced by another combinatorial optimization problem of the same NP level of computational complexity (22). (In turn, adjacency optimization itself can be achieved via an evolutionary process such as a genetic algorithm--e.g., we have so implemented our GenAlg (23).) That the worm's connection matrix should be just such that the best adjacency rule layouts match the very cheapest wirecost ones--while the set of all others does not--may be an instance of the type of connection matrix finetuning we reported earlier (23) for a force-directed placement algorithm, i.e., that the worm's set of connections appears to be just such that it has relatively few local minima traps.
Size Law
So, the first provisional conclusion is that very good adjacency performance
is indeed worth examining as a feasible, surrogate index of connection-optimization
for layout of cortical areas. Another difficulty is that cortical connection and adjacency information
is not complete: For macaque (15)
and cat (16), the anatomy is most satisfactory
for the visual areas, usable also for auditory and somatosensory areas, but
only partial for frontal-limbic areas. Therefore,
any near-term optimization analysis of the cortex will not include the entire
system, but only large subsets. On the working hypothesis that the total system was perfectly optimized,
what level of optimization would be expected for such a subset? To begin with, the following Size Law can be
conjectured:
If a set of connected components is optimally placed, then, the smaller a subset of the total layout, the less optimal it will tend to be.
The idea of a proof begins with the familiar observation, that global optimality need not yield local subsystem optimality; local means-ends sacrifices are often required for the best overall solution. Furthermore, as an isolated subset of the total optimized system gets smaller, its own constraints (e.g., local-global tradeoffs) will be likely to depart more and more from those of the total layout, and so the subset by itself is less likely to be as well optimized. However, not all types of optimized networks obey such a Size Law: For instance, a uniform fabric mesh with just a regular, repeating pattern of connections between adjacent nodes--such as among wire intersections in chainlink fencing--will show perfect adjacency-rule optimization for all sizes of subsets. (See Fig. 2.)
Typical connection costs to be minimized are total wirelength, or violations of an adjacency rule. For an n-component layout, there are n! possible layouts. Optimality of a given layout can be expressed in terms of the percentile rank of its cost relative to all other alternative layouts, i.e., the proportion of all layouts that have a lower cost.
![]() A B
A B
Fig. 2. Global vs local optimization. A simple illustration that
connection-minimization of a total system does not entail
connection-minimization of its subsets:
Total system here consists of a 1-dimensional array of movable
components, 1 - 3, with fixed edge-terminal (vertical bar) at left. All connections are of equal cost per unit
length, (horizontal
only). Besides internal connection 2-3, 1 and 2 go
to left edge. (A) A globally optimal layout (cost: 4). However, if the system-subset is restricted to only components 2
and 3 with their outgoing connection to left edge, then the 2 and 3 layout is
(locally) suboptimal (cost: 3), compared with a layout with positions of 1, 2,
and 3 swapped (cost: 2), as in (B). In
contrast, the complete (B) layout is
locally optimal for subsystem 2 and 3, but at the expense of a
higher cost for the total layout (cost: 5).
How do neural systems behave? The Size Law can first be evaluated for the
11-component worm ganglion system, with total layout wirelength as the costoptimality measure. A nested chain of ganglion subsets was generated,
each composed of contiguous elements, proceeding from head to tail, from 4
to the full 11 components. The cost
of each subset of the actual layout was compared with all possible alternative
layouts of that subset of components. (Components
external, but immediately contiguous, to a subset are included in the analysis
as fixed "edge" constraints.) For the smallest set, 8.33% of all layouts
are better than the actual layout; this performance monotonically improves,
up to the full 11-component set, for which (as reported earlier (2,
24)) no layout is better than the actual one.
In addition, when optimality--proportion of layouts better than actual--is
plotted logarithmically against subset size, the descending curve closely
approximates a straight line (r2 > 0.99, p <
.001), suggesting the growth function is in fact a simple exponential one.
Mammalian cortex optimization is of at least as much interest as worm ganglion optimization. Yet, as explained, connection length data are not in general available, and even in the best cases (macaque and cat), adequate information on connections and adjacencies mainly exists for sensory areas. In addition, there is the double-bind that, according to the Size Law, component sets that are large enough to be well-optimized will tend to be too large for feasible search of all layouts. We first evaluated the Size Law for 17 contiguous core visual areas of macaque cortex (see Fig. 3), with conformance to the adjacency rule as optimality measure. For the macaque visual cortex areas, we constructed a matrix of ipsilateral intracortical connections, and a topological database of adjacencies among the areas (15, 26). Areas outside of the core set, but along the immediate periphery of the group, were treated again as fixed edge components. See Table 1. A nested series of compact subsets was generated, each composed of contiguous elements. While actual cortical areas form a jigsaw puzzle of widely differing sizes and shapes, they are approximated here as uniformly interchangeable: For example, when V1 and V2 are swapped, V1 adjacencies are assigned to V2, and vice versa, while V1 and V2 each retain their original connections. (Thus, as also to a lesser extent for the worm ganglion problem, actual cortical layouts are in fact even being tested against some topologically impossible alternative layouts.)
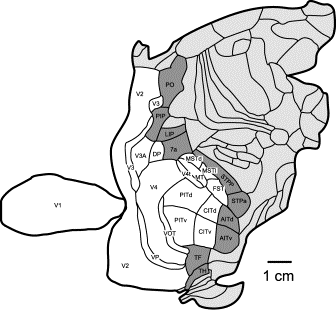
Fig. 3. Parcellation of macaque cerebral cortex.
Connection-cost optimization analysis of layout of 17 core areas of
the visual cortex (white), along with 10 immediately contiguous "edge"
areas (dark gray): Placement of the interconnected functional
areas is evaluated for how well total interconnection costs are minimized. 120 connections are reported among the core
areas and with the edge areas. Core
and edge areas are listed in Table 1 connection matrix
below. Rostral is to right. (See Fig.
S2.) After Felleman and Van Essen (15, 25);
areas MIP and MDP have been included in PO.
Table 1. Combined
connection and adjacency matrix for macaque visual cortex.
The series of 17 core visual areas shown above in Fig.
3 are listed (V1 - CITv), in the order in which they are successively
added to the analysis. They are followed by the set of 10 edge areas
for the total core (PO - TH). Connections
of an area to itself are excluded. A cell with 0 indicates no known connection between the area of
that row and of that column; 1 indicates connection in one direction between
the two areas; 2 indicates two-way connection.
Shaded cell
values designate topological contiguity of the two areas on the cortex sheet,
as in Fig. 3 (26, 27).
(See Table
S1.) (Adjacencies from Felleman
and Van Essen (see note 15).
Adjacencies do not include "diagonals", where only corners
of two areas are contiguous (e.g., V3a and LIP in Fig. 3); similarly for all
analyses below. (Because of incomplete information, the macaque
visual cortex edgering has a gap at PS, 29, 30.))

Fig. 4A shows that the Size Law seems to apply well to the actual cortex layout, and does not hold for a corresponding scrambled calibration set. The logarithmic scale of the y-axis should be noted: the Size Law curve fits a straight line well (r2 > 0.91, p < .001), suggesting, as for the much more complete worm ganglia subset series, a simple exponential growth function. It should be emphasized that the "total set" here consists of only 17 components of the entire ~73 area macaque cortical system, and does not include extracortical efferent and afferent connections. The Size Law provides an account of how such an incomplete system would only attain an optimality ranking in the top 10-7 of all possible layouts, even if the complete system were in fact perfectly optimal.
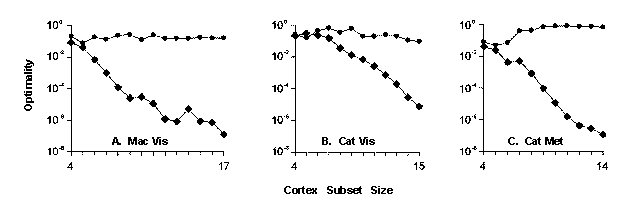
Fig. 4. Size Law for cortex areas. In each case, a series of nested compact subsets of the set of cortical areas was generated, each consisting of from 4 to the full set of areas. Each subset of the actual layout was compared with all possible alternative layouts of that subset for optimality; optimality-measure is conformance of the system to the adjacency rule (2). (16 and 17-element sets were each compared only with random samples of 109 alternative layouts.) (A) The system of components is 17 contiguous macaque visual cortex areas as in Fig. 3, with connections and adjacencies as in Table 1, and order of successive elements added as in Table 1. (B) Similar analysis for 15 cat visual cortex areas. (C) 14 cat cortex "metamodules" composed from 40 Brodmann areas of visual, auditory, and somatosensory regions. (See Figs. S3, S5, S6.)
In each case, the actual layout curve (diamonds) shows that smaller subsets rank approximately in the middle of their group of alternative layouts. But, as subset size increases, optimality-ranking of the actual layout consistently improves (with 1 or 2 exceptions in each series, p < 0.02). E.g., for macaque, fewer than one in a million of all alternative layouts conform to the adjacency rule better than the actual layout of the complete macaque set. For comparison, each scrambled layout curve (circles) shows the corresponding analysis for layouts of the areas with their adjacencies randomly shuffled; no Size Law trend toward improving optimality is now evident.
We similarly analyzed placement optimization for all 15 contiguous visual areas of cat cortex (along with a fixed edge zone of immediately surrounding areas) (Fig. S4). From published anatomy (16, 28), we constructed a matrix of cat ipsilateral intracortical connections and a topological database of adjacencies among the Brodmann areas. (Area SVA is included in 17, ALG in 19; DP in EPp & AI, V in VP & AII, SSF in EPp; some boundary indeterminacies remain unresolved.) (See Table S2.) The results (Figs. 4B, S5) confirm the picture for macaque visual cortex: Again, there is a significant Size Law effect, with smaller subsets of the actual layout ranking only in the midrange among all possible layouts, but larger subsets performing progressively better in their relative ranking for adjacency rule optimality. Optimality improves exponentially with subset size.
Naturally, these two visual cortex series raise the question of how much finer optimality even larger subsets of the actual layout attain: For instance, as observed via simple random samples of the extremely large total sets of all alternative possible layouts (29, 30). For cat sensory cortex (visual, auditory, and somatosensory), anatomical data for 39 contiguous Brodmann areas was adequate for such an analysis. When the subset was extended from the above visual 15 to 20 areas, a sample of a billion out of all possible 1018 layouts showed a rise of actual layout rank from 10-5 into the top 10-8 of all layouts. (That is, only 3 layouts out of a billion sampled were better than the actual layout.) For a 25-area subset, a billion-layout random sample yielded no placements cheaper than the actual one, suggesting the actual layout's ranking may be too high to be detectable at this sample size. Similarly no layouts cheaper than the actual one were found for 30 areas, and also up to 39. While this is of course the most striking finding reported here, it should be interpreted with some care; to begin with, larger sample sizes are warranted. For the 39 area cat cortex layout, we performed three separate random samplings, each of 100 billion layouts from the 1046 alternative possible layouts: we found no layouts with better adjacency-rule optimization than the actual one. However, with only 39 of the total 57 areas included in this analysis, the Size Law would suggest the 39 areas need not be perfectly optimally laid out, even if the total 57-component system were. (In addition, of course, the neuroanatomical database inevitably still includes errors.) We therefore constructed a simple genetic algorithm, along lines of one we had developed for the worm ganglion placement problem (23); it quickly finds layouts of the 39 areas cheaper than the actual one.
Metamodule Grouping
Of course, exhaustive search of all 57! alternative layouts of the 57 Brodmann areas of cat cortex (= 4 x 1076 layouts) would be cosmically unfeasible (2, 24). Another sampling strategy is instead to unite and conquer: Cluster the Brodmann areas of the actual layout into groups of topologically contiguous components, then search the smaller set of alternative placements of these locked-down "meta-modules" (see Table S3). This strategy is based upon a Metamodule Conjecture:
If a set of connected components is optimally placed, then a set of metamodules, each consisting of a subset of those components in the same positions, is also optimally placed.
Figs. 4C (and S6) show Size Law optimization performance of a series of nested layouts of 14 metamodules composed of 40 cat cortical areas. Each metamodule was grouped from adjacent Brodmann areas, all of the same modality (visual, auditory, then somatosensory); metamodules were assembled to have approximately equal numbers of areas, to be of approximately equal area, and to be each as compact as possible. The main observation is that the full 14 meta-module layout now approaches the top ten-millionth level of optimization--comparable to that found for the worm ganglion system. The Size Law curve again fits a straight line well (r2 > 0.97, p < .001). The consistency of the entire Size Law trend here constitutes further convergent support for the basic cortical optimality conclusion.
Non-Neural Networks
As a further calibration of the methods here, we analyzed connection optimization of two types of non-neural systems: a computer microchip, and macroeconomic commodity-flow networks. The chip was AMI49, the largest of the set of MCNC microcircuit benchmarks (31), which contains 49 blocks or modules--comparable to the number of functional areas in one cortex hemisphere. We studied three AMI49 layouts of fully automatic design, with costs to be minimized: (a) a function of layout area and maximum path delay (32); (b) a “blended” function of area and total wirelength (33); (c) total wirelength (34). (See Figs. 5, S7.) In each case, the central 15 blocks of the chip, along with the surrounding edge-zone of immediately contiguous blocks, was analyzed (see Table S4). Again, placement of the interconnected areas was evaluated for how well total interconnection costs--adjacency rule violations--are minimized, with the actual layout compared with alternative possible layouts. The Size Law curve for the minimum-wirelength layout (c) showed the same pattern as for the cortex networks, although somewhat weaker; the full 15 component subset attains an optimality-rank of 10-3 (see Figs. 6, S8). Neither of the other AMI49 layouts showed a Size Law pattern, nor did either attain significant optimality. (In comparisons with the cortex, it should be recalled that--unlike for chips--information on cortex wiring is still not complete.) So, for these calibration networks, adjacency rule conformance seems capable of distinguishing a target of wirelength minimization from some other related cost-measures. And again, as for the scrambled layouts earlier, adjacency costing does not seem to inflate optimality rankings. (See also Figs. 1 and 2 above.)
![]()
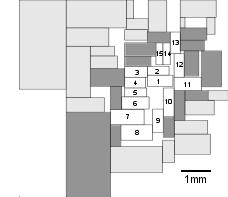
Fig. 5. Integrated circuit network for calibration of optimality analysis: AMI49 microchip, the largest of the MCNC set of benchmark circuits, with 49 modules (31). Lin and Chang layout; cost to be minimized is total wirelength (34). The central 15 blocks (white), along with the surrounding edge-zone of immediately contiguous blocks (dark gray), were analyzed. Again, placement of the interconnected areas is evaluated for how well total interconnection costs--adjacency rule violations--are minimized. (See Figs. S7, S8, Table S4.)
Fig. 6. Size Law for three layouts of AMI49 chip. In each case, the system of components is 15 contiguous central blocks, as in Fig. 5 (connections and adjacencies for Lin and Chang are as in Table S4). Optimality-measure is conformance of the system to the adjacency rule, with a layout scored in terms of its number of “all or nothing” violations. A series of nested compact subsets of the set of blocks was generated, each consisting of from 5 to the full 15 areas. Each subset of the actual layout was compared with all possible alternative layouts of that subset for adjacency-rule optimality (14 and 15-element sets were each compared only with random samples of 109 alternative layouts). The curve for the Lin and Chang (34) layout (C) shows a similar but weaker Size Law trend as the cortex networks earlier; the full 15-component subset only attains an optimality-rank of 1.5 x 10-3. Both the Esbensen and Kuh (32) layout (A), and the Hong et al (33) layout (B), show no Size Law pattern.
The macroeconomic system studied was U.S. states (see Fig. S9). The "connection"-cost to be minimized was combined "export + import" commodity flow (in U.S. $) between non-adjacent units. (Since nearly all cells in the matrices have non-0 values, economic transactions above a threshold were analyzed, with cutoff set here to yield approximately the same connectivity density as for macaque and cat cortex above; see Table S7.) Optimality-measure was conformance of the system to the simple "all or nothing" adjacency rule, with each layout scored in terms of its number of violations of the rule. For U.S. interstate commodity flow, a core of 15 central contiguous states, along with a surrounding edge-zone of immediately contiguous states, was analyzed (35) (see Table S5). We similarly analyzed as pilot data European international commodity flow among 8 countries (36). The total US system attains perfect connection-optimization. The smaller European nation set shows a similar pattern. (See Fig. S10.) As calibration, a scrambled layout of the U.S. system shows no optimization. This powerful performance of the optimization model (rather than a mere satisficing model) may appear to vindicate the wisdom of the hive, the "invisible hand" of laissez-faire economics. Indeed, very fine component placement optimization may thereby seem a rather pervasive phenomenon. However, each macroeconomic series completely departs from the Size Law pattern; in particular, smaller subsets already attain perfect optimality, with no alternative layouts better than the actual one. So, optimality does not necessarily entail conformance to the Size Law. This breakdown suggests the macroeconomic networks are only optimized via local processes, unlike the cortex (and some chip) networks. In contrast, conformance of the cortex systems to the Size Law suggests they are instead "high-tradeoff" networks requiring longrange micro/macro exchanges of local optimality for global optimality.
* * *
For each cortical network above, the population distribution of costs of alternative possible layouts conforms well to a normal distribution. For each neural system, when connections to/from surrounding edges are excluded from the analysis, optimality of the actual layout decreases. Conversely, when weighting information on connection strength is included in the adjacency-rule costing, actual layout optimality improves over simple all-or-nothing costing. Similarly for r2 fit to the Size Law. On an assumption that the more realistic the modeling, the more optimal a network should appear, these trends further confirm the optimality assessment.
The convergent set of "best of all possible brains" results reported here (see Table S6) raises the issue, Are complete mammal cortex layouts in fact optimal, as the total C. elegans ganglion layout appears to be? As for minimum-volume neuron arbors (4), optimal cortex may be just an initial plan that can be modified and elaborated. Natural next questions arise about optimization mechanisms, for instance, direction of causation--from connections to positioning, or vice versa, or both. Although the point should be interpreted with some care, each of the cortex systems analyzed here shows better goodness of fit to an "If connected, then adjacent" hypothesis than to the converse hypothesis. (The test consists of comparing, for each actual layout (see Table S7), its number of counterexamples to “If connected, then adjacent” with the number of counterexamples to the converse hypothesis; the comparison includes a correction for unequal populations of connections and adjacencies. The scrambled calibration layouts show no bias in either direction.) It is also worth noting that, for the C. elegans optimization problem, we have demonstrated simple mechanisms that proceed solely from connections to adjacencies--namely, a genetic algorithm, and also a force-directed placement algorithm (23). A similar genetic algorithm was described above for cat sensory cortex.
This discussion has focussed upon neuroanatomy, upon minimization of biological connection-structures. However, the above macroeconomic analyses really concerned abstract, functional "connections"--i.e., commercial transactions. We thereby proceed from anatomy to physiology broadly conceived. The adjacency rule then generalizes, If components are "connected" in the wider sense of causal interrelation, then they are topologically adjacent. (No action at a distance.) For instance, the large-scale optimization landscapes of cortex and genome may be worth comparing: the structure of the genome would be analyzed similarly as above. Two genes might count as "connected" if they are co-activated--(approximately) contemporaneously expressed. Contiguity would be interpreted as proximity of position in the 3-d genome structure. In fact, a first step already towards such an approach may be recent studies of clustering of highly expressed genes in chromosomal domains (37).
Acknowledgements: NIMH grant MH49867 supported this work. NCI generously made available supercomputers at the Advanced Biomedical Computing Center. We are indebted to Richard Kissh for parallel supercomputer software engineering. We are also grateful for assistance of Eric Celarier, Jarrett Rosenberg, and Thomas Schaefer.
Historical note: The material in this report first appeared in a February 2000 NIMH grant proposal (7). The present draft was submitted for publication in Proceedings of the National Academy of Sciences on December 21 2002; consequently, it contains no references to work submitted or appearing after this date. The present draft was communicated to PNAS on September 1 2003. This material was presented at: Workshop on Optimization and Constraints in Evolution of Brain Design, Cold Spring Harbor Laboratory, July 14, 2003; Workshop on Constraints in Neural Systems Design, Computational Neuroscience Meeting CNS*03, Alicante, July 2003; and the Philosophy, Neuroscience, and Psychology Colloquium, Washington University, October 9, 2003.
References
1. Cherniak, C. (1991) Component placement optimization in the brain. University of Maryland Institute for Advanced Computer Studies Technical Report, No. 91‑98 / CS-TR-2711 www.cs.edu/Library/TRs/
2. Cherniak, C. (1994) Component placement optimization in the brain. J. Neurosci. 14, 2418-2427.
3. Mitchison, G. (1992) Axonal trees and cortical architecture. Trends Neurosci. 15, 122-126.
4. Cherniak, C., Changizi, M. & Kang, D. (1999) Large-scale optimization of neuron arbors. Phys. Rev. E 59, 6001-6009. http://link.aps.org/abstract/PRE/v59/p6001
5. Ramon y Cajal, S. (1995) Histology of the Nervous System of Man and Vertebrates, trans. Azoulay, L., Swanson, N., Swanson, L. (Oxford, New York), Vol. 1, p. 116.
6. Weibel, E., Taylor, C. & Bolis, L., eds. (1998) Principles of Animal Design (Cambridge, New York).
7. Cherniak, C. (2003) Network optimization in the brain [II, 2000]: Cerebral cortex layout. University of Maryland Institute for Advanced Computer Studies Technical Report, UMIACS-TR-2003-93 / CS-TR-4525. www.cs.edu/Library/TRs/
8. Kuh, E. & Ohtsuki, T. (1990) Recent advances in VLSI layout. Proc. of the IEEE 78, 237‑263.
9. Sherwani, N. (1999) Algorithms for VLSI Physical Design Automation, 3rd ed. (Kluwer, Boston).
10. Garey, M. & Johnson, D. (1979) Intractability: A Guide to the Theory of NP‑Completeness (W.H. Freeman, San Francisco).
11. Lewis, H. & Papadimitriou, C. (1978) The efficiency of algorithms. Sci. Am. 238, 96‑109.
12. Stockmeyer, L. & Chandra, A. (1979) Intrinsically difficult problems. Sci. Am. 240, 140‑159.
13. Bullier, J. & Kennedy, H. (1987) Axonal bifurcation in the visual system. Trends Neurosci. 10, 205-210.
14. Hwang, F., Richards, D. & Winter, P. (1992) The Steiner Tree Problem (North-Holland, Amsterdam) 37-49.
15. Felleman, D. & Van Essen, D. (1991) Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1‑47. (Fig. 2, p. 4.)
16. Scannell, J., Blakemore, C. & Young, M. (1995) Analysis of connectivity in the cat cerebral cortex. J. Neurosci. 15, 1463-1483. (Fig. 1, p. 1466; with corrections.)
17. Soukup, J. (1981) Circuit layout. Proc. IEEE 69: 1281-1304.
18. Cherniak, C. (1995) Neural component placement. Trends Neurosci. 18, 522-527.
19. Young, M. (1992) Objective analysis of the topological organization of the primate cortical visual system. Nature 358, 152-155.
20. Cherniak, C. (1996)
Reply to Letter to Editor. Trends Neurosci.
19, 414-415. www.wam.umd.edu/~cherniak/
21. See supplementary material: University of Maryland Institute for Advanced Computer Studies Technical Report UMIACS-2003-103 / CS-TR-4535. www.cs.umd.edu/Library/TRs/
22. The 2-d adjacency-rule placement problem is NP-complete: It can be efficiently reduced to Hamiltonian Path (see reference 10, problem GT39). Personal communication, Thomas Schaefer.
23. Cherniak, C., Mokhtarzada,
Z. & Nodelman, U. (2002) Optimal-wiring models of neuroanatomy. In Computational Neuroanatomy: Principles and
Methods, ed. Ascoli, G. (Humana,
Totowa, NJ) 71-82.
24. Cherniak, C. (1994)
Philosophy and computational neuroanatomy. Philos. Studies 73, 89-107.
25. Van Essen, D. et al. (1990) Modular and hierarchical organization of extrastriate visual cortex in the macaque monkey. Cold Spring Harbor Symp. Quant. Biol. LV, 679-696. (Fig. 6, p. 689.)
26. Connections based upon: Scannell, J. (1997) Determining cortical landscapes. Nature 386, 452. www.psychology.ncl.ac.uk/jack/gyri.html ; from (27).
27. Young, M. (1993) The organization of neural systems in the primate cerebral cortex. Proc. R. Soc. Lond. B Biol. Sci. 252, 13-18.
28. Rosenquist, A. (1985) The organization of neural systems in the primate cerebral cortex. In Cerebral Cortex, eds. Peters, A. & Jones, E., vol. 3. (Plenum, New York) 81-117.
29. Golden, B. & Stewart, W. (1985) Empirical analysis of heuristics. In The Traveling Salesman Problem, eds. Lawler, E. et al. (Wiley, New York), 207-249.
30. Bentley, J. (1990) Experiments on traveling salesman heuristics. Proc. ACM-SIAM Symp. Discrete Algorithms (San Francisco) 91-99.
31. Connection matrix of AMI49: Benchmark suite LayoutSynth92 May 1992 International Workshop on Layout Synthesis, Research Triangle Park, NC. www.cbl.ncsu.edu/pub/Benchmark_dirs/LayoutSynth92/bench90.tar.Z
32. Esbensen, H. & Kuh, E. (1997) A performance-driven IC/MCM placement algorithm featuring explicit design space exploration. ACM Trans. Design Automat. Electron. Systems, Vol. 2, no. 1, Fig. 9(b), p. 79. http://info.acm.org/todaes/V2N1/L134/paper.pdf
33. Hong, X., Huang, G., Cai, Y., Dong, S., Cheng, C. & Gu, J. (2000) Corner block list: An effective and efficient topological representation of non-slicing floorplan. Int. Conf. Computer-Aided Design (IEEE, San Jose, CA) 8-12. www.cse.ucsc.edu/research/surf/GSRC/Papers/01a_2.pdf
34. Diagram based upon: Lin, J.-M. & Chang, Y.-W. (2001) TCG: A transitive closure graph based representation for non-slicing floorplans. Proc. ACM/IEEE Design Automation Conf. (June 18-22, 2001, Las Vegas, NV) Figure 6 (2). http://cc.ee.ntu.edu.tw/~ywchang/Papers/tcg01.ps
35. State-to-State Commodity Flows: Commodity Flow Survey (1997). Bureau of Transportation Statistics, U.S. Department of Transportation. www.bts.gov/ntda/cfs/docs/cf97odv.html
36. International Trade
by Commodity Statistics (1999). Organisation
for Economic Co-operation and Development(Boulogne, France). www.oecd.org/xls/M00017000/M00017616.xls
37. Caron, H. et al. (2001) The human transcriptome map: Clustering of highly expressed genes in chromosomal domains. Science 291, 1289-1292.
Supporting Online Material:
www.cs.umd.edu/Library/TRs/CS-TR-4535/CS-TR-4535.pdf
Figures S1 to S10, Tables S1 to S7