 Homework Assignment 4
Homework Assignment 4
 Homework Assignment 4
Homework Assignment 4
Due: May 1, 2006.
This assignment will give you practice at writing Java programs that create and manipulate objects.
Problem 4.1.
As shown in Figure 1 below, rectangles may be defined by the (x,y) coordinates of corner points that are diagonally opposite.
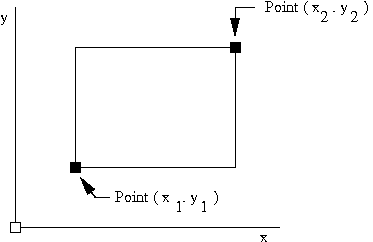
Figure 1. Definition of a rectangle via diagonally opposite corner points
With this definition in place, the following script of code is a very basic implementation of a class for creating and working with rectangle objects.
/*
* ==========================================================================
* Rectangle.java : A library of methods for creating and managing rectangles
*
* double area() -- returns the area of a rectangle
* double perimeter() -- returns the perimeter of a rectangle
*
* Written By : Mark Austin November 2005
* ==========================================================================
*/
import java.lang.Math;
public class Rectangle {
protected double dX1, dY1; // Coordinate (x,y) for corner 1....
protected double dX2, dY2; // Coordinate (x,y) for corner 2....
// Constructor methods ....
public Rectangle() {}
public Rectangle( double dX1, double dY1, double dX2, double dY2 ) {
this.dX1 = dX1; this.dY1 = dY1;
this.dX2 = dX2; this.dY2 = dY2;
}
// Convert rectangle details to a string ...
public String toString() {
return "Rectangle: Corner 1: (x,y) = " + "(" + dX1 + "," + dY1 + ")\n" +
" Corner 2: (x,y) = " + "(" + dX2 + "," + dY2 + ")\n";
}
// ====================================
// Compute rectangle area and perimeter
// ====================================
public double area() {
return Math.abs( (dX2-dX1)*(dY2-dY1) );
}
public double perimeter() {
return 2.0*Math.abs(dX2-dX1) + 2.0*Math.abs( dY2-dY1 );
}
// Exercise methods in the Rectangle class ....
public static void main ( String args[] ) {
System.out.println("Rectangle test program ");
System.out.println("===========================");
// Setup and print details of a small rectangle....
Rectangle rA = new Rectangle( 1.0, 1.0, 3.0, 4.0 );
System.out.println( rA.toString() );
// Print perimeter and area of the small rectangle....
System.out.println( "Perimeter = " + rA.perimeter() );
System.out.println( "Area = " + rA.area() );
}
}
The script of program output is as follows:
Script started on Fri Apr 21 10:17:29 2006
prompt >>
prompt >> java Rectangle
Rectangle test program
===========================
Rectangle: Corner 1: (x,y) = (1.0,1.0)
Corner 2: (x,y) = (3.0,4.0)
Perimeter = 10.0
Area = 6.0
prompt >> exit
Script done on Fri Apr 21 10:17:39 2006
The Rectangle class has methods to create objects (i.e, Rectangle), convert the details of a rectangle object into a string format (i.e., toString), and compute the rectangle area and perimeter (i.e., area() and permieter(), respectively). The implementation uses two pairs of doubles ( dX1, dY1 ) and ( dX2, dY2 ) to define the corner points.
Suppose that, instead, the corner points are defined via a Vertex class, where
public class Vertex {
protected double dX, double dY
..... details of constructors and other methods removed ...
}
The appropriate modification for Rectangle is:
public class Rectangle {
protected Vertex vertex1; // First corner point....
protected Vertex vertex2; // Second corner point....
..... details rectangle removed ....
}
Fill in the missing details (i.e., constructors and toString() method) of class Vertex. Modify the code in Rectangle to use Vertex class. The resulting program should have essentially has the same functionality as the original version of Rectangle.
Hint. My implementation of Vertex is very short. It contains a couple of constructor methods and a toString() method. Just to be safe you could exercise these methods by writing a short main() method.
Problem 4.2.
There are lots of problems in engineering where the position of point needs to be evaluated with respect to a shape. Evaluation procedures can be phrased in terms of questions. For example, is the point inside (or outside) the shape?; Does the point lie on the boundary of the shape?; Does the point lie above/below the shape? Does the point lie to the left or right of the shape?; How far is the point from the perimeter?
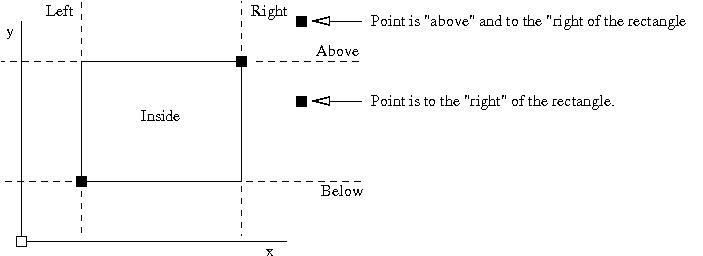
Figure 2. Classification of an (x,y) cooordinate relative to a rectangle
Figure 2 illustrates these ideas for one of the simplest cases possible, one point and a rectangle. Extend the functionality of the Rectangle class so that the possition of a point can be evaluated with respect to a specific rectangle object.
The appropriate method declarations are as follows:
public boolean isInside ( Vertex v ) { ... }
public boolean isOutside ( Vertex v ) { ... }
public boolean isOnPerimeter ( Vertex v ) { ... }
public boolean isAbove ( Vertex v ) { ... }
public boolean isBelow ( Vertex v ) { ... }
public boolean isLeft ( Vertex v ) { ... }
public boolean isRight ( Vertex v ) { ... }
If the (x,y) coordinates of a vertex are inside a particular rectangle, then the method isInside() should return true. Otherwise, it should return false. From Figure 2 it should evident that some points will result in multiple methods returning true. For example, points in the top right-hand side of the coordinate system will be outside, to the right, and above the rectangle.
Fill in the details of each method, and then develop a test program to exercise the procedures. Perhaps the most straight forward way of doing this is to write an extensive set of tests in the main() method for class Rectangle.
Problem 4.3.
The left-hand side of Figure 3 shows the essential details of a domain familiar to many children. One by one, rectangular blocks are stacked as high as possible until they come tumbling down -- the goal, afterall, is to create a spectacular crash!!
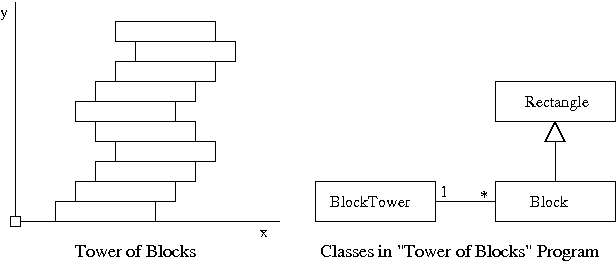
Figure 3. Visual Schematic and Classes for ``Tower of Blocks''
Suppose that we wanted to model this process and use engineering principles to predict incipient instability of the block tower. Consider the following observations:
The right-hand side of Figure 3 shows the relatioship among the classes. One BlockTower program (1) will employ many blocks, as indicated by the asterik (*).
Develop a Java program that builds upon the Rectangle class written in the previous questions. The class Block should store the density of the block (this will be important in determining its weight) and methods to compute the weight and centroid of each block. The BlockTower class will use block objects to build the tower.
A straight forward way of modeling the block tower is with an ArrayList. After each block is added, the program should conduct a stability check. If the system is still stable, then add another block should be added. The simulation should cease when the tower of blocks eventually becomes unstable.
Note. To simplify the analysis, assume that adjacent blocks are firmly connected.
Stability Considerations.
If the blocks are stacked perfectly
on top of each other, then from a mathematical standpoint the tower
will never become unstable. In practice, this never happens.
There is always a small offset and, eventually, it's the
accumulation of offsets that leads to instability.
For the purposes of this question, assume that blocks are five units wide and one unit high. When a new block is added, the block offset should be one unit. To make the question interesting, assume that four blocks are stacked with an offset to the right, then three blocks are added with an offset to the right, then four to the left, three to the right, and so forth. The tower will become unstable when the center of gravity of blocks above a particular level falls outside the edge of the supporting block.
Hint. To help you get started, here is a skeleton of source code:
/**
* =================================================================
* BlockTower.java: This java simulates assembly of the block tower.
*
* Written by: Mark Austin April 2006
* =================================================================
*/
import java.lang.Math;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
public class BlockTower {
public static void main( String args[] ) {
boolean TowerStable = true;
int offset = 0;
// Main loop for assembly of the block tower ...
int BlockNo = 1;
List blockList = new ArrayList();
while ( TowerStable == true ) {
// Compute incremental offset for i-th block .....
offset = (int) ( Math.floor ((BlockNo - 1)/5.0) + (BlockNo-1)%5 );
if ((BlockNo-1)%5 == 4 ) offset = offset - 2;
// Compute (x,y) coordinates of block vertices...
// ... details of source code removed .....
// Create new block ...
// ... details of source code removed .....
// Add block to tower ....
// ... details of source code removed .....
// Compute (x,y) coordinates of tower centroid ...
// ... details of source code removed .....
// Test for stability of tower ...
// ... details of source code removed .....
// Update parameters ....
BlockNo = BlockNo + 1;
}
// Print details of block tower ....
// ... details of source code removed .....
}
}
Computing the offset of the blocks is quite tricky (took me a couple of tries to get it right), so I am just leaving that part in the program. The abbreviated output is:
Add block 1
=========================
Total Mass =5.0
FirstMoment(X) =12.5
FirstMoment(Y) =2.5
Centroid(X) =2.5
Centroid(Y) =0.5
Tower of blocks is stable
.... details of output removed ....
Add block 14
=========================
Total Mass =70.0
FirstMoment(X) =350.0
FirstMoment(Y) =490.0
Centroid(X) =5.0
Centroid(Y) =7.0
Crash!!
Tower of 14 blocks is unstable
Details of Block Tower
================================
Block: Vertex(0.0, 0.0)
Vertex(5.0, 1.0)
density = 1.0
thickness = 1.0
area = 5.0
mass = 5.0
.... details of block tower removed ....
Block: Vertex(5.0, 13.0)
Vertex(10.0, 14.0)
density = 1.0
thickness = 1.0
area = 5.0
mass = 5.0
Answer. 14 blocks.
Note. For each problem, hand in a copy of your program source code and a script of I/O for typical program usage. To create a script, type something like:
prompt >> script output-file
Now all input/output on the screen will be echoed to the file "output-file". To terminate the script, type:
prompt >> exit
Now print "output-file" and hand it in.
Developed in April 2006 by Mark Austin
Copyright © 2006, Department of Civil and Environmental Engineering, University of Maryland